3.5圆周角定理
图片预览








文档简介
课件32张PPT。3.5 圆周角第1课时 圆周角定理【学习目标】
1.理解圆周角的概念;
2.掌握圆周角定理及其推论,并能熟练地运用其进行论证和计算;
3.通过圆周角定理的证明,了解分情况证明数学问题的思想方法.
【学法指导】
1.注意和垂径定理的联系;
2.证明时注意分类讨论和由特殊到一般的研究方法;
3.利用“直径所对的圆周角是直角”构造圆中的直角三角形.填 一 填
1.圆周角的概念
圆周角:顶点在圆上,它的两边都和圆相交,像这样的角叫做圆周角.【知识管理】注意:圆周角必须具备的两个条件:①顶点在圆上;②角的两边都与圆相交,二者缺一不可.圆心角与圆周角的相同点:角的两边都和圆相交.
不同点:圆心角的顶点在圆心,而圆周角的顶点在圆上.
2.圆周角定理
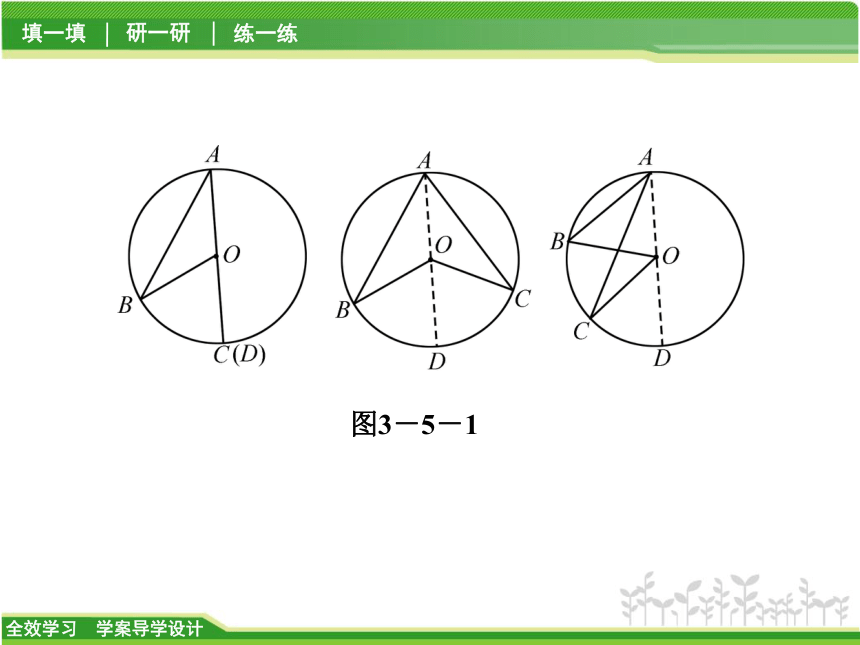
定理:圆周角的度数等于它所对的圆心角的一半.图3-5-13.圆周角定理的推论
定理:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
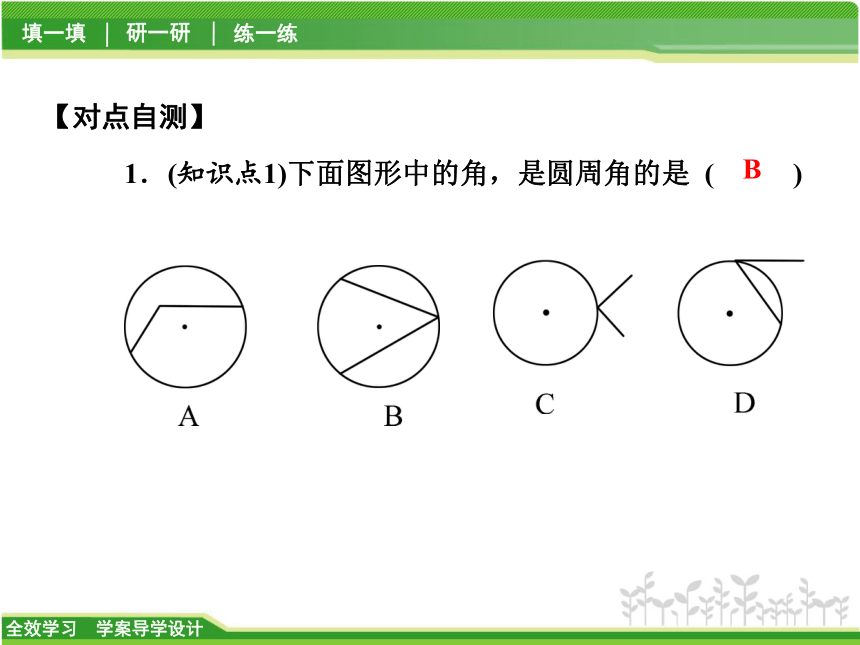
1.(知识点1)下面图形中的角,是圆周角的是 ( )【对点自测】B2.(知识点2)如图3-5-2所示,已知∠ACB是⊙O的圆周角,∠ACB=40°,则圆心角∠AOB是 ( )
A.40°
B.50°
C.80°
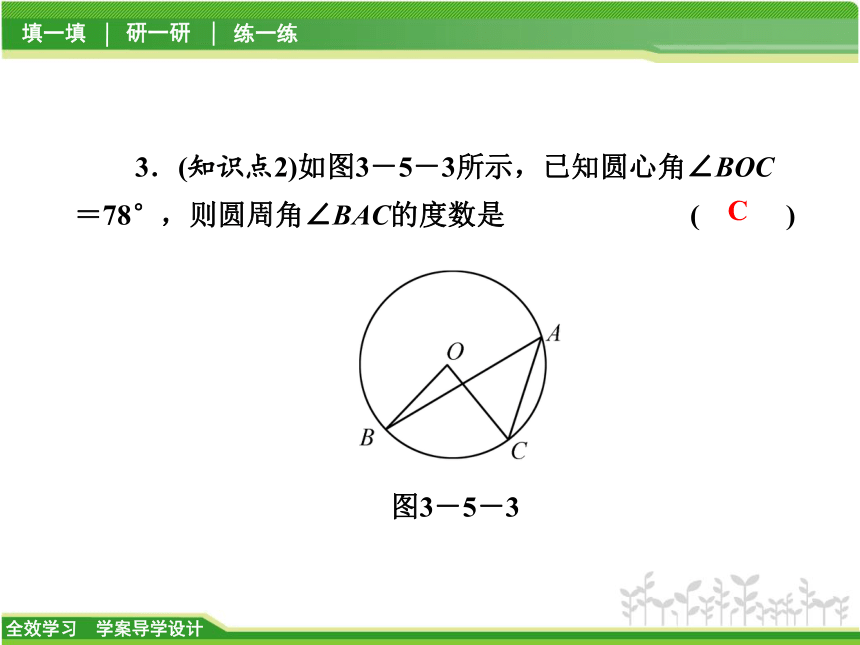
D.100°图3-5-2C3.(知识点2)如图3-5-3所示,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是 ( )图3-5-3CA.156°
B.78°
C.39°
D.12°
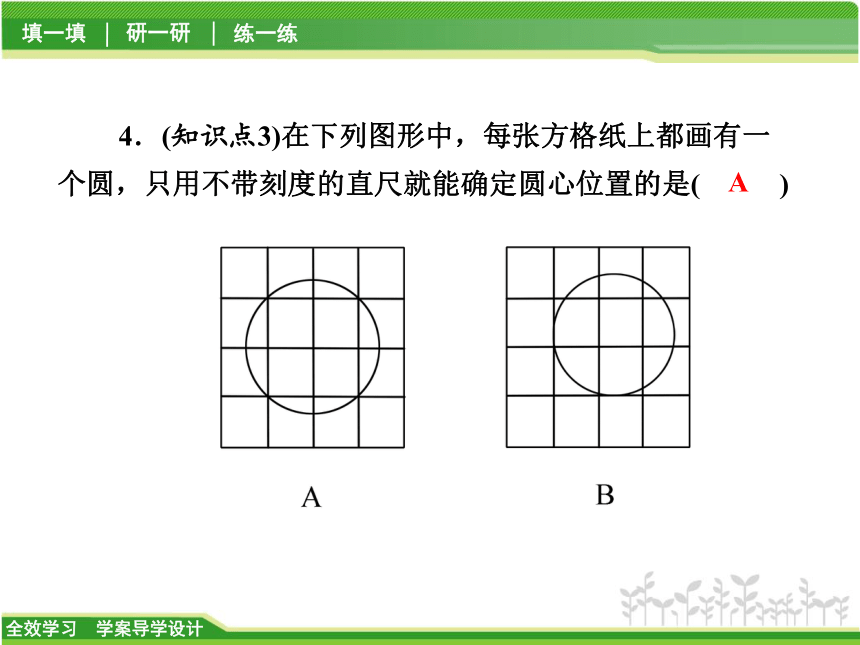
【解析】 同弧所对的圆周角等于它所对的圆心角的一半.4.(知识点3)在下列图形中,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( )A5.(知识点3)如图3-5-4,△ABC为⊙O的内接三角形,AB是直径,∠A=20°,则∠B的度数是 ( )
A.20° B.40°
C.70° D.160°图3-5-4C研 一 研类型之一 利用圆周角定理计算圆周角的大小
例1 如图3-5-5所示,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为 ( )图3-5-5AA.40°
B.30°
C.45°
D.50°【点悟】 找出同一条弧上的圆周角和所对的圆心角是解决此类问题的关键. 1.将量角器按如图3-5-6所示的方式放置在三角形纸板上,使点C在半圆上.点A,B处的读数分别为86°,30°,则∠ACB的大小为 ( )
图3-5-6BA.15°
B.28°
C.29°
D.34°2.如图3-5-7所示,已知点E是圆O上的点,B,C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为_________.图3-5-769°3.如图3-5-8所示,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是 ( )图3-5-8AA.25°
B.40°
C.30°
D.50°例2 如图3-5-9所示,弦AB把圆周分成1∶5的两个部分,那么弦AB所对的圆周角的度数是______________.图3-5-930°或150° 1.如图3-5-10所示,A,B,C,D四点都在⊙O上,∠BOC=110°,则∠BDC的度数为( )
A.110°
B.70°
C.55°
D.125°
图3-5-10D2.在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,这条弧所对的圆心角和圆周角的度数分别为________、_________.140°70°类型之二 利用圆周角定理的推论计算或证明
例3 如图3-5-11所示,已知AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?图3-5-11【解析】 连结AD,根据直径所对的圆周角是直角,得∠ADB=90°,然后由等腰三角形的性质得BD=CD.
解:BD=CD.理由是:连结AD.∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AC=AB,∴BD=CD.【点悟】 直径是构造直角的一个重要条件,一般是构造相关的弦,把直径所对的圆周角转化为90°的角,可以简单说成“有直径,造直角”. 1.如图3-5-12所示,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连结AD,则∠DAC的度数为________.
图3-5-1230°【解析】 因为AB为⊙O的直径,所以∠ADB=90°,又因为△ABC是等边三角形,所以AD是∠BAC的角平分线,所以∠DAC=30°.2.如图3-5-13,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.图3-5-13练 一 练
1.理解圆周角的概念;
2.掌握圆周角定理及其推论,并能熟练地运用其进行论证和计算;
3.通过圆周角定理的证明,了解分情况证明数学问题的思想方法.
【学法指导】
1.注意和垂径定理的联系;
2.证明时注意分类讨论和由特殊到一般的研究方法;
3.利用“直径所对的圆周角是直角”构造圆中的直角三角形.填 一 填
1.圆周角的概念
圆周角:顶点在圆上,它的两边都和圆相交,像这样的角叫做圆周角.【知识管理】注意:圆周角必须具备的两个条件:①顶点在圆上;②角的两边都与圆相交,二者缺一不可.圆心角与圆周角的相同点:角的两边都和圆相交.
不同点:圆心角的顶点在圆心,而圆周角的顶点在圆上.
2.圆周角定理
定理:圆周角的度数等于它所对的圆心角的一半.图3-5-13.圆周角定理的推论
定理:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
1.(知识点1)下面图形中的角,是圆周角的是 ( )【对点自测】B2.(知识点2)如图3-5-2所示,已知∠ACB是⊙O的圆周角,∠ACB=40°,则圆心角∠AOB是 ( )
A.40°
B.50°
C.80°
D.100°图3-5-2C3.(知识点2)如图3-5-3所示,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是 ( )图3-5-3CA.156°
B.78°
C.39°
D.12°
【解析】 同弧所对的圆周角等于它所对的圆心角的一半.4.(知识点3)在下列图形中,每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( )A5.(知识点3)如图3-5-4,△ABC为⊙O的内接三角形,AB是直径,∠A=20°,则∠B的度数是 ( )
A.20° B.40°
C.70° D.160°图3-5-4C研 一 研类型之一 利用圆周角定理计算圆周角的大小
例1 如图3-5-5所示,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为 ( )图3-5-5AA.40°
B.30°
C.45°
D.50°【点悟】 找出同一条弧上的圆周角和所对的圆心角是解决此类问题的关键. 1.将量角器按如图3-5-6所示的方式放置在三角形纸板上,使点C在半圆上.点A,B处的读数分别为86°,30°,则∠ACB的大小为 ( )
图3-5-6BA.15°
B.28°
C.29°
D.34°2.如图3-5-7所示,已知点E是圆O上的点,B,C分别是劣弧AD的三等分点,∠BOC=46°,则∠AED的度数为_________.图3-5-769°3.如图3-5-8所示,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是 ( )图3-5-8AA.25°
B.40°
C.30°
D.50°例2 如图3-5-9所示,弦AB把圆周分成1∶5的两个部分,那么弦AB所对的圆周角的度数是______________.图3-5-930°或150° 1.如图3-5-10所示,A,B,C,D四点都在⊙O上,∠BOC=110°,则∠BDC的度数为( )
A.110°
B.70°
C.55°
D.125°
图3-5-10D2.在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,这条弧所对的圆心角和圆周角的度数分别为________、_________.140°70°类型之二 利用圆周角定理的推论计算或证明
例3 如图3-5-11所示,已知AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD的大小有什么关系?为什么?图3-5-11【解析】 连结AD,根据直径所对的圆周角是直角,得∠ADB=90°,然后由等腰三角形的性质得BD=CD.
解:BD=CD.理由是:连结AD.∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AC=AB,∴BD=CD.【点悟】 直径是构造直角的一个重要条件,一般是构造相关的弦,把直径所对的圆周角转化为90°的角,可以简单说成“有直径,造直角”. 1.如图3-5-12所示,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连结AD,则∠DAC的度数为________.
图3-5-1230°【解析】 因为AB为⊙O的直径,所以∠ADB=90°,又因为△ABC是等边三角形,所以AD是∠BAC的角平分线,所以∠DAC=30°.2.如图3-5-13,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)若⊙O的半径为4,∠BAC=60°,求DE的长.图3-5-13练 一 练
同课章节目录
