3.5 圆周角定理的推论第2课时

课件35张PPT。第2课时 圆周角定理的推论【学习目标】
1．运用圆周角定理的推论进行计算；
2．运用圆周角定理的推论进行证明．
【学法指导】
1．利用在同一圆中同弧所对的圆周角相等，进行角与角之间的转化；
2．作出直径所对的圆周角(直角)是圆中最常用的方法．填 一 填
1．圆周角定理的另一推论
在同圆或等圆中，同弧或等弧所对的__________相等；相等的圆周角所对的______也相等．
2．圆内角、圆外角与圆周角的关系
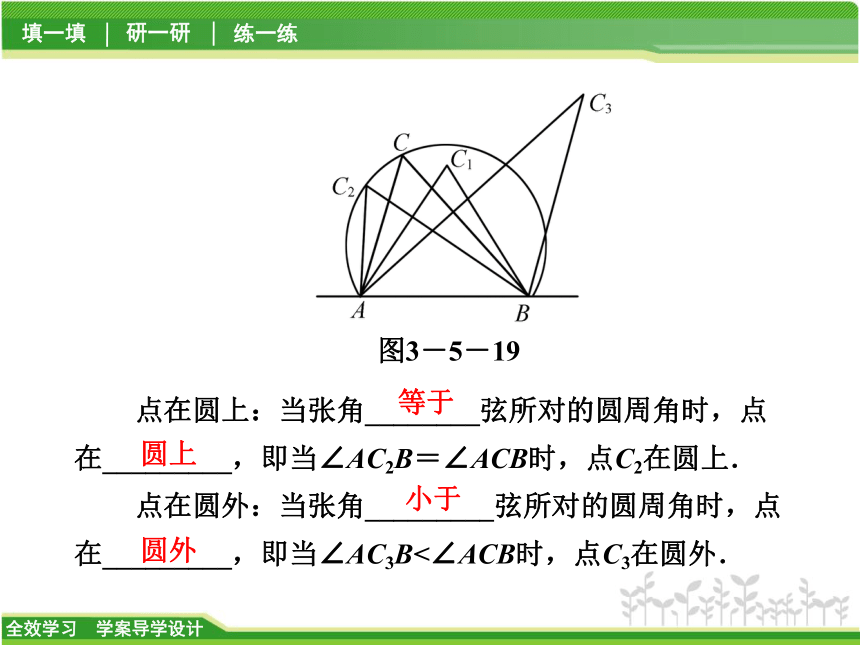
点在圆内：点位于弦所在直线的同侧的前提下，当点到弦的两端的张角_________弦所对的圆周角时，点在_________，即当∠AC1B>∠ACB时，点C1在圆内．(如图3－5－19所示)【知识管理】圆周角弧大于圆内点在圆上：当张角________弦所对的圆周角时，点在_________，即当∠AC2B＝∠ACB时，点C2在圆上．
点在圆外：当张角_________弦所对的圆周角时，点在_________，即当∠AC3B<∠ACB时，点C3在圆外．图3－5－19等于圆上小于圆外
1．(知识点1)如图3－5－20所示，⊙O中弦AB，CD相交于点E，连结BD，AC，BD＝AC，BE＝CE则图中相等的角共有 (　 　)【对点自测】图3－5－20BA．3对　　　　　　　　B．4对
C．5对 D．6对
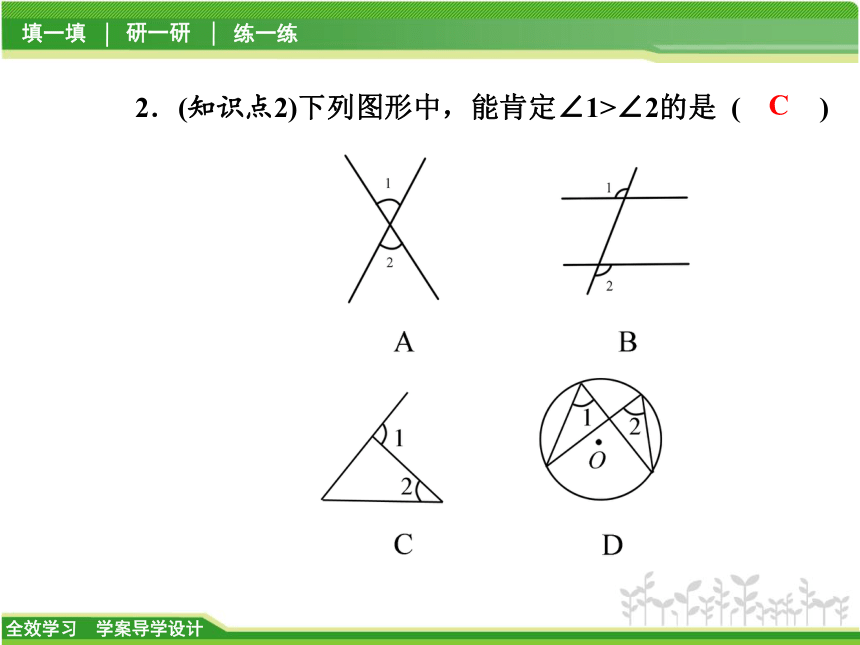
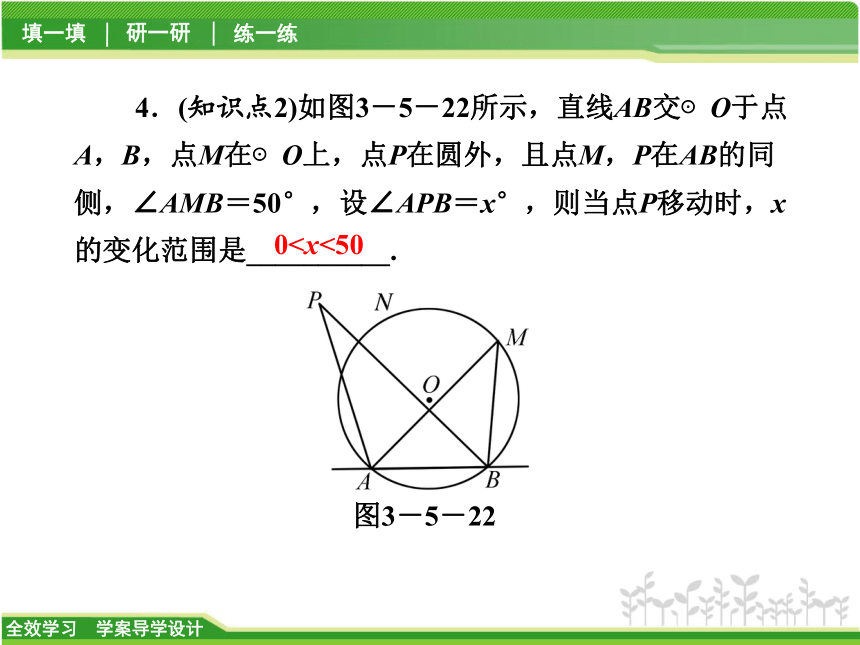
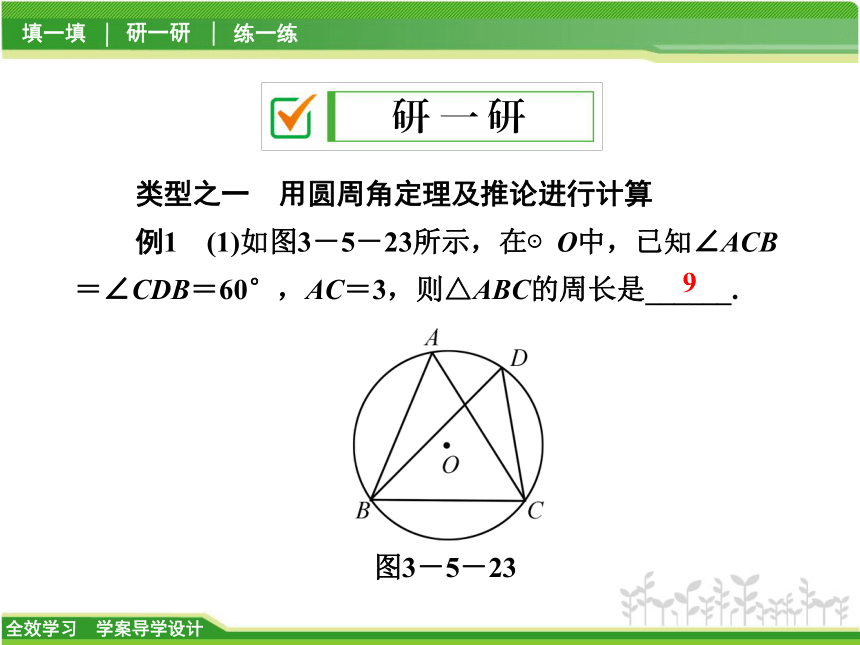
【解析】 ∠A＝∠D，∠B＝∠C，∠BED＝∠CEA，∠AED＝∠BEC，共4对．故选B.2．(知识点2)下列图形中，能肯定∠1>∠2的是 (　 　)C3．(知识点1)如图3－5－21所示，⊙O的直径CD过弦EF的中点G，∠EOD＝40°，则∠DCF＝__________.图3－5－2120°4．(知识点2)如图3－5－22所示，直线AB交⊙O于点A，B，点M在⊙O上，点P在圆外，且点M，P在AB的同侧，∠AMB＝50°，设∠APB＝x°，则当点P移动时，x的变化范围是__________.图3－5－220由∠ANB>∠P可得∠M>∠P，故0°<∠P<50°，即0例1　(1)如图3－5－23所示，在⊙O中，已知∠ACB＝∠CDB＝60°，AC＝3，则△ABC的周长是______.图3－5－239A．60°　　　　　　　B．120°
C．135° D．150°图3－5－24D【解析】(1)由同弧所对的圆周角相等得∠A＝∠D＝60°.再由∠ACB＝60°可得△ABC是等边三角形，故△ABC的周长为3×3＝9. 1.如图3－5－25所示，⊙O是正三角形ABC的外接圆，点P在劣弧AB上，∠ABP＝22°，则∠BCP的度数为_________.图3－5－25【解析】 ∠ACP＝∠ABP＝22°，∠BCP＝60°－22°＝38°.38°2．如图3－5－26所示，△ABC内接于⊙O，∠C＝30°，AB＝2，则⊙O的直径为 (　 　)图3－5－26D【点悟】 “作直径，造直角”，把一般三角形转化为直角三角形是解题常用的方法．例2　如图3－5－27所示，⊙O的直径AB长为6，弦AC长为2，∠ACB的平分线交⊙O于点D，求四边形ADBC的面积．图3－5－27【点悟】(1)本题把相等的圆周角转化为相等的弧，进而转化为相等的弦，然后利用勾股定理求出AD.
(2)圆周角的平分线是一个特别的条件． 如图3－5－28，在⊙O中，AB是直径，∠ACB的平分线交⊙O于点D，AD＝5 cm.求BD与⊙O半径的长．图3－5－28类型之二　利用圆周角定理及推论进行证明
例3　如图3－5－29所示，AB，CD是⊙O的直径，DF，BE是弦，且DF＝BE，求证：∠D＝∠B.图3－5－29 (1) (2)方法四：如图(3)所示，过O点作OM⊥FD于M，ON⊥BE于N.
∵DF＝BE，∴OM＝ON.∵OD＝OB，∴Rt△OMD≌Rt△ONB.∴∠D＝∠B. (3) (4)【点悟】 利用圆心角、弧、弦、弦心距之间的关系，从不同的角度加以证明，同时用直径所对的圆周角是直角的推论，添加常用辅助线构建三角形全等，使问题得到解决． 1.如图3－5－30所示，OA，OB，OC都是⊙O的半径，∠AOB＝2∠BOC.
求证：∠ACB＝2∠BAC.图3－5－302．如图3－5－31所示，在△ABC中，AC＝BC，以AC为直径作⊙O交AB于E，作△BCA的外角平分线CF交⊙O于F，连结EF.图3－5－31求证：EF＝BC.
证明：∵CA＝CB，∴∠B＝∠A，
又∵∠DCA＝∠A＋∠B，
CF平分∠DCA，
∴∠FCA＝∠A，∴CF∥AB.
∵∠FCA＝∠FEA，
∴∠FEA＝∠B，
∴BC∥EF，∴四边形CFEB为平行四边形，
∴EF＝BC.练 一 练