3.4圆心角定理的逆定理第2课时

课件32张PPT。第2课时 圆心角定理的逆定理【学习目标】
1．圆心角定理的逆定理的理解；
2．圆心角定理的逆定理的运用．
【学法指导】
1．通过理解圆的旋转不变性，理解圆心角定理的逆定理；
2．转化思想，把圆心角、弧、弦、弦心距利用圆心角定理的逆定理进行互相转化．填 一 填
圆心角定理的逆定理
在同圆或等圆中，如果______________、___________、__________、_____________中有一对量相等，那么它们所对应的其余各对量都相等．
说明：这个定理可以引导我们从多方面找出解决问题的方法，要解决弧相等的问题，可以从它们所对的弦、弦心距或所对的圆心角是否相等入手；要解决弦相等的问题，可以从它们所对的弧或所对的圆心角、弦心距是否相等入手．【知识管理】两个圆心角两条弧两条弦两个弦心距注意：在同圆或等圆中这一条件才能适用．
1．下列说法中正确的是 (　 　)
A．相等的弦所对的弧相等
B．相等的圆心角所对的弧相等
C．在同一个圆中相等的弧所对的弦相等
D．相等的弦所对的圆心角相等【对点自测】CA．1个　　　　　　 B．2个
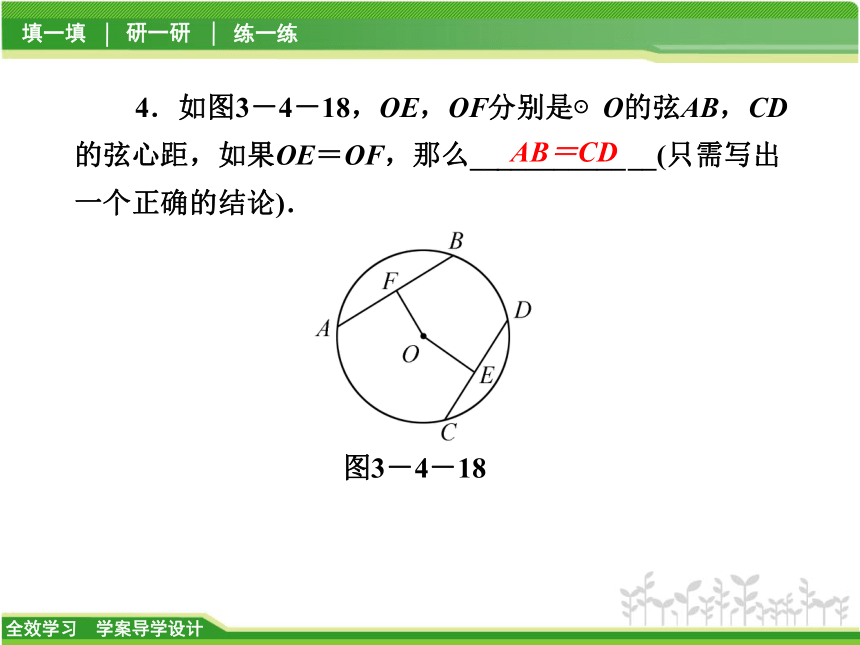
C．3个 D．4个D3．观察下列选项中的图及相应推理，其中正确的是 (　 　)ABBCD4．如图3－4－18，OE，OF分别是⊙O的弦AB，CD的弦心距，如果OE＝OF，那么_____________(只需写出一个正确的结论)．图3－4－18AB＝CD研 一 研类型之一　利用“弧、弦、圆心角、弦心距之间的关系”进行计算图3－4－19【点悟】 在同圆或等圆中，证明角相等，可以证明角所对的弧相等．图3－4－20图3－4－21类型之二　利用“弧、弦、圆心角、弦心距之间的关系”进行证明
例2　如图3－4－22所示，AB，AC，BC都是⊙O的弦，且∠CAB＝∠CBA，求证：∠COB＝∠COA.图3－4－22证明：∵∠CAB＝∠CBA(已知)，
∴AC＝BC(等角对等边)，
∴∠COB＝∠COA(在同一圆中，如果两条弦相等，那么它们所对的圆心角相等)．【点悟】 在同圆或等圆中，要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等，通常是转化成证明另外三组量中的某一组量相等． 1.如图3－4－23所示，已知⊙O中的弦AB＝CD.图3－4－232．已知：如图3－4－24，AB，CD是⊙O的两条弦，AB＝CD.
求证：∠OBA＝∠ODC.图3－4－24证明：过点O分别作OE⊥AB于点E，OF⊥CD于点F.
∵AB＝CD，∴OE＝OF.又∵BO＝DO，
∴Rt△BOE≌Rt△DOF(HL)，
∴∠OBA＝∠ODC.类型之三　弦、弧、圆心角、弦心距之间的关系与垂径定理的综合运用(1)试确定△ABC的形状；
(2)若AB＝a，求⊙O的半径．图3－4－25【点悟】 在解答圆的问题时，见到弧相等，常转化为它所对的圆心角相等，以及它们所对的弦相等． 1.已知⊙O是△ABC的外接圆，若AB＝AC＝5，BC＝6，则⊙O的半径为 (　 　)
A．4　　　　　　　 B．3.25
C．3.125 D．2.25C图3－4－26练 一 练