3.7正多边形

课件21张PPT。3.7 正多边形【学习目标】
1．掌握正多边形的概念及正多边形的内角计算；
2．理解正多边形的外接圆、圆内接正多边形的概念；
3．了解正多边形的尺规作图，能用正多边形设计图案．
?【学法指导】
1．正确地理解正多边形的含义，它要求从边和角的角度理解；
2．正多边形的计算归结为直角三角形的计算．填 一 填
1．正多边形的概念
定义：各边________、各_________也相等的多边形叫做正多边形；
特殊：正三角形、正方形、正五边形、正六边形．
2．正多边形的外接圆
正多边形的外接圆：经过一个正多边形的各个顶点的圆叫做这个_______________________；
圆内接正多边形：这个正多边形叫做_____________ _______．【知识管理】相等内角正多边形的外接圆圆内接正多边形注意：任何正多边形都有一个外接圆．
1．(知识点1)如果正多边形的一个外角等于45°，那么它的边数为 (　 　)
A．6　　　　　　 B．7
C．8 D．9【对点自测】A．正十二边形 B．正十边形
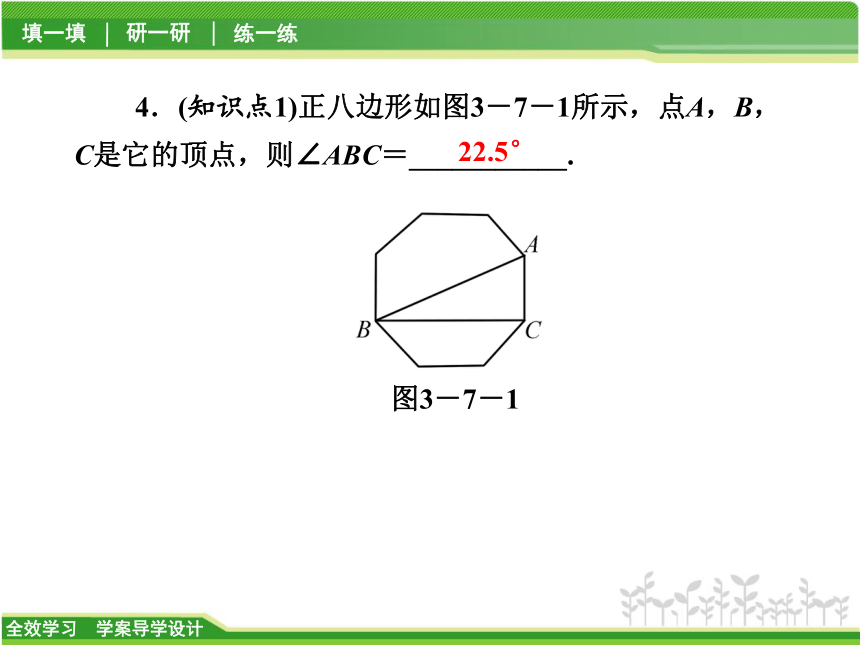
?C．正八边形 D．正六边形CB3．(知识点2)正三角形外接圆的半径为R，则三角形边长为 (　 　)A4．(知识点1)正八边形如图3－7－1所示，点A，B，C是它的顶点，则∠ABC＝___________.图3－7－122.5°研 一 研类型之一　正多边形的内角和解：设外角为x°，则内角为3x°，由题意得x＋3x＝180，
解得x＝45，360°÷45°＝8，
答：这个正多边形为八边形．【点悟】(1)多边形内角和等于(n－2)·180°；(2)多边形的外角和等于360°. 1.一个正多边形，它的每一个外角都是60°，则该正多边形是 (　 　)
A．正六边形　　　　　　　B．正七边形
C．正八边形 D．正九边形A(1)求正十边形的内角和；
(2)求n.类型之二　正多边形的计算
例2　正三角形边长为a，则其外接圆半径为 (　 　)A 1.圆的内接正四边形的边长与半径的比为 (　 　)C2．已知正六边形的外接圆半径为R，那么这个正六边形的边长为 (　 　)【解析】如图，正六边形的中心角∠AOB＝360°÷6＝60°，∵OA＝OB，∴△AOB是等边三角形，∵OA＝OB＝R，∴此正六边形的边长为R.A3．如图3－7－2，正六边形的螺帽的边长a＝17 mm，这个扳手的开口b最小应是多少？(结果精确到1 mm)图3－7－2类型之三　正多边形的证明
例3　如图3－7－3，已知正五边形ABCDE中，BF与CM相交于点P，CF＝DM.
(1)求证：△BCF≌△CDM.
(2)求∠BPM的度数．【解析】(1)由五边形ABCDE是正五边形，即可得BC＝CD，∠BCF＝∠CDM，然后利用SAS即可证得：△BCF≌△CDM.
图3－7－3(2)由五边形ABCDE是正五边形，即可求得∠BCF的度数，又由三角形内角和定理，求得∠CBF＋∠CFB的度数，然后由△BCF≌△CDM，可得∠MCD＝∠CBF，即可求得答案． 如图3－7－4，五边形ABCDE内接于⊙O，∠A＝∠B＝∠C＝∠D＝∠E.求证：五边形ABCDE是正五边形． 图3－7－4练 一 练