3.8扇形的面积第2课时

课件31张PPT。第2课时 扇形的面积【学习目标】
1．扇形的面积公式的理解与运用；
2．弓形面积的计算．
【学法指导】
1．在计算面积时，要注意观察和分析图形，把图形分解与组合，明确要计算的图形的面积；
2．掌握求图形的面积的常用方法，如割补法、几何变换法等；
3．思想方法：转化思想，把弓形的面积转化为扇形与三角形的面积的和(差).填 一 填
1．扇形的面积计算公式【知识管理】说明：扇形的半径为R，圆心角为n°，扇形的弧长为l，扇形面积为S.2．弓形的面积图3－8－12公式：如图3－8－12(1)所示，S弓形＝S扇形OAB－S△AOB.
如图3－8－12(2)所示，S弓形＝S扇形OAB＋S△AOB.
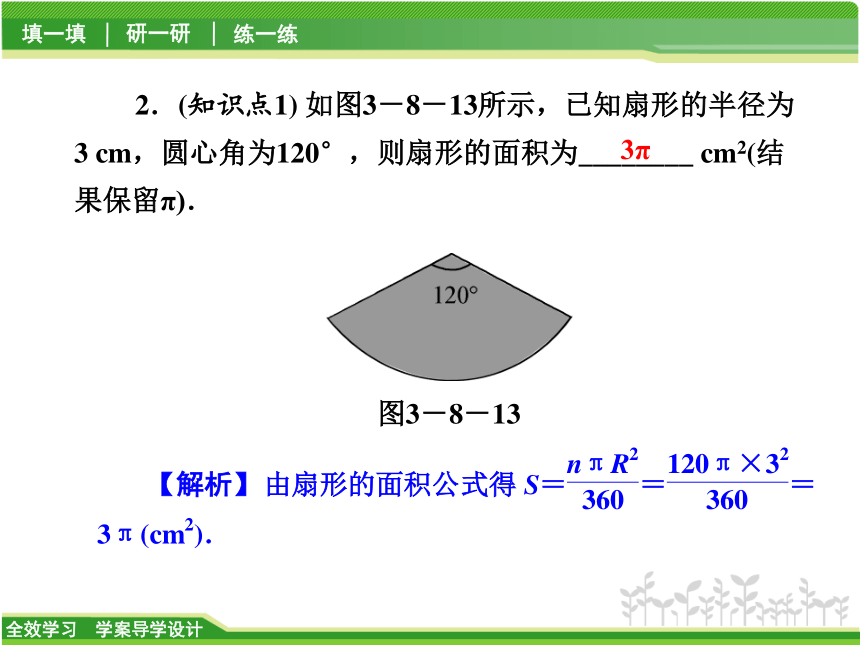
1．(知识点1)半径为R的圆中，圆心角为n°的扇形面积的计算公式是 (　 　)【对点自测】C2．(知识点1) 如图3－8－13所示，已知扇形的半径为3 cm，圆心角为120°，则扇形的面积为________ cm2(结果保留π)．图3－8－133π3．(知识点1) 扇形的弧长为4π，扇形的半径为3，则其面积为 (　 　)
A．12π B．6π
C．7π D．1.5πB4．(知识点2)在半径为2的圆中，长为2的弦与圆上劣弧所围成的弓形的面积是 (　 　)A研 一 研类型之一　计算扇形的面积
例1　如图3－8－14所示，圆心角为60°的扇形的半径为10 cm，求这个扇形的面积和周长．(π≈3.14)图3－8－14【点悟】 扇形周长＝弧长＋2×半径． 1.扇形的面积是12π，它的弧所对的圆心角为30°，则扇形的半径是 (　 　)
A．6　　　　　　　　B．24
C．12 D．10C2．扇形的弧长为20π cm，面积为240π cm2，那么扇形的半径是 (　 　)
A．6 cm B．12 cm
C．24 cm D．28 cmC3．已知一个扇形的弧长是20π cm，面积是240π cm2，则扇形的圆心角是_________度．150【点悟】 本题考查扇形的面积和弧长公式的综合运用．类型之二　计算弓形的面积(1)求⊙O的半径；
(2)求图中阴影部分的面积．图3－8－15【点悟】求阴影部分面积的问题，常用的方法有：直接运用公式法、和差法、割补法、等积代换法，把不规则的图形转化为规则图形． 1.如图3－8－16所示，AB为⊙O的直径，CD⊥AB于点E，交⊙O于点C，D，OF⊥AC于点F.图3－8－16(1)请写出三条与BC有关的正确结论；
(2)当∠D＝30°，BC＝1时，求图中阴影部分的面积．
解：(1)答案不唯一，只要合理均可，
例如：①BC＝BD；②OF∥BC；③∠BCD＝∠A；④BC2＝CE2＋BE2；⑤△ABC是直角三角形；⑥△BCD是等腰三角形．类型之三　求不规则图形(阴影部分)的面积
图3－8－17【解析】 通过割补，把S阴弓补到S白弓，把图中阴影部分面积转化为S△BCD，使问题得以解决．
解：∵OC⊥AB，∴∠AOC＝∠BOC＝90°.
∴S扇形OAC＝S扇形OBC.
∵AO＝BO，∴S△AOC＝S△OBC，
∴S扇形OAC－S△AOC＝S扇形OBC－S△OBC，
∴阴影部分的面积等于S△BCD.
∵OB＝OC，∴∠OBC＝∠OCB＝45°，
∵∠ABD＝105°，
∴∠CBD＝∠ABD－∠OBC＝105°－45°＝60°.
∵AB是直径，∴∠ACB＝∠BCD＝90°.【点悟】 采用割补法，必须是割去部分面积等于补上部分的面积，思考时应努力从图形中找出面积相等的部分．图3－8－18C图3－8－19图3－8－20【点悟】 该题利用同底等高的两个三角形面积相等把△PCD的面积转化为△CDO的面积．把阴影部分的面积转化为扇形面积体现了转化思想．练 一 练