4.4两个三角形相似的判定(3)

(共25张PPT)
第3课时 两个三角形相似的判定(3)
【学习目标】
理解并掌握“三边对应成比例的两个三角形相似”的判
定方法．
【学法指导】
类比全等三角形判定方法SSS理解“三边对应成比例的两个三角形相似”的判定方法．
填 一 填
三角形相似的判定方法
定理3：三边对应成比例的两个三角形相似．
【知识管理】
注意：三边对应成比例的两个三角形相似，三边对应是有序的，即：大对大，小对小，中对中．
1．下列判断中，正确的个数有 (　 　)
①全等三角形是相似三角形
②顶角相等的两个等腰三角形相似
③所有的等边三角形都相似
④所有的直角三角形都相似
A．1个　　　　　　 B．2个
C．3个 D．4个
【对点自测】
C
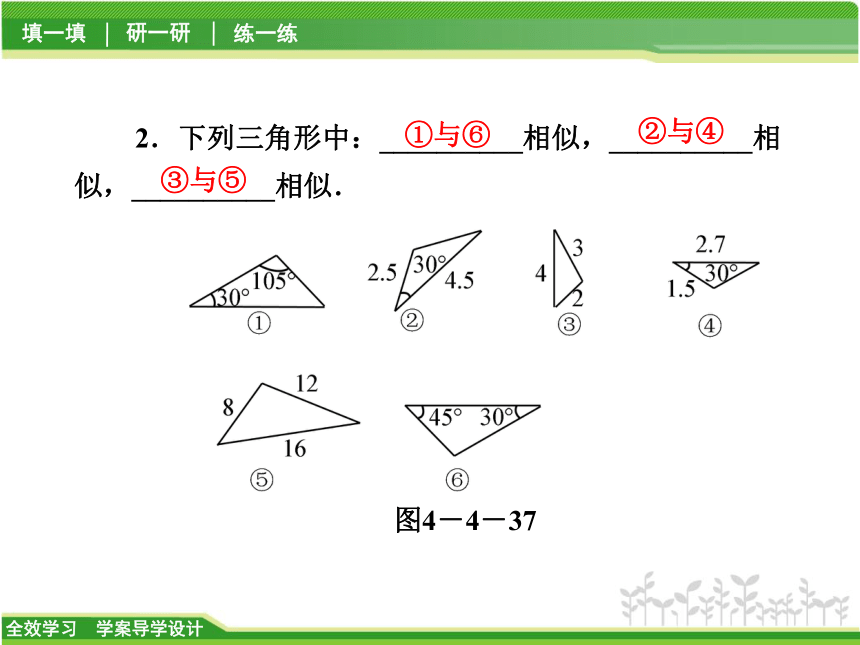
2．下列三角形中：__________相似，__________相似，__________相似．
图4－4－37
①与⑥
②与④
③与⑤
3．如图4－4－38，△ABC三边长分别为AB＝3 cm，BC＝3.5 cm，CA＝2.5 cm；△DEF三边长分别为DE＝3.6 cm，EF＝4.2 cm，FD＝3 cm.△ABC与△DEF是否相似？为什么？
图4－4－38
4．下列四组三角形中，相似的一组是 (　 　)
A．Rt△ABC中，直角边BC＝6，斜边AB＝10；Rt△A′B′C′中，两条直角边A′C′＝16，B′C′＝12
B．△ABC中，∠A＝42°，∠B＝118°；△A′B′C′中，∠A′＝118°，∠B′＝15°
C．△ABC中，AB＝8，AC＝4，∠A＝105°；△A′B′C′中，A′B′＝16，B′C′＝4，∠A′＝100°
D．△ABC中，AB＝8，BC＝20，CA＝35；△A′B′C′中，A′B′＝36，B′C′＝40，C′A′＝75
A
研 一 研
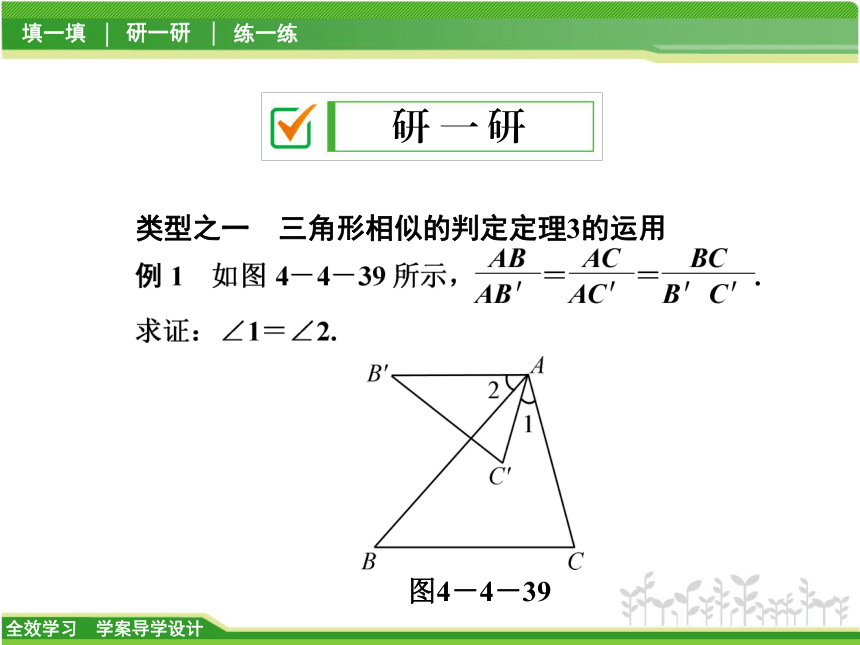
类型之一　三角形相似的判定定理3的运用
图4－4－39
【解析】 由三边对应成比例，得到ABC∽△AB′C′，从而对应角相等．
【点悟】 要证两角相等，找出与它们有关的两个三角形相似是一种重要的解题方法．
1.已知：在△ABC中，AB＝4，BC＝5，CA＝6.
(1)如果DE＝10，那么当EF＝________，FD＝_____时，△DEF∽△ABC；
(2)如果DE＝10，那么当EF＝______，FD＝_____时，△FDE∽△ABC.
12.5
15
12
8
图4－4－40
图4－4－41
类型之二　格点三角形的相似的判定
例2　如图4－4－42所示，方格纸中每个小正方形的边长为1，△ABC和△DEF的顶点都在方格纸的格点上．
图4－4－42
(1)判断△ABC和△DEF是否相似，并说明理由；
(2)P1，P2，P3，P4，P5，D，F是△DEF边上的7个格点，请在这7个格点中选取3个点作为三角形的顶点，使构
成的三角形与△ABC相似(要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由)．
(2)答案不唯一，下面6个三角形中的任意2个均可．
△P2P5D，△P4P5F，△P2P4D，
△P4P5D，△P2P4P5，△P1FD.
【点悟】 利用网格构成直角三角形，根据勾股定理计算所在三角形的边，从而计算对应边的比，运用两边对应成比例，且夹角相等，或三边对应成比例说明两个三角形相似，这是代数与几何的融合，也是几何知识的相互沟通，体现了数形结合思想．
1.如图4－4－43，将方格纸分成6个三角形，在②，③，④，⑤，⑥5个三角形中，与三角形①相似的三角形有______.
③
图4－4－43
2．如图4－4－44，在正方形网格上，每个小正方形的边长为a，那么△ABC与△A1B1C1是否相似？为什么？
图4－4－44
3．如图4－4－45，在矩形ABEF中，四边形ABCH、四边形CDGH和四边形DEFG都是正方形，图中的△ACD与△ECA相似吗？为什么？
图4－4－45
练 一 练