浙教版八年级上册 5.1 常量与变量 课件(共19张PPT)
文档属性
| 名称 | 浙教版八年级上册 5.1 常量与变量 课件(共19张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 06:43:15 | ||
图片预览







文档简介
(共19张PPT)
情境
引入
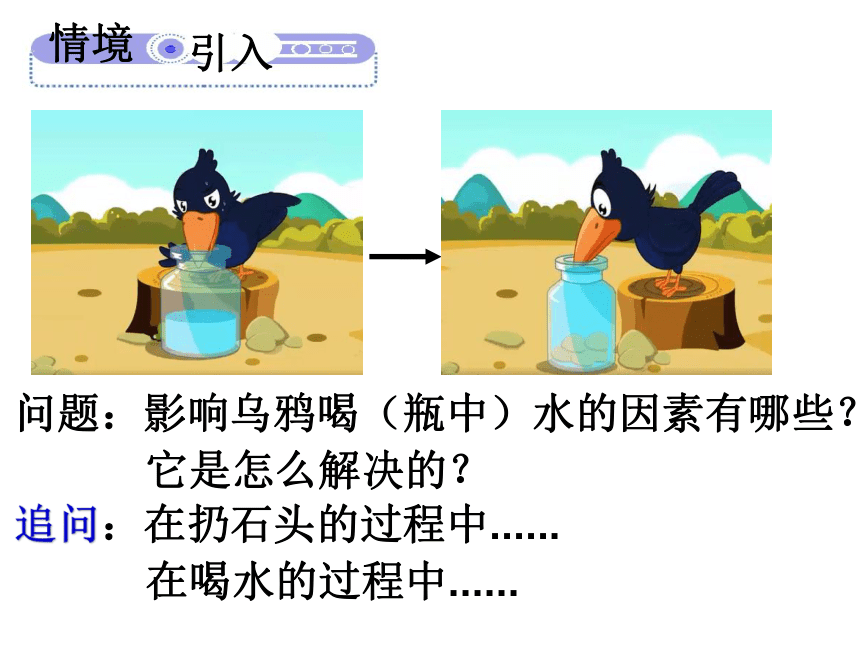
问题:影响乌鸦喝(瓶中)水的因素有哪些?
它是怎么解决的?
追问:在扔石头的过程中......
在喝水的过程中......
从数学的角度来分析现实世界的各种现象时,会遇到各种各样的量.例如,
在某一个过程中,有些量固定不变,有些量不断改变,并且一个量会随着另一个量的变化而变化.
物体运动中的速度、时间和距离;
圆的半径、周长和圆周率;
购买商品的数量、单价和总价;
工程问题中的工作效率、工作时间、工作总量;
某城市一天中各时刻变化着的气温;
某段河道一天中时刻变化着的水位;
……
1. 石头丢入水面形成了涟漪,圆形水波慢慢扩大,在这一过程中,当 r取一些不同的值时, 圆的面积 S 的值:
问题: 在圆形水波慢慢扩大的过程中,存在着
哪些量?
问题
探究
追问1:填写表格并思考:s的值随着r的值变化
而变化吗?
…
…
3
2
1.5
追问2:哪些量的值发生变化,哪些量的值不变?
2. 已知绘本《乌鸦喝水》的售价为8元/本, 设三次购买绘本的数量分别为5本,6本,7本,三次购买绘本的总价各为多少元?
②在计算总价的过程中,哪些量发生了变化?
哪些量不变?
①设购买绘本数量为x本,总价为y元,y随x的值
变化而变化吗?
3. 用10米长的绳子围一个长方形,当长方形的一边 x分别为3米,3.5米,4米,4.5米时,它邻边为 y 分别为多少?
②在这一变化过程中,哪些量发生了变化?
哪些量不变?
①思考:y的值随x的值变化而变化吗?
在一个变化过程中,数值发生变化的量称为变量,数值始终不变的量称为常量.
初识
概念
归纳:在不同事物的变化过程中...
5.1 常量和变量
固定速度 v 千米/时,
若设行驶的时间为 t 小时,路程为 s千米,则路程 s与时间 t
的关系式为_________,其中常量是__________,变量是_____.
常量不一定是具体的数,也可以用字母表示.
理解
概念
1. 某货车行驶的平均速度为
80千米/时
80千米/时,
若设货车行驶的平均速度为v千米/时,行驶完全程所需的时间
为 t 小时,则时间 t =_______,其中常量是___________,
变量是_______.
变式:三门与宁波相距约150千米,
150千米
在一个过程中,常量与变量相对地存在.
过程 常量 变量
在v一定的过程中
v
在s一定的过程中
s
在t一定的过程中
t
1. 货车以80千米/时的平均速度行驶
2. 三门与宁波相距约150千米,
货车从三门向宁波行驶
3. 货车计划下午2点从三门出发,
4点30到宁波
判断常量、变量的步骤
①明确一个变化过程
③再判断常量和变量
数学问题
数学眼光
实际问题
一、
二、
②寻找这些量之间的
变化规律或数量关系
2.如图是某日宁波24小时气温变化图,其中图上的点横坐标x表示时间,纵坐标y表示气温.
(1)指出气温变化图中的变量.
式
表
图
3.一长方形的面积为S,一边长为x,另一边为y.
问题:s的值随着x值的变化而变化吗?
追问:哪些是变量,哪些是常量?
一家快递公司的收费标准如图,用 m表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
m(千克) 3 6 10 11 12.5 13
p(元)
6
6
6
7
9
9
(1)填写下表
概念
应用
概念
应用
(2)在投寄快递邮件的事项中,m、p、n是常量还是变量?
一家快递公司的收费标准如图,用 m 表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
追问:当11<m≤12,p是否为常量?当11≤m≤12呢?
(3)当0<m≤10,邮寄n件快递的费用为w,这时哪些量是常量 , 哪些是变量?
概念
应用
一家快递公司的收费标准如图,用 m 表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
回顾
小结
1.我们学习了什么内容?
2.我们是怎样学习的?
3.研究了常量和变量后,
后续研究什么?
现实世界
各种量及数量关系
前提: 在一个变化过程中
判断依据:数值是否变化
定义
数量
关系
提出问题
抽象
式子
表格
图
定性
定量
你到哪里去,亲爱的朋友?
你从哪里来
从一个故事中走来,从一个抽象的过程
与数学内部发展中走来......
从一个变化的过程中走来,带来两个“变化”:从“定性”分析,走向“定量”分析,从“常量数学”走向“变量数学”。
课后作业:
必做题:作业本(1)P23-24
时间是个常量,每年365天,谁都不会少。对勤奋者来说,时间却是个变量,在有限的时间单位里实现更多愿望,正是生命意义之所在。
——选自《人民日报》2017年1月5日版
情境
引入
问题:影响乌鸦喝(瓶中)水的因素有哪些?
它是怎么解决的?
追问:在扔石头的过程中......
在喝水的过程中......
从数学的角度来分析现实世界的各种现象时,会遇到各种各样的量.例如,
在某一个过程中,有些量固定不变,有些量不断改变,并且一个量会随着另一个量的变化而变化.
物体运动中的速度、时间和距离;
圆的半径、周长和圆周率;
购买商品的数量、单价和总价;
工程问题中的工作效率、工作时间、工作总量;
某城市一天中各时刻变化着的气温;
某段河道一天中时刻变化着的水位;
……
1. 石头丢入水面形成了涟漪,圆形水波慢慢扩大,在这一过程中,当 r取一些不同的值时, 圆的面积 S 的值:
问题: 在圆形水波慢慢扩大的过程中,存在着
哪些量?
问题
探究
追问1:填写表格并思考:s的值随着r的值变化
而变化吗?
…
…
3
2
1.5
追问2:哪些量的值发生变化,哪些量的值不变?
2. 已知绘本《乌鸦喝水》的售价为8元/本, 设三次购买绘本的数量分别为5本,6本,7本,三次购买绘本的总价各为多少元?
②在计算总价的过程中,哪些量发生了变化?
哪些量不变?
①设购买绘本数量为x本,总价为y元,y随x的值
变化而变化吗?
3. 用10米长的绳子围一个长方形,当长方形的一边 x分别为3米,3.5米,4米,4.5米时,它邻边为 y 分别为多少?
②在这一变化过程中,哪些量发生了变化?
哪些量不变?
①思考:y的值随x的值变化而变化吗?
在一个变化过程中,数值发生变化的量称为变量,数值始终不变的量称为常量.
初识
概念
归纳:在不同事物的变化过程中...
5.1 常量和变量
固定速度 v 千米/时,
若设行驶的时间为 t 小时,路程为 s千米,则路程 s与时间 t
的关系式为_________,其中常量是__________,变量是_____.
常量不一定是具体的数,也可以用字母表示.
理解
概念
1. 某货车行驶的平均速度为
80千米/时
80千米/时,
若设货车行驶的平均速度为v千米/时,行驶完全程所需的时间
为 t 小时,则时间 t =_______,其中常量是___________,
变量是_______.
变式:三门与宁波相距约150千米,
150千米
在一个过程中,常量与变量相对地存在.
过程 常量 变量
在v一定的过程中
v
在s一定的过程中
s
在t一定的过程中
t
1. 货车以80千米/时的平均速度行驶
2. 三门与宁波相距约150千米,
货车从三门向宁波行驶
3. 货车计划下午2点从三门出发,
4点30到宁波
判断常量、变量的步骤
①明确一个变化过程
③再判断常量和变量
数学问题
数学眼光
实际问题
一、
二、
②寻找这些量之间的
变化规律或数量关系
2.如图是某日宁波24小时气温变化图,其中图上的点横坐标x表示时间,纵坐标y表示气温.
(1)指出气温变化图中的变量.
式
表
图
3.一长方形的面积为S,一边长为x,另一边为y.
问题:s的值随着x值的变化而变化吗?
追问:哪些是变量,哪些是常量?
一家快递公司的收费标准如图,用 m表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
m(千克) 3 6 10 11 12.5 13
p(元)
6
6
6
7
9
9
(1)填写下表
概念
应用
概念
应用
(2)在投寄快递邮件的事项中,m、p、n是常量还是变量?
一家快递公司的收费标准如图,用 m 表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
追问:当11<m≤12,p是否为常量?当11≤m≤12呢?
(3)当0<m≤10,邮寄n件快递的费用为w,这时哪些量是常量 , 哪些是变量?
概念
应用
一家快递公司的收费标准如图,用 m 表示邮件的质量,p 表示每件快递费,n表示快递邮件的件数.
回顾
小结
1.我们学习了什么内容?
2.我们是怎样学习的?
3.研究了常量和变量后,
后续研究什么?
现实世界
各种量及数量关系
前提: 在一个变化过程中
判断依据:数值是否变化
定义
数量
关系
提出问题
抽象
式子
表格
图
定性
定量
你到哪里去,亲爱的朋友?
你从哪里来
从一个故事中走来,从一个抽象的过程
与数学内部发展中走来......
从一个变化的过程中走来,带来两个“变化”:从“定性”分析,走向“定量”分析,从“常量数学”走向“变量数学”。
课后作业:
必做题:作业本(1)P23-24
时间是个常量,每年365天,谁都不会少。对勤奋者来说,时间却是个变量,在有限的时间单位里实现更多愿望,正是生命意义之所在。
——选自《人民日报》2017年1月5日版
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
