第4章 相似三角形›章末复习课
文档属性
| 名称 | 第4章 相似三角形›章末复习课 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-18 12:38:51 | ||
图片预览










文档简介
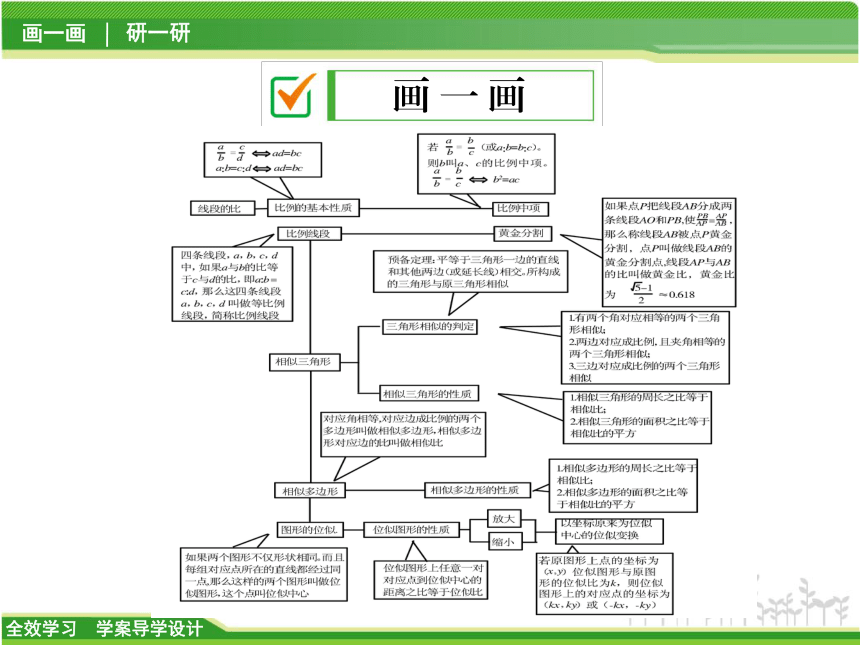
课件41张PPT。第4章 相似三角形章末复习课画 一 画研 一 研类型之一 比例线段C 1.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为
( )
A.4.8米 B.6.4米
C.9.6米 D.10米C24类型之二 平行线分线段成比例定理
在运用平行线分线段成比例定理时要注意弄清三条平行线截两条直线,所得哪条线段与哪条线段是对应线段,同时要根据需要写出正确的比例式.
例2 已知:如图4-1,l1∥l2∥l3,AB=3,DE=2,EF=4,求BC.图4-1图4-2类型之三 相似三角形的判定
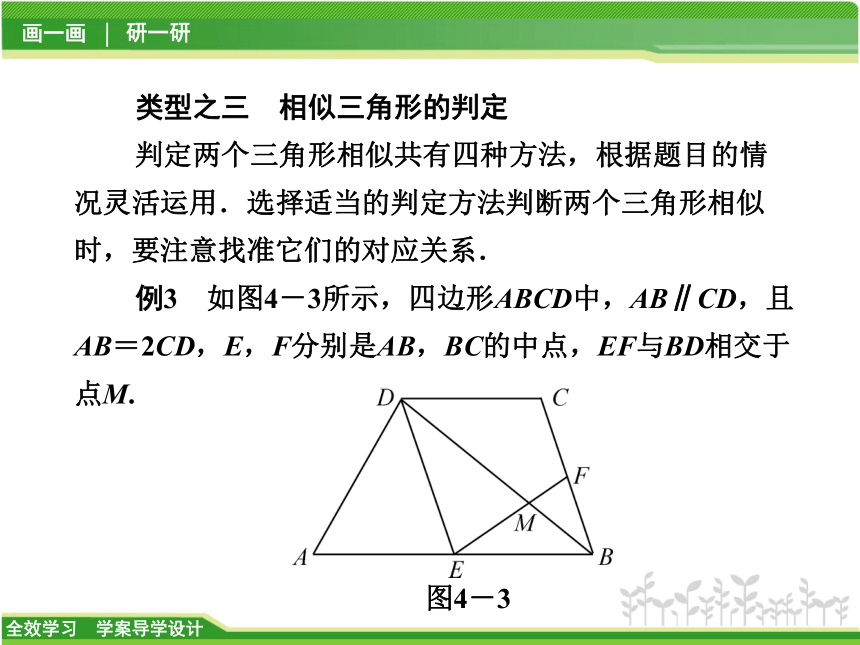
判定两个三角形相似共有四种方法,根据题目的情况灵活运用.选择适当的判定方法判断两个三角形相似时,要注意找准它们的对应关系.
例3 如图4-3所示,四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
图4-3(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
【解析】 ∵AB=2CD,E是AB的中点,可先证明四边形BCDE是平行四边形,然后就证得△EDM∽△FBM.
解:(1)∵E是AB的中点,∴AB=2EB.∵AB=2CD,∴CD=EB.
又∵AB∥CD,∴四边形CBED是平行四边形,
∴CB∥DE,∴∠DEM=∠BFM,∠EDM=∠FBM,
∴△EDM∽△FBM.【点悟】 本题按常规方法即可求解. 1.如图4-4所示,AB∥CD,AE∥FD,AE,FD分别与BC交于点G,H,则图中共有相似三角形
( )C图4-4A.4对 B.5对
C.6对 D.7对
【解析】 △BFH∽△BAG,△BFH∽△CDH,
△BFH∽△CEG,△BAG∽△CEG,△ABG∽△DCH,△CEG∽△CDH,故选C.
【点悟】 按一定的顺序来寻找相似三角形.2.如图4-5所示,已知∠1=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立.
(1)写出这个条件(至少写出3个);
(2)对其中的一个予以证明.图4-5【点悟】 对已知条件和结论先进行正确地分析,然后再增加条件.3.如图4-6所示,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.我们知道,结论“Rt△AEP∽Rt△DPC”成立.
(1)当CPD=30°时,求AE的长;
(2)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.图4-6类型之四 相似三角形的性质
对应角相等,对应边成比例是相似三角形的本质属性.相似三角形的对应高之比,对应中线之比,对应角平分线之比,周长之比都等于相似比.相似三角形面积之比等于相似比的平方.解题时常需灵活运用这些性质.例4 如图4-7,?ABCD中,E是AB延长线上一点,DE交BC于点F,已知BE∶AB=2∶3,S△BEF=4,求S△CDF.
图4-7 1.两个相似三角形的面积比是3∶4,则这两个三角形的相似比是 ( )
A.9∶16 B.3∶4D2.如图4-8所示,若Rt△ABC中,∠ACB=90°,CD为斜边上的高,AC=m,AB=n,则△BCD的面积与△ACD的面积比的值是 ( )图4-8C3.如图4-9所示,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有_________.图4-9①②④类型之五 相似三角形的应用
会设计利用相似三角形解决问题的方案;会构造(画)与实物相似的三角形;会运用相似三角形的判定、性质性行计算.
例5 一块直角三角形木板的直角边AB=1.5 m,BC=2 m,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图4-10(1)所示,乙设计方案如图4-10(2)所示.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果可保留分数)图4-10?
【解析】 本题是相似三角形应用的经典题,对于甲、乙设计方案谁优?谁劣?根据相似三角形的性质通过计算进行比较说明.【点悟】 比较某几个设计方案的好坏,一般的方法就是进行计算来比较好坏,运用数据来说明问题,数据是最具有说服力的证据. 检查视力时,规定人与视力表之间的距离应为5米.如图4-11(1),现因房间两面墙的距离为3米,因此使用平面镜来解决房间小的问题.若使墙面镜子能呈现完整的视力表,如图4-11(2),由平面镜成像原理,作出了光路图,其中视力表A,B的上下边沿A,B发出的光线经平面镜MM′的上下边沿反射后射入人眼C处.如果视力表的全长为0.8米,请计算出镜长至少为多少米?图4-11解: 作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,∴CE⊥A′B′,类型之六 位似图形的作法及位似变换
位似图形上任意一对对应点到位似中心的距离之比等于位似比,在坐标系中若原图形上某点的坐标为(x,y),位似图形与原图形的位似比为k,则位似图形上的对应点的坐标为(kx,ky)或(-kx,-ky).例6 如图4-12所示,在所给网格图(每小格均为边长是1的正方形)中完成下列各题.
图4-12(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M,N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少?(注:只要写出对应边的比即可)
(3)求图形A2B2C2D2的面积.
【解析】(1)根据成轴对称图形的对应点的连结线段的垂直平分线就是对称轴确定MN的位置;
(2)由对应点D和D2可知图形ABCD与图形A2B2C2D2的对应边的比是1∶2;
(3)B2D2⊥A2C2,S四边形A2B2C2D2=S△A2B2D2+S△B2C2D2.解:(1)如图所示,画出对称轴MN; 在下列方格纸中,
(1)画出△ABC关于直线l对称的图形△A1B1C1;
(2)以O为位似中心,将△ABC放大到原来的2倍得△A2B2C2.(保留作图痕迹)
图4-13解:(1)如图所示,△A1B1C1即为所求;
图4-13
(2)如图所示,△A2B2C2即为所求.
类型之七 圆中图形的相似
证明圆中图形的相似问题,常用到圆心角、弧、弦、弦心距之间的相互关系的定理、圆周角定理及逆定理进行角度转换.
例7 如图4-14,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽ △AEB;
(2)若AD=1,DE=3, 求BD的长.图4-14 如图4-15,△ABC的两个顶点B,C在圆上,顶点A在圆外,AB,AC分别交圆于E,D两点,连结EC,BD.图4-15(1)求证:△ABD∽△ACE;
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的形状.
∴∠EBD=∠ECD,
又∵∠A=∠A,
∴△ABD∽△ACE;
(2)因为S△BEC=S△BCD,
S△ACE=S△ABC-S△BEC,S△ABD=S△ABC-S△BCD,
所以S△ACE=S△ABD,
又由(1)知△ABD∽△ACE,
所以对应边之比等于1,
所以AB=AC,即△ABC为等腰三角形.
( )
A.4.8米 B.6.4米
C.9.6米 D.10米C24类型之二 平行线分线段成比例定理
在运用平行线分线段成比例定理时要注意弄清三条平行线截两条直线,所得哪条线段与哪条线段是对应线段,同时要根据需要写出正确的比例式.
例2 已知:如图4-1,l1∥l2∥l3,AB=3,DE=2,EF=4,求BC.图4-1图4-2类型之三 相似三角形的判定
判定两个三角形相似共有四种方法,根据题目的情况灵活运用.选择适当的判定方法判断两个三角形相似时,要注意找准它们的对应关系.
例3 如图4-3所示,四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
图4-3(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
【解析】 ∵AB=2CD,E是AB的中点,可先证明四边形BCDE是平行四边形,然后就证得△EDM∽△FBM.
解:(1)∵E是AB的中点,∴AB=2EB.∵AB=2CD,∴CD=EB.
又∵AB∥CD,∴四边形CBED是平行四边形,
∴CB∥DE,∴∠DEM=∠BFM,∠EDM=∠FBM,
∴△EDM∽△FBM.【点悟】 本题按常规方法即可求解. 1.如图4-4所示,AB∥CD,AE∥FD,AE,FD分别与BC交于点G,H,则图中共有相似三角形
( )C图4-4A.4对 B.5对
C.6对 D.7对
【解析】 △BFH∽△BAG,△BFH∽△CDH,
△BFH∽△CEG,△BAG∽△CEG,△ABG∽△DCH,△CEG∽△CDH,故选C.
【点悟】 按一定的顺序来寻找相似三角形.2.如图4-5所示,已知∠1=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立.
(1)写出这个条件(至少写出3个);
(2)对其中的一个予以证明.图4-5【点悟】 对已知条件和结论先进行正确地分析,然后再增加条件.3.如图4-6所示,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.我们知道,结论“Rt△AEP∽Rt△DPC”成立.
(1)当CPD=30°时,求AE的长;
(2)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.图4-6类型之四 相似三角形的性质
对应角相等,对应边成比例是相似三角形的本质属性.相似三角形的对应高之比,对应中线之比,对应角平分线之比,周长之比都等于相似比.相似三角形面积之比等于相似比的平方.解题时常需灵活运用这些性质.例4 如图4-7,?ABCD中,E是AB延长线上一点,DE交BC于点F,已知BE∶AB=2∶3,S△BEF=4,求S△CDF.
图4-7 1.两个相似三角形的面积比是3∶4,则这两个三角形的相似比是 ( )
A.9∶16 B.3∶4D2.如图4-8所示,若Rt△ABC中,∠ACB=90°,CD为斜边上的高,AC=m,AB=n,则△BCD的面积与△ACD的面积比的值是 ( )图4-8C3.如图4-9所示,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有_________.图4-9①②④类型之五 相似三角形的应用
会设计利用相似三角形解决问题的方案;会构造(画)与实物相似的三角形;会运用相似三角形的判定、性质性行计算.
例5 一块直角三角形木板的直角边AB=1.5 m,BC=2 m,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图4-10(1)所示,乙设计方案如图4-10(2)所示.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果可保留分数)图4-10?
【解析】 本题是相似三角形应用的经典题,对于甲、乙设计方案谁优?谁劣?根据相似三角形的性质通过计算进行比较说明.【点悟】 比较某几个设计方案的好坏,一般的方法就是进行计算来比较好坏,运用数据来说明问题,数据是最具有说服力的证据. 检查视力时,规定人与视力表之间的距离应为5米.如图4-11(1),现因房间两面墙的距离为3米,因此使用平面镜来解决房间小的问题.若使墙面镜子能呈现完整的视力表,如图4-11(2),由平面镜成像原理,作出了光路图,其中视力表A,B的上下边沿A,B发出的光线经平面镜MM′的上下边沿反射后射入人眼C处.如果视力表的全长为0.8米,请计算出镜长至少为多少米?图4-11解: 作CD⊥MM′,垂足为D,并延长交A′B′于E,
∵AB∥MM′∥A′B′,∴CE⊥A′B′,类型之六 位似图形的作法及位似变换
位似图形上任意一对对应点到位似中心的距离之比等于位似比,在坐标系中若原图形上某点的坐标为(x,y),位似图形与原图形的位似比为k,则位似图形上的对应点的坐标为(kx,ky)或(-kx,-ky).例6 如图4-12所示,在所给网格图(每小格均为边长是1的正方形)中完成下列各题.
图4-12(1)图形ABCD与图形A1B1C1D1关于直线MN成轴对称,请在图中画出对称轴并标注上相应字母M,N;
(2)以图中O点为位似中心,将图形ABCD放大,得到放大后的图形A2B2C2D2,则图形ABCD与图形A2B2C2D2的对应边的比是多少?(注:只要写出对应边的比即可)
(3)求图形A2B2C2D2的面积.
【解析】(1)根据成轴对称图形的对应点的连结线段的垂直平分线就是对称轴确定MN的位置;
(2)由对应点D和D2可知图形ABCD与图形A2B2C2D2的对应边的比是1∶2;
(3)B2D2⊥A2C2,S四边形A2B2C2D2=S△A2B2D2+S△B2C2D2.解:(1)如图所示,画出对称轴MN; 在下列方格纸中,
(1)画出△ABC关于直线l对称的图形△A1B1C1;
(2)以O为位似中心,将△ABC放大到原来的2倍得△A2B2C2.(保留作图痕迹)
图4-13解:(1)如图所示,△A1B1C1即为所求;
图4-13
(2)如图所示,△A2B2C2即为所求.
类型之七 圆中图形的相似
证明圆中图形的相似问题,常用到圆心角、弧、弦、弦心距之间的相互关系的定理、圆周角定理及逆定理进行角度转换.
例7 如图4-14,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽ △AEB;
(2)若AD=1,DE=3, 求BD的长.图4-14 如图4-15,△ABC的两个顶点B,C在圆上,顶点A在圆外,AB,AC分别交圆于E,D两点,连结EC,BD.图4-15(1)求证:△ABD∽△ACE;
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的形状.
∴∠EBD=∠ECD,
又∵∠A=∠A,
∴△ABD∽△ACE;
(2)因为S△BEC=S△BCD,
S△ACE=S△ABC-S△BEC,S△ABD=S△ABC-S△BCD,
所以S△ACE=S△ABD,
又由(1)知△ABD∽△ACE,
所以对应边之比等于1,
所以AB=AC,即△ABC为等腰三角形.
同课章节目录
