1.1 锐角三角函数的概念第1课时
图片预览






文档简介
课件27张PPT。第1章 解直角三角形1.1 锐角三角函数第1课时 锐角三角函数的概念【学习目标】
1.理解锐角三角函数的概念,并能将三角函数表示为 两条线段的比;
2.了解直角三角形中的两个锐角三角函数值之间的关 系;
3.了解直角三角形中的边与三角函数值的关系.
【学法指导】
1. 从定义出发,加强对三角函数的理解;
2.在求三角函数值的过程中,体会数形结合的思想方 法.填 一 填
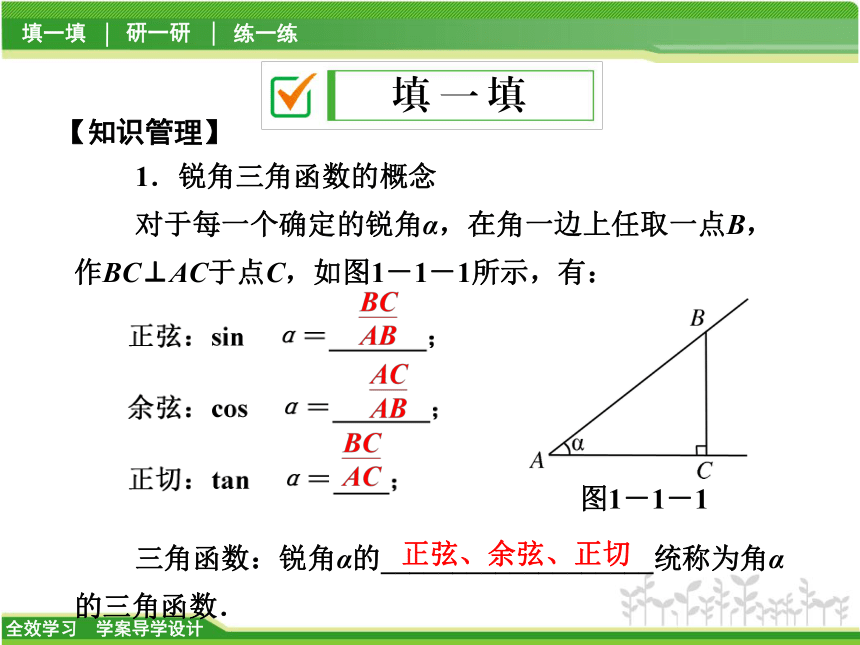
1.锐角三角函数的概念
对于每一个确定的锐角α,在角一边上任取一点B,作BC⊥AC于点C,如图1-1-1所示,有:
三角函数:锐角α的___________________统称为角α的三角函数.【知识管理】图1-1-1正弦、余弦、正切2.直角三角形中的边角关系
范围:______01013.余角间的函数关系
公式:当∠A+∠B=90°时,sin A=_________;
tan A·tan B=______.cos B1
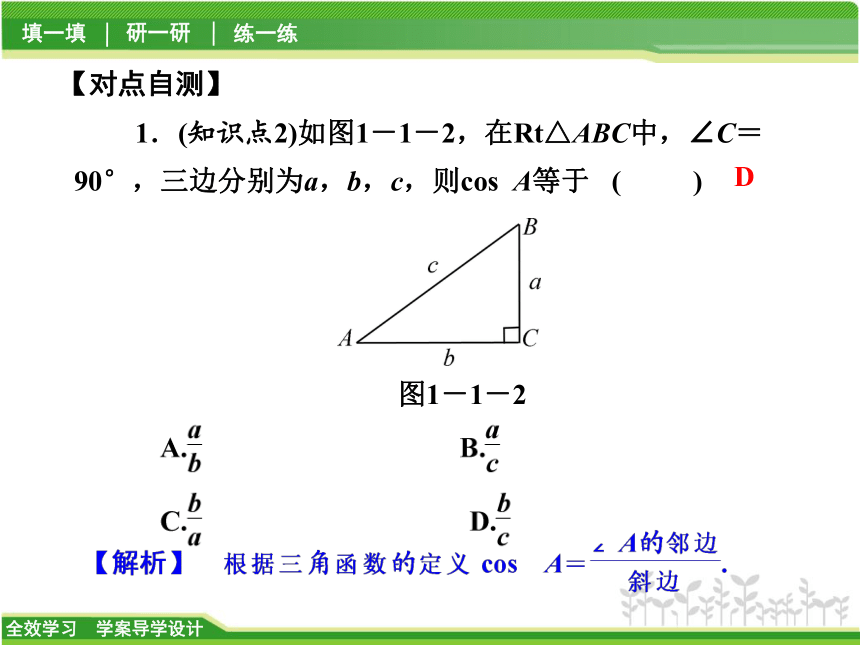
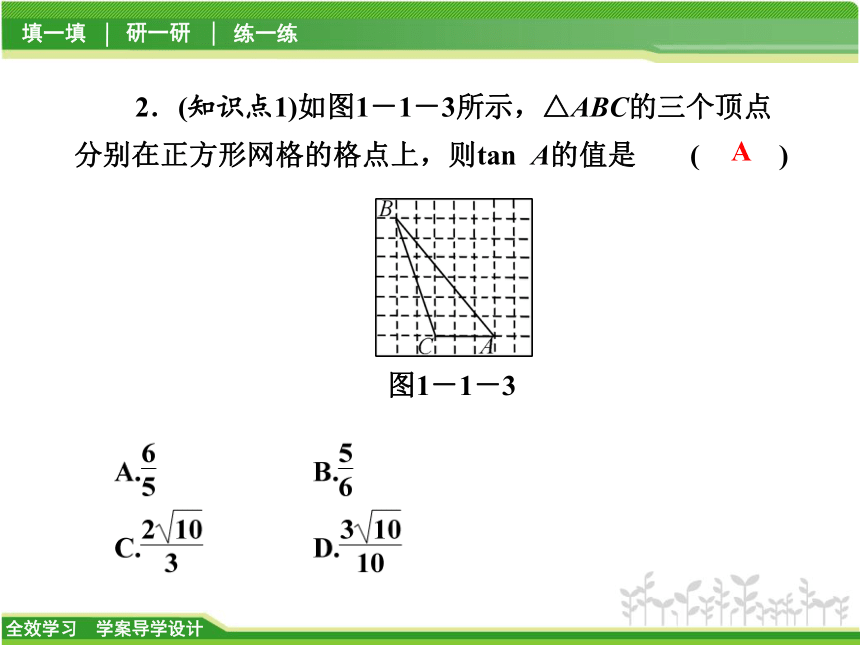
1.(知识点2)如图1-1-2,在Rt△ABC中,∠C=90°,三边分别为a,b,c,则cos A等于 ( )【对点自测】D图1-1-22.(知识点1)如图1-1-3所示,△ABC的三个顶点分别在正方形网格的格点上,则tan A的值是 ( )图1-1-3A2图1-1-46研 一 研类型之一 求直角三角形中锐角的三角函数值
例1 如图1-1-5所示,Rt△ABC中,∠C=90°,AC=8,BC=6,求sin A,cos A,tan B的值.图1-1-5【点悟】 运用三角函数的定义解题是在直角三角形中进行的,因此通常先运用勾股定理求未知边,从而求三角函数值. 1.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cos A的值是 ( )B2.在Rt△ABC中,∠C=90°,AC=5,AB=13,
则tan A+tan B=________.
3.如图1-1-6所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若b=2a,则tan
A=____.
图1-1-6类型之二 已知直角三角形中的一锐角三角函数值,求这一锐角的其他三角函数值
(1)求出∠A,∠B的其他三角函数值;
(2)比较结果,你有什么发现?
图1-1-7【解析】 本题不能直接求出边长,但在Rt△ABC中给出了cos A的值,而要求的其他三角函数值是一个比值,故设AC=3k,AB=4k,可由勾股定理求出BC,从而达到目的.【点悟】(1)求一个锐角的三角函数值,关键是理解其意义,不需要求直角三角形各边之长,只知道它们的比值,同样可求出其他三角函数值.(2)知道比值往往设比值,即用k表示各边之长,这种转化的思想要掌握. 1.如图1-1-8所示,图(1)是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图(2),那么在Rt△ABC中,sin B的值是
( )B图1-1-8A类型之三 求非直角三角形中的三角函数值
例3 如图1-1-9所示,在△ABC中,AB=15,AC=13,S△ABC=84,求sin A的值.
【解析】 求sin A的值,由正弦定义可知,必须构造直角三角形,已知三角形面积,故作CD⊥AB于D,可解决问题.图1-1-9【点悟】 作三角形一边上的高,构造直角三角形是利用三角函数值解非直角三角形的常用方法,此题考查三角函数与三角形面积的综合运用.
1.如图1-1-10,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin ∠ABD的值是 ( )
D图1-1-10图1-1-11图1-1-12
【解析】 已知面积,要求tan C的值,应作高,构造直角三角形.
解: 过A作AD⊥BC于D,∵∠B=60°,
∴∠BAD=30°,∴AB∶BD=2∶1,
又∵AB∶BC=2∶5,
∴AB∶BD∶BC=2∶1∶5,【点悟】 求锐角的三角函数是以直角三角形为载体的,本题综合考查三角函数的定义、三角形的面积、勾股定理的运用.练 一 练
1.理解锐角三角函数的概念,并能将三角函数表示为 两条线段的比;
2.了解直角三角形中的两个锐角三角函数值之间的关 系;
3.了解直角三角形中的边与三角函数值的关系.
【学法指导】
1. 从定义出发,加强对三角函数的理解;
2.在求三角函数值的过程中,体会数形结合的思想方 法.填 一 填
1.锐角三角函数的概念
对于每一个确定的锐角α,在角一边上任取一点B,作BC⊥AC于点C,如图1-1-1所示,有:
三角函数:锐角α的___________________统称为角α的三角函数.【知识管理】图1-1-1正弦、余弦、正切2.直角三角形中的边角关系
范围:______
公式:当∠A+∠B=90°时,sin A=_________;
tan A·tan B=______.cos B1
1.(知识点2)如图1-1-2,在Rt△ABC中,∠C=90°,三边分别为a,b,c,则cos A等于 ( )【对点自测】D图1-1-22.(知识点1)如图1-1-3所示,△ABC的三个顶点分别在正方形网格的格点上,则tan A的值是 ( )图1-1-3A2图1-1-46研 一 研类型之一 求直角三角形中锐角的三角函数值
例1 如图1-1-5所示,Rt△ABC中,∠C=90°,AC=8,BC=6,求sin A,cos A,tan B的值.图1-1-5【点悟】 运用三角函数的定义解题是在直角三角形中进行的,因此通常先运用勾股定理求未知边,从而求三角函数值. 1.在Rt△ABC中,∠C=90°,AB=4,AC=1,则cos A的值是 ( )B2.在Rt△ABC中,∠C=90°,AC=5,AB=13,
则tan A+tan B=________.
3.如图1-1-6所示,在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若b=2a,则tan
A=____.
图1-1-6类型之二 已知直角三角形中的一锐角三角函数值,求这一锐角的其他三角函数值
(1)求出∠A,∠B的其他三角函数值;
(2)比较结果,你有什么发现?
图1-1-7【解析】 本题不能直接求出边长,但在Rt△ABC中给出了cos A的值,而要求的其他三角函数值是一个比值,故设AC=3k,AB=4k,可由勾股定理求出BC,从而达到目的.【点悟】(1)求一个锐角的三角函数值,关键是理解其意义,不需要求直角三角形各边之长,只知道它们的比值,同样可求出其他三角函数值.(2)知道比值往往设比值,即用k表示各边之长,这种转化的思想要掌握. 1.如图1-1-8所示,图(1)是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图(2),那么在Rt△ABC中,sin B的值是
( )B图1-1-8A类型之三 求非直角三角形中的三角函数值
例3 如图1-1-9所示,在△ABC中,AB=15,AC=13,S△ABC=84,求sin A的值.
【解析】 求sin A的值,由正弦定义可知,必须构造直角三角形,已知三角形面积,故作CD⊥AB于D,可解决问题.图1-1-9【点悟】 作三角形一边上的高,构造直角三角形是利用三角函数值解非直角三角形的常用方法,此题考查三角函数与三角形面积的综合运用.
1.如图1-1-10,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin ∠ABD的值是 ( )
D图1-1-10图1-1-11图1-1-12
【解析】 已知面积,要求tan C的值,应作高,构造直角三角形.
解: 过A作AD⊥BC于D,∵∠B=60°,
∴∠BAD=30°,∴AB∶BD=2∶1,
又∵AB∶BC=2∶5,
∴AB∶BD∶BC=2∶1∶5,【点悟】 求锐角的三角函数是以直角三角形为载体的,本题综合考查三角函数的定义、三角形的面积、勾股定理的运用.练 一 练
