2.3 等腰三角形的性质定理(2)

课件35张PPT。新浙教版数学八年级（上）2.3 等腰三角形的性质定理(2) （1）等腰三角形的一个内角为100°，
求其余各角。（2）等腰三角形的一个内角为40°，
求其余各角。（3）等腰三角形的一个内角为60°，
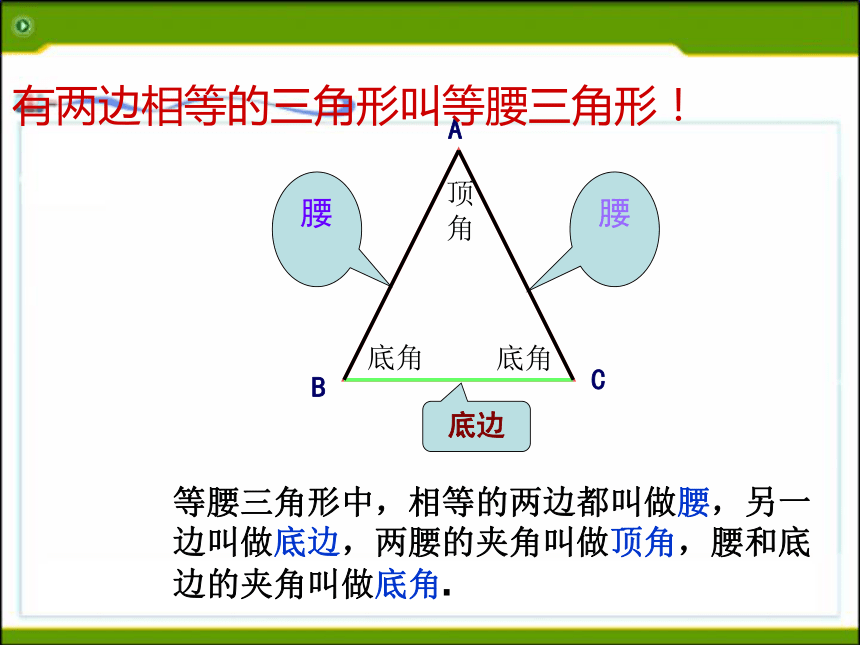
求其余各角。40°和40°40°和100°或70°和70°60°和60°回顾旧知、掌握新知底边底角底角顶角等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形！
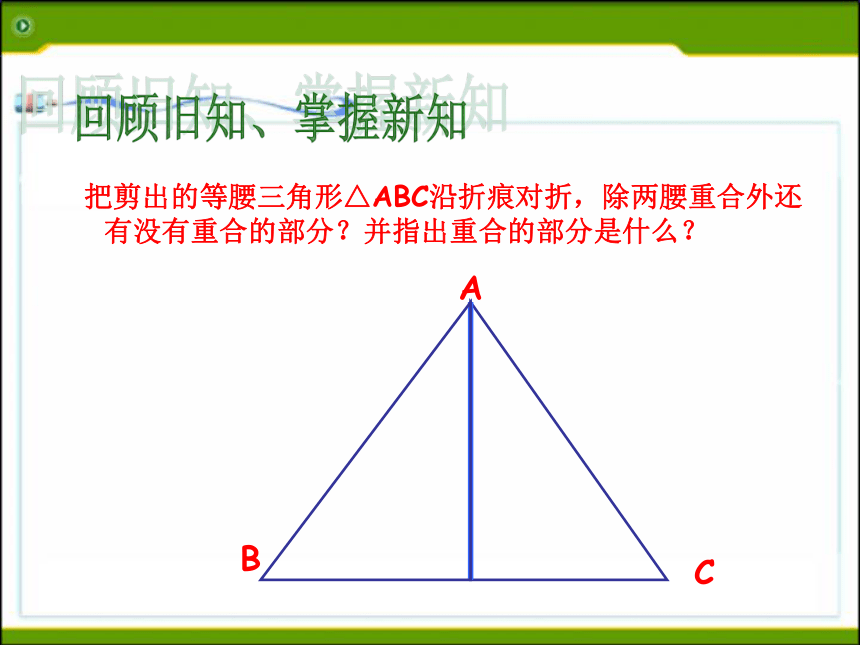
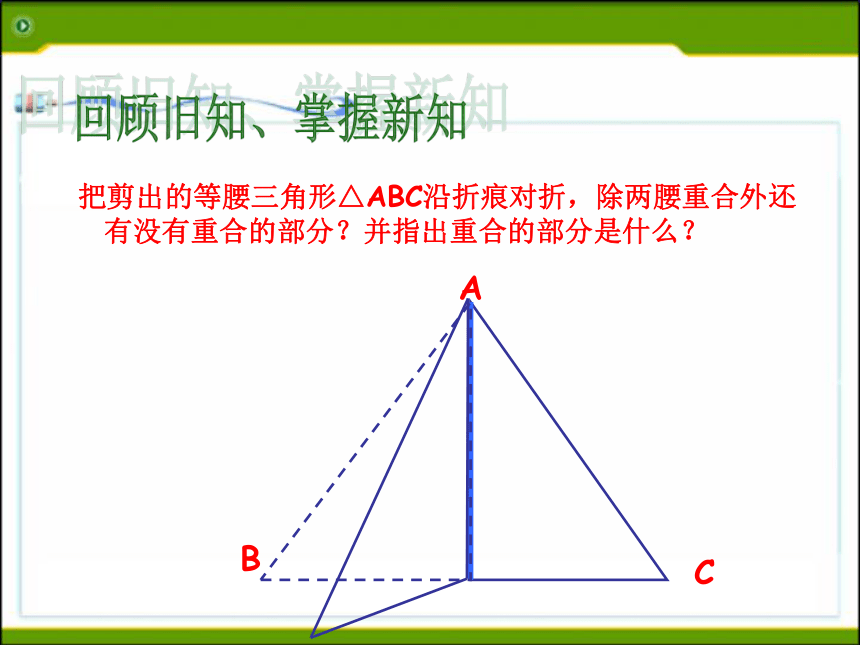
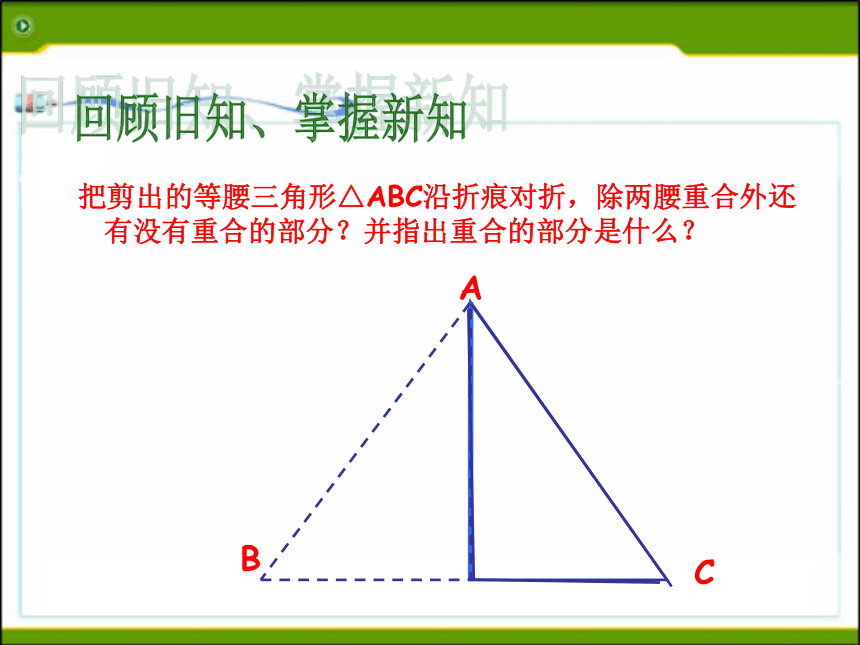
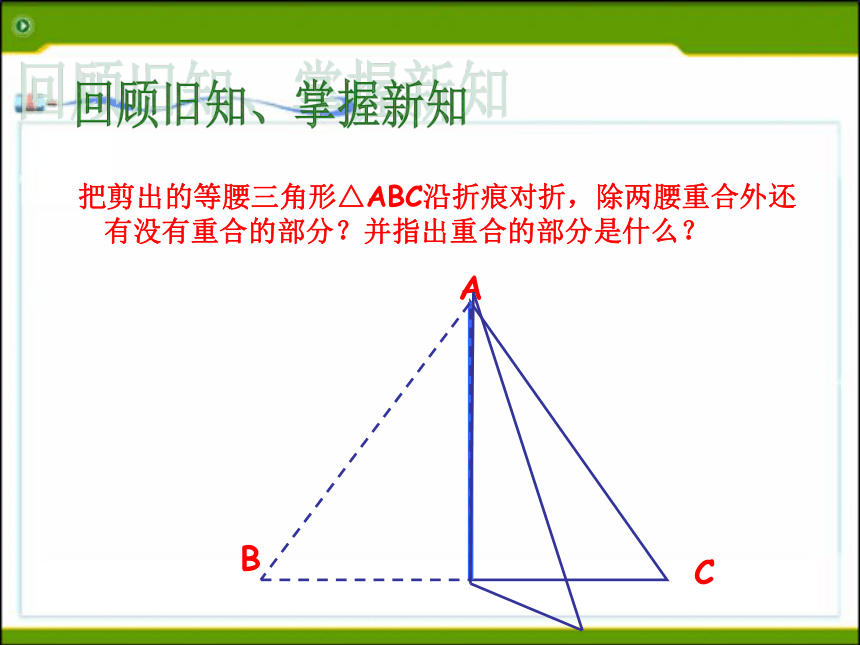
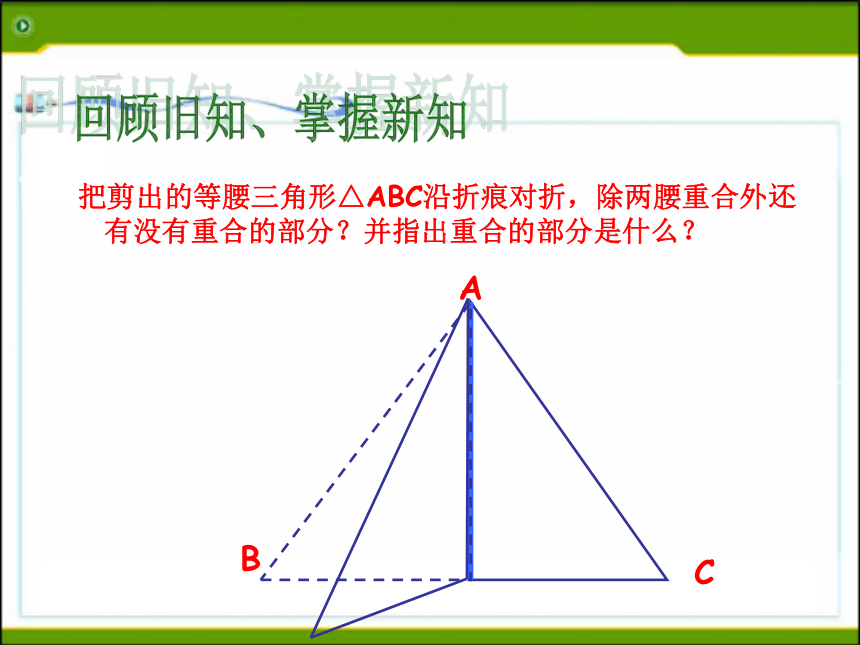
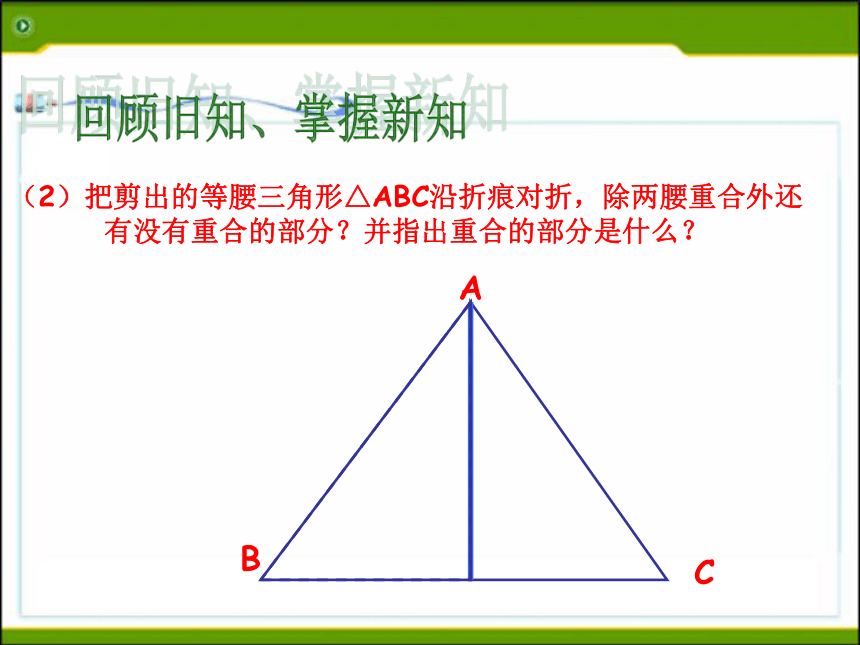
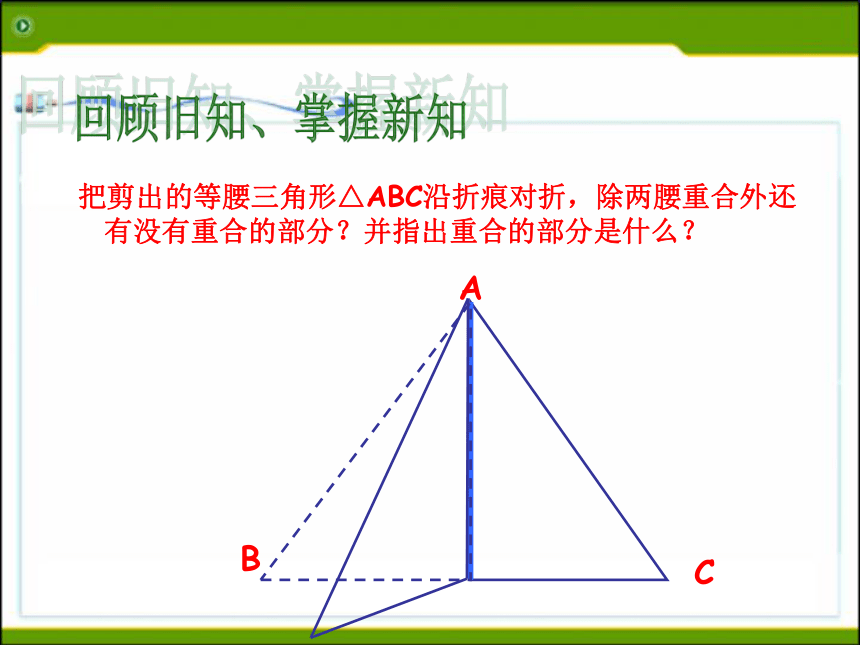
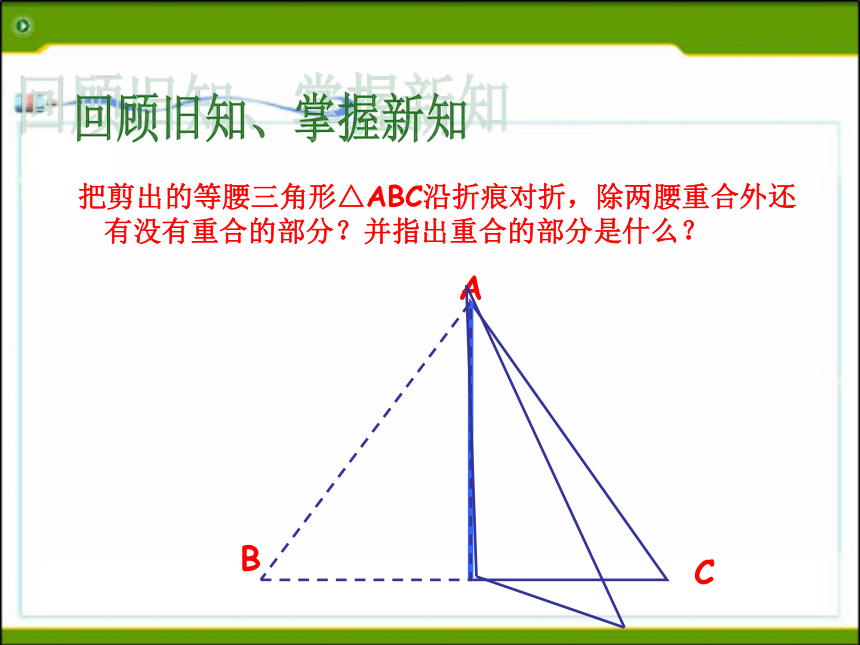
等腰三角形的性质:1 .等腰三角形的两个底角相等 （简写“等边对等角”）回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC（2）把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知ABC 把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 回顾旧知、掌握新知AC把剪出的等腰三角形△ABC沿折痕对折，除两腰重合外还有没有重合的部分？并指出重合的部分是什么？ 底角回顾旧知、掌握新知性质2：等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合。（通常说成等腰三角形的“三线合一”）性质2可分解成下面三个方面来理解：1、等腰三角形的顶角的平分线，既是底边上的中线，又是底边上的高。应用格式：∵AB＝AC ∠1＝∠2（已知）
∴BD＝DC AD⊥BC（等腰三角形三线合一）2、等腰三角形的底边上中线，既是底边上的高，又是顶角平分线。应用格式：∵AB＝AC BD＝DC （已知）
∴AD⊥BC ∠1＝∠2 （等腰三角形三线合一）
3、等腰三角形的底边上的高，既是底边上的中线，又是顶角平分线。应用格式：∵AB＝AC AD⊥BC （已知）
∴BD＝DC ∠1＝∠2 （等腰三角形三线合一）
ABCD21文字叙述几何语言等腰三角形的两底角相等（简称等边对等角）∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边（简称三线合一）①∵AB=AC，∠1=∠2 ∴AD⊥BC，BD=CD你掌握了吗？②∵AB=AC， AD⊥BC ∴ ∠1=∠2 ，BD=CD③∵AB=AC， BD=CD ∴ ∠1=∠2 ， AD⊥BC初步尝试例1 求证:等腰三角形两底角的平分线相等.证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵∠1= ∠ABC,∠2=　∠ACB(已知),
∴∠1=∠2(等式性质).
在△BDC与△CEB中
∵∠DCB=∠ EBC（已知）,
　BC=CB（公共边）,
　∠1=∠2（已证）,
∴△BDC≌△CEB（ASA）.
∴BD=CE(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.
求证:BD=CE.求证:等腰三角形两腰上的中线相等.证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵CM= AC,BN=　AB(已知),
∴CN=BM(等式性质).
在△BMC与△CNB中
∵ BC=CB（公共边）,
∠MCB=∠NBC（已知）,
　CM=BN（已证）,
∴△BMC≌△CNB（SAS）.
∴BM=CN(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.
求证:BM=CN.求证:等腰三角形两腰上的高相等.证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
又∵ BP,CQ是△ABC两腰上的高(已知),
∴∠BPC=∠CQB=900(高的意义).
在△BPC与△CQB中
∵∠BPC=∠CQB（已证）,
　 ∠PCB=∠QBC（已证）,
BC=CB（公共边）,
∴△BPC≌△CQB（AAS）.
∴BP=CQ(全等三角形的对应边相等)已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.
求证:BP=CQ.△ABC中，AB＝AC，D是BC边上的中点，
DF⊥AC于F DE ⊥ AB 于E .求证：DE＝DF。ABCDEF方法一：证明： ∵DE⊥AB，DF⊥AC（已知）
∴∠BED＝∠CFD
又∵D是BC中点（已知）
∴BD＝DC
∵AB＝AC（已知）
∴∠B＝∠C（等边对等角）
在△DBE与△DCF中
∠DEB＝∠DFC（已证）
∠B＝∠C（已证）
BD＝DC（已证）
∴ △BDE ≌ △CDF（AAS）
∴DE＝DF 方法二：连AD 。
∵AB＝AC，BD＝DC（已知）
∴AD是∠BAC的平分线。
（等腰三角形三线合一）
又∵DE⊥AB DF⊥AC
∴DE＝DF
（角平分线上的点到这个
角的两边距离相等）
5、已知线段a, h(如图),用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.作法文字叙述几何语言等腰三角形的两底角相等（简称等边对等角）∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边（简称三线合一）①∵AB=AC，∠1=∠2 ∴AD⊥BC，BD=CD你清楚了吗？②∵AB=AC， AD⊥BC ∴ ∠1=∠2 ，BD=CD③∵AB=AC， BD=CD ∴ ∠1=∠2 ， AD⊥BC当堂巩固练一练判断下列语句是否正确。（1）等腰三角形的角平分线、中线和高线互相重合。（ ）
（2）有一个角是60°的等腰三角形，其它两个
内角也为60°. （ ）
（3）等腰三角形的底角都是锐角. （ ）
（4）钝角三角形不可能是等腰三角形 . （ ）××填空：在△ABC中，AB＝AC， D 在BC上，
1、如果AD⊥BC，那么∠BAD = ∠______,
BD = ______
2、如果∠BAD= ∠CAD，那么AD⊥___, BD = ____
3、如果BD=CD,那么∠BAD =∠ _____， AD⊥___,
∠ADB =∠ _____=___°DCADCDBCCDCADBCADC90如图，在△ABC中，AB=AC，D是BC边上的中点，∠B=30。.求∠１和∠ADC的度数．∵ AB=AC，D是BC边上的中点∠ADC＝ 90°∵ ∠BAC=180°-30°-30°=120°（三线合一） 如图：△ABC中，AB=AC,AD和BE是高，它们相交于点H，且AE=BE。 求证：AH=2BD
证明：∵AB=AC,AD是高(已知)∴BC=2BD（三线合一）又∵BE是高（已知）∴∠ADC=∠BEC=∠AEH=90°（垂直的定义）在△AEH和△BEC中∴△AEH≌△BEC(ASA)∴∠1+∠C=∠2+∠C=90°∴ ∠1=∠2（同角的余角相等） ∴AH=BC（全等三角形的性质）∴AH=2BD（等量代换）巩固挑战D作△ABC的中线AD，交底边BC于D。 D┌作△ABC的高AD，垂直底边BC于D。D作顶角的平分线AD.等腰三角形常见辅助线自我挑战1.如图：在三角形ABC中，AB=AC ， D在 AC上，且BD=BC=AD，求△ABC各内角的度数？讨论：2、∠A与哪些角相等？1、∠C与哪些角相等？（∠3、 ∠ABC ）123（ ∠1、 ∠2 ）3、 ∠C与∠A是什么关系？（ ∠C=2 ∠A ）解：∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720拓展提高∵AB=AC，∠1=∠2
∴________________AD⊥BC或BD=CD∵AB=AC，AD⊥BC
∴________________∠1=∠2 或BD=CD∵AB=AC，
∴∠1=∠2 或 AD⊥BC 等腰三角形“三线合一”的性质
几何语言：__________BD=CD思考题： 如图所示，已知下列两个
三角形，思考怎样把每个三角形只剪一次，将它分成两个等腰三角形？试一试，你一定会成功的。课堂小结等腰三角形概念性质等边对等角三线合一有两边相等的三角形腰、底、顶角、底角谢谢大家！