第2章 特殊三角形专题培优:直角三角形(例题+巩固练习+解析)
文档属性
| 名称 | 第2章 特殊三角形专题培优:直角三角形(例题+巩固练习+解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四讲:直角三角形
一.例题
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠1=30°,BD=2,则AD的长为( )
A.4 B.6 C.8 D.10
2.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A﹣∠B=∠C
C.a2﹣b2=c2 D.a:b:c=7:24:25
第1题 第3题 第4题 第5题
3.如图是边长为1的3×3的正方形网格,已知△ABC的三个顶点均在正方形格点上,则BC边上的高是( )
A. B. C.2 D.
4.如图,在△ABC中,∠ACB=90°,点D在AC边上且AD=BD,M是BD的中点,若AC=16,BC=8,则CM等于( )www-2-1-cnjy-com
A.5 B.6 C.8 D.10
5.如图,在同一水平线上有相距8m的两棵树AB和CD,其中树AB高8m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )【版权所有:21教育】
A.6m B.5m C.4m D.3m
6.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,E是BD的中点,BD=8,则△AEC的面积为( )21*cnjy*com
A. B.16 C.8 D.
第7题 第8题 第9题
7.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= .
8.如图,AB=BC且AB⊥BC,点P为线段BC上一点,PA⊥PD且PA=PD,若∠A=26°,则∠D的度数为 .
9.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 .
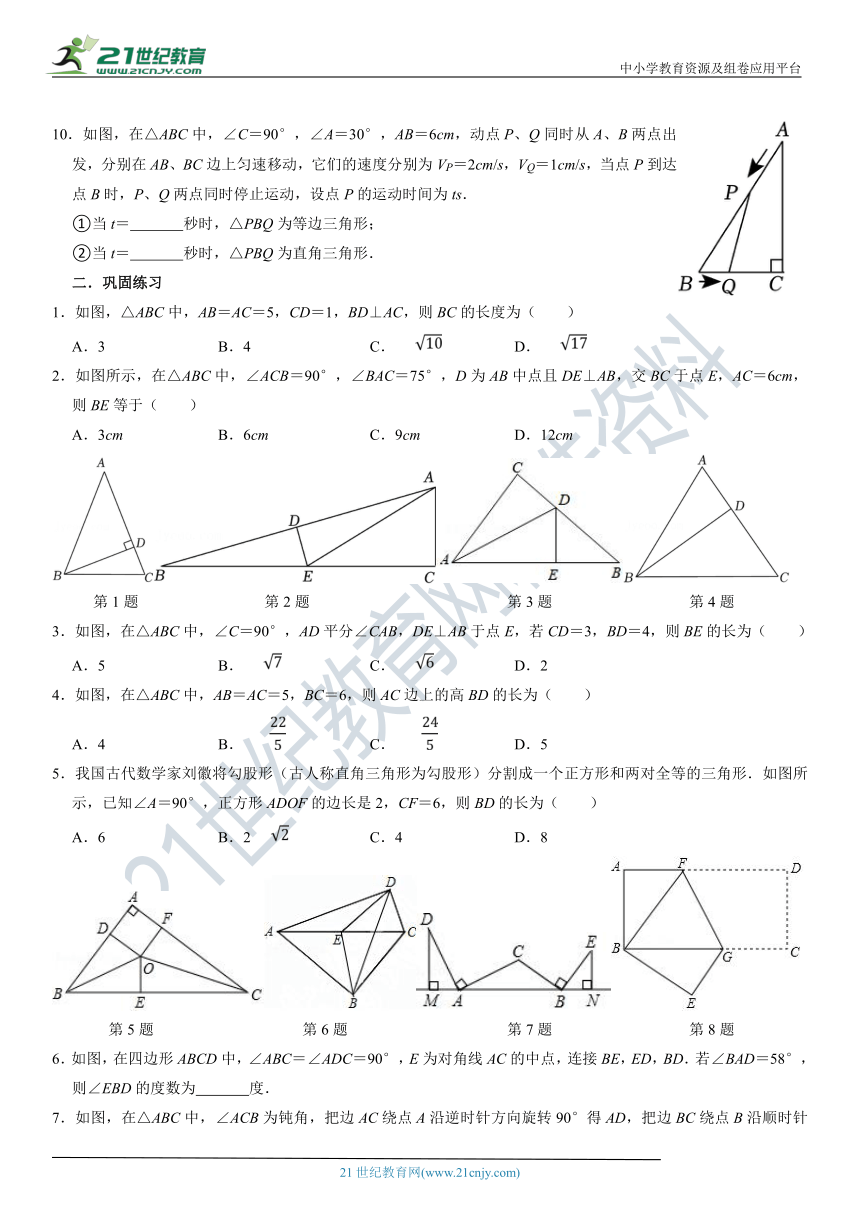
10.如图,在△ABC中,∠C=90°,∠A=30°,AB=6cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
①当t= 秒时,△PBQ为等边三角形;
②当t= 秒时,△PBQ为直角三角形.
二.巩固练习
1.如图,△ABC中,AB=AC=5,CD=1,BD⊥AC,则BC的长度为( )
A.3 B.4 C. D.
2.如图所示,在△ABC中,∠ACB=90°,∠BAC=75°,D为AB中点且DE⊥AB,交BC于点E,AC=6cm,则BE等于( )
A.3cm B.6cm C.9cm D.12cm
第1题 第2题 第3题 第4题
3.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若CD=3,BD=4,则BE的长为( )
A.5 B. C. D.2
4.如图,在△ABC中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
A.4 B. C. D.5
5.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知∠A=90°,正方形ADOF的边长是2,CF=6,则BD的长为( )
A.6 B.2 C.4 D.8
第5题 第6题 第7题 第8题
6.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为 度.
7.如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM= .
8.如图,在矩形ABCD中,AB=6,BC=18,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为 .
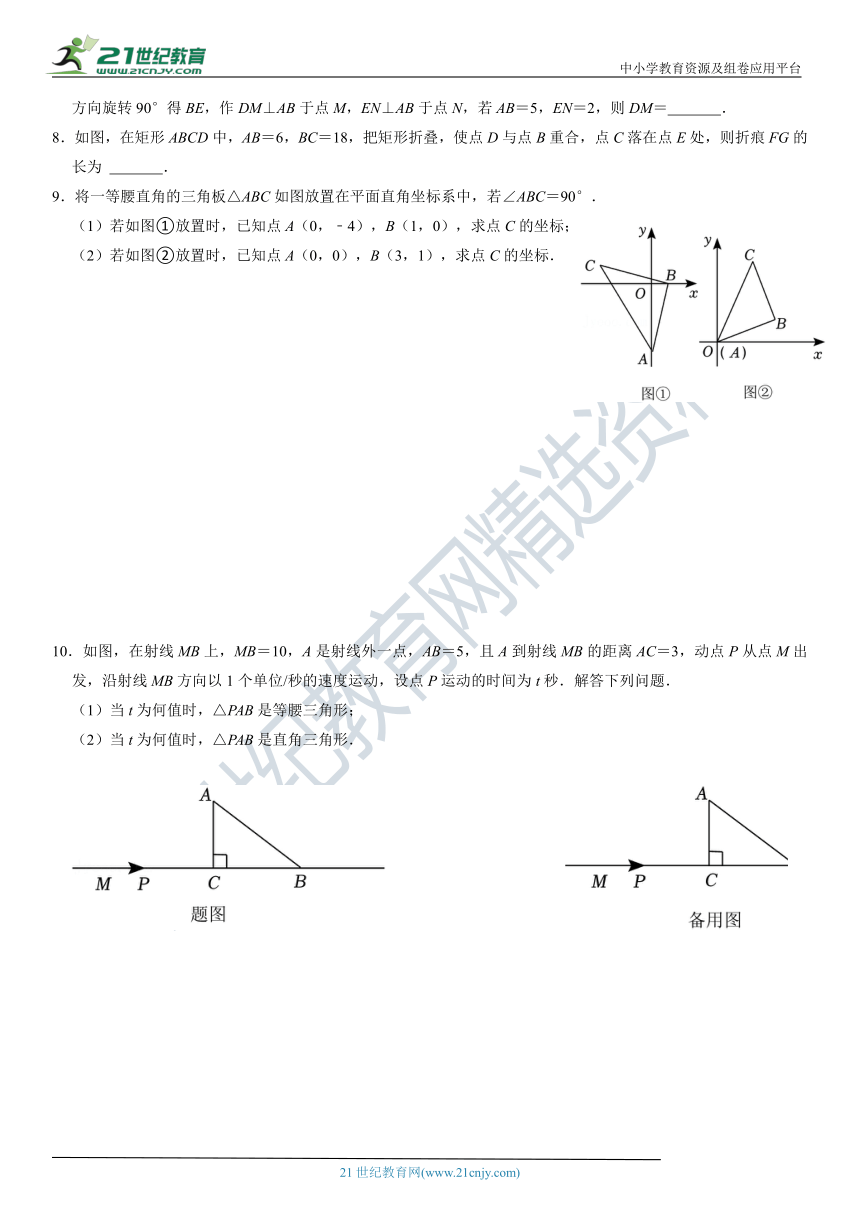
9.将一等腰直角的三角板△ABC如图放置在平面直角坐标系中,若∠ABC=90°.
(1)若如图①放置时,已知点A(0,﹣4),B(1,0),求点C的坐标;
(2)若如图②放置时,已知点A(0,0),B(3,1),求点C的坐标.
10.如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.
(1)当t为何值时,△PAB是等腰三角形;
(2)当t为何值时,△PAB是直角三角形.
八上培优专题:直角三角形
参考答案与试题解析
一.试题(共25小题)
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠1=30°,BD=2,则AD的长为( )
A.4 B.6 C.8 D.10
【分析】根据垂直定义可得∠CDB=90°,再在Rt△CBD中,利用含30度角的直角三角形的性质可得BC=4,∠B=60°,然后利用直角三角形的两个锐角互余可得∠A=30°,再在Rt△ABC中,利用含30度角的直角三角形的性质可得AB=8,最后利用线段的和差关系进行计算即可解答.
【解答】解:∵CD⊥AB,
∴∠CDB=90°,
∵∠1=30°,BD=2,
∴BC=2BD=4,∠B=90°﹣∠1=60°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=30°,
∴AB=2BC=8,
∴AD=AB﹣BD=8﹣2=6,
故选:B.
【点评】本题考查了含30度角的直角三角形,熟练掌握含30度角的直角三角形的性质是解题的关键.
2.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A﹣∠B=∠C
C.a2﹣b2=c2 D.a:b:c=7:24:25
【分析】根据三角形内角和定理以及勾股定理即可求出答案.
【解答】解:A、设∠A=3x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴x=15°,
∴∠C=75°,故不能成立;
B、∵∠A=∠B+∠C,
∠A+∠B+∠C=180°,
∴∠A=90°,故能成立;
C、当∠A=90°时,此时a2=b2+c2,故能成立;
D、设a=7x,b=24x,c=25x,
当∠C=90°,
∴a2+b2=c2,故能成立.
故选:A.
【点评】本题考查勾股定理,解题的关键是熟练运用勾股定理,本题属于基础题型.
3.如图是边长为1的3×3的正方形网格,已知△ABC的三个顶点均在正方形格点上,则BC边上的高是( )
A. B. C.2 D.
【分析】先根据勾股定理分别求出AB,AC,BC的长,根据勾股定理逆定理判断出△ABC是直角三角形,再根据三角形的面积公式即可求解.21·cn·jy·com
【解答】解:∵AB,
AC,
BC,
∴AB2+AC2=BC2=10,
∴△ABC是直角三角形,
设BC边上的高为h,
则S,
∴h,
即BC边上的高是,
故选:A.
【点评】本题考查了勾股定理以及勾股定理逆定理,三角形的面积公式,判断出△ABC是直角三角形是解题的关键.2·1·c·n·j·y
4.如图,在△ABC中,∠ACB=90°,点D在AC边上且AD=BD,M是BD的中点,若AC=16,BC=8,则CM等于( )
A.5 B.6 C.8 D.10
【分析】根据勾股定理得出BD,进而利用直角三角形的性质解答即可.
【解答】解:设BD=x,则CD=AC﹣AD=AC﹣BD=16﹣x,
在Rt△BCD中,由勾股定理得:BD2=BC2+CD2,
即:x2=82+(16﹣x)2,
解得:x=10,
∴BD=10,
∵M是BD的中点,
∴CM=5,
故选:A.
【点评】此题考查勾股定理,关键是根据勾股定理得出BD解答.
5.如图,在同一水平线上有相距8m的两棵树AB和CD,其中树AB高8m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )【来源:21cnj*y.co*m】
A.6m B.5m C.4m D.3m
【分析】根据题意表示出AE=4m,设AF=xm,则EF=(8﹣x) m,再利用勾股定理得出答案.
【解答】解:如图所示:根据题意可得,AE=4m,设AF=xm,则EF=(8﹣x) m,
在Rt△AEF中,
AF2+AE2=EF2,
即x2+42=(8﹣x)2,
解得:x=3,
树的折断点离地面的高度是3m.
故选:D.
【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.
6.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,E是BD的中点,BD=8,则△AEC的面积为( )
A. B.16 C.8 D.
【分析】由直角三角形斜边上中线的性质可求E=CE=4,利用三角形外角的性质结合等腰三角形的性质可求解∠AEC=90°,再利用三角形的面积公式计算可求解.
【解答】解:∵∠BAD=∠BCD=90°,E是BD的中点,BD=8,
∴AE=CEBD=4,
∴∠ABE=∠BAE,∠CBE=∠BCE,
∵∠AED=∠ABE+∠BAE=2∠ABE,∠CED=∠CBE+∠BCE=2∠CBE,
∴∠AEC=2∠ABE+2∠CBE=2∠ABC,
∵∠ABC=45°,
∴∠AEC=90°,
∴S△ACEAE CE4÷4=8.
故选:C.
【点评】本题主要考查三角形斜边上的中线的性质,三角形外交的性质,三角形的面积,求解AE,CE的长及∠AEC=90°可求解△ACB的面积.
7.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= 6 .
【分析】设BC=x,AF可用含x的式子表示,CF可以根据勾股定理求出,然后用x表示出BF,在Rt△ABF中,利用勾股定理,可建立关于x的方程,即可得出BF的长.
【解答】解:由折叠的性质知:AD=AF,DE=EF=8﹣3=5;
在Rt△CEF中,EF=DE=5,CE=3,由勾股定理可得:CF=4,
若设AD=AF=x,则BC=x,BF=x﹣4;
在Rt△ABF中,由勾股定理可得:
82+(x﹣4)2=x2,解得x=10,
故BF=x﹣4=6.
故答案为:6.
【点评】考查了勾股定理的应用,综合能力要求较高.同时也考查了列方程求解的能力.
8.如图,AB=BC且AB⊥BC,点P为线段BC上一点,PA⊥PD且PA=PD,若∠A=26°,则∠D的度数为 19° .
【分析】如图,作DH⊥BC交BC的延长线于H.只要证明△ABP≌△PHD(AAS),得出AB=PH,PB=DH,∠A=∠DPH=26°,由AB=CB,推出BC=PH,推出PB=CH=DH,可得∠DCH=45°即可解决问题.
【解答】解:如图,作DH⊥BC交BC的延长线于H.
∵AB⊥BC,DH⊥BC,PA⊥PD,
∴∠B=∠APD=∠H=90°,
∴∠A+∠APB=90°,∠APB+∠DPH=90°,
∴∠A=∠DPH,
∵PA=PD.
∴△ABP≌△PHD(AAS),
∴AB=PH,PB=DH,∠A=∠DPH=26°,
∵AB=CB,
∴BC=PH,
∴PB=CH=DH,
∴∠DCH=45°,
∵∠DCH=∠DPC+∠PDC,
∴∠PDC=19°.
故答案为:19°.
【点评】本题考查全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是添加常用辅助线,构造全等三角形解决问题.www.21-cn-jy.com
9.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 2 .21教育名师原创作品
【分析】作辅助线GH过点E,且GH∥AB,构造一线三垂直模型,用EH分别表示出S1和S2的值,列出关于EH的式子,求出EH即可求出CE.
【解答】解:如图,作GH过点E,且GH∥AB,
∵∠HBE+∠HEB=90°,∠HEB+∠GEF=90°,
∴∠HBE=∠GEF,
∵AC为正方形的对角线,
∴CH=EH,
∴HB=GE,
在△HBE和△GEF中,
,
∴△HBE≌△GEF(ASA),
∴GF=EH,
设EH=a,AF=6﹣2a,
,,
∵2S1=3S2,
∴6a=3(a2﹣9a+18),
解得a=2,
∴CE2,
故答案为2.
【点评】本题主要考查正方形的性质和全等三角形的判定,关键是要能作出辅助线GH,构造一线三垂直模型,出现需要判定的全等三角形,将AF用EH表示出来.2-1-c-n-j-y
10.如图,在△ABC中,∠C=90°,∠A=30°,AB=6cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
①当t= 2 秒时,△PBQ为等边三角形;
②当t= 1.5或 秒时,△PBQ为直角三角形.
【分析】(1)由题意得AP=2tcm,BQ=tcm,BP=AB AP=(6 2t)cm,再由等边三角形的性质得到PB=BQ,即6 2t=t,解方程即可;
(2)讨论∠PQB=90°或∠BPQ=90°时,利用PB与BQ之间的关系,建立方程求解即可.
【解答】解:(1)∵∠C=90°,∠A=30°,AB=8cm,
∴∠B=60°,
∴当PB=BQ时,△PBQ是等边三角形,
由题意得AP=2tcm,BQ=tcm,
∴BP=AB AP=(6 2t)cm,
∴6 2t=t,
解得t=2,
∴当t=2时,△PBQ为等边三角形;
故答案为:2.
(2)∵∠C=90°,∠A=30°,
∴∠B=60°,
∴当△PBQ为直角三角形时,只能是∠PQB=90°或∠BPQ=90°,
当∠PQB=90°时,如图,
∴∠BPQ=30°,
∴BQBP,
∵BP=(6 2t)cm,BQ=tcm,
∴t(6 2t),
解得t=1.5;
当∠BPQ=90°时,如图,
∴∠PQB=30°,
∴BQ=2BP,
∴t=2(6 2t),
解得t,
综上所述,当t=1.5或t时△PBQ为直角三角形.
故答案为:1.5或.
【点评】本题主要考查了等边三角形的判定,含30度角的直角三角形的性质、解一元一次方程,解题的关键在于能够熟练掌握含30度角的直角三角形的性质.21教育网
11.如图,△ABC中,AB=AC=5,CD=1,BD⊥AC,则BC的长度为( )
A.3 B.4 C. D.
【分析】先根据勾股定理求出BD,再根据勾股定理求出BC.
【解答】解:∵AC=5,CD=1,
∴AD=5﹣1=4,
在Rt△ABD中,BD3,
在Rt△BCD中,BC,
故选:C.
【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
12.如图所示,在△ABC中,∠ACB=90°,∠BAC=75°,D为AB中点且DE⊥AB,交BC于点E,AC=6cm,则BE等于( )21cnjy.com
A.3cm B.6cm C.9cm D.12cm
【分析】先利用直角三角形的两个锐角互余可得∠B=15°,再利用线段垂直平分线的性质可得EA=EB,从而可得∠B=∠BAE=15°,然后利用三角形的外角性质可得∠AEC=30°,再在Rt△AEC中,利用含30度角的直角三角形可求出AE的长,即可解答.【来源:21·世纪·教育·网】
【解答】解:∵∠ACB=90°,∠BAC=75°,
∴∠B=90°﹣∠BAC=15°,
∵D为AB中点且DE⊥AB,
∴DE是AB的垂直平分线,
∴EA=EB,
∴∠B=∠BAE=15°,
∴∠AEC=∠B+∠BAE=30°,
∵AC=6cm,
∴AE=2AC=12(cm),
∴BE=AE=12cm,
故选:D.
【点评】本题考查了含30度角的直角三角形,线段垂直平分线的性质,熟练掌握含30度角的直角三角形,以及线段垂直平分线的性质是解题的关键.
13.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若CD=3,BD=4,则BE的长为( )
A.5 B. C. D.2
【分析】利用角平分线的性质得DE=CD=3,再利用勾股定理求出BE即可.
【解答】解:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DE=CD=3,
∵BD=4,
∴BE,
故选:B.
【点评】本题主要考查了角平分线的性质,勾股定理等知识,熟练掌握角平分线的性质和勾股定理是解题的关键.
14.如图,在△ABC中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
A.4 B. C. D.5
【分析】过A作AE⊥BC于点E,根据勾股定理计算出底边上的高AE的长,然后计算三角形的面积,再以AC为底,利用三角形的面积计算出AC边上的高BD即可.【出处:21教育名师】
【解答】解:过A作AE⊥BC于点E,
∵AB=AC,
∴△ABC是等腰三角形,
∵AE⊥BC,
∴EB=ECCB=3,
在Rt△ABE中,AE4,
∴S△ABC AC BD BC AE6×4=12,
∴5×BD=12,
解得BD.
故选:C.
【点评】此题主要考查了勾股定理的应用,以及等腰三角形的性质,关键是掌握等腰三角形底边上的高和中线重合.
15.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知∠A=90°,正方形ADOF的边长是2,CF=6,则BD的长为( )
A.6 B.2 C.4 D.8
【分析】设BD=x,正方形ADOF的边长为2,则AD=AF=2,根据全等三角形的性质得到CF=CE,BE=BD,根据勾股定理即可得到结论.
【解答】解:正方形ADOF的边长为2,则AD=AF=2,
设BD=x,
∵△BDO≌△BEO,△CEO≌△CFO,
∴BD=BE,CF=CE,
∴AB=x+2,AC=6+2=8,BC=x+6,
∵AC2+AB2=BC2,
∴(x+2)2+82=(x+6)2,
∴x=4,
∴BD=4,
故选:C.
【点评】本题考查了勾股定理,全等三角形的性质,正方形的性质,熟练掌握勾股定理是解题的关键.
16.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为 32 度.21·世纪*教育网
【分析】根据已知条件得到点A,B,C,D在以E为圆心,AC为直径的同一个圆上,根据圆周角定理得到∠DEB=116°,根据直角三角形的性质得到DE=BEAC,根据等腰三角形的性质即可得到结论.
【解答】解:∵∠ABC=∠ADC=90°,
∴点A,B,C,D在以E为圆心,AC为直径的同一个圆上,
∵∠BAD=58°,
∴∠DEB=116°,
∵DE=BEAC,
∴∠EBD=∠EDB=32°,
故答案为:32.
【点评】本题考查了直角三角形斜边上的中线的性质,圆周角定理,推出A,B,C,D四点共圆是解题的关键.
17.如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM= 3 .
【分析】过点C作CF⊥AB于点F,由旋转的性质可得AD=AC,BE=BC,利用“一线三等角“证得∠D=∠CAF,从而可判定△DAM≌△ACF(AAS),则DM=AF.同理可证,△BFC≌△ENB(AAS),则BF=EN=2,再由AB=5,可得AF,即DM的值.
【解答】解:过点C作CF⊥AB于点F,如图所示:
∵旋转,
∴AD=AC,BE=BC,
∵DM⊥AB于点M,EN⊥AB于点N,CF⊥AB于点F,
∴∠AMD=∠AFC=∠BFC=∠BNE=90°,
∴∠D+∠DAM=90°,
∵∠CAD=90°,
∴∠CAF+∠DAM=90°,
∴∠D=∠CAF,
∴在△DAM和△ACF中,
,
∴△DAM≌△ACF(AAS),
∴DM=AF.
同理可证,△BFC≌△ENB(AAS),
∴BF=EN=2,
∵AB=5,
∴AF=3,
∴DM=3.
故答案为:3.
【点评】本题考查了旋转的性质、全等三角形的判定与性质等知识点,正确作出辅助线构造全等三角形是解题的关键.
18.如图,在矩形ABCD中,AB=6,BC=18,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为 2 .
【分析】连接BD,在Rt△ABD中,求得BD的长,在Rt△ADF中运用勾股定理求得DF的长,即可得到DF长,最后在Rt△DOF中求得FO的长,即可得到答案.
【解答】解:如图,连接BD,交FG于O,则由轴对称的性质可知,FG垂直平分BD,
Rt△ABD中,BD,
由折叠可得DOBD=3,∠BFO=∠DFO,
由AB∥CD可得,∠DFO=∠BGO,
∴∠DFO=∠BGO,
∴BF=BG,即△BFG是等腰三角形,
∴BD平分FG,
∴OF=OG,
由折叠知,BF=DF,
设BF=DF=x,则AF=18﹣x,
在Rt△ABF中,(18﹣x)2+62=x2,
解得x=10,即DF=10,
∴Rt△DOF中,OF,
∴FG=2FO=2.
故答案为:2.
【点评】本题是折叠问题,主要考查了折叠的性质,勾股定理以及矩形的性质的综合应用,解决问题的关键是根据勾股定理列方程求解.21世纪教育网版权所有
19.将一等腰直角的三角板△ABC如图放置在平面直角坐标系中,若∠ABC=90°.
(1)若如图①放置时,已知点A(0,﹣4),B(1,0),求点C的坐标;
(2)若如图②放置时,已知点A(0,0),B(3,1),求点C的坐标.
【分析】(1)过点C作x轴的垂线,交x轴于点D,再利用边角关系证明∴△BCD≌△ABO,求出CD=1,OD=3,即可得出答案;21*cnjy*com
(2)过B作x轴的垂线,交x轴于点D,过点C作DB的垂线交DB的延长线于点E,再利用边角关系证明△ABD≌△BCE,求出CE=1,DE=4,即可得出答案.
【解答】解:(1)过点C作x轴的垂线,交x轴于点D,
∵A(0,﹣4),B(1,0),
∴OA=4,OB=1,
∴∠ABC=90°,∠AOB=90°,
∴∠CBD+∠OBA=90°,∠OAB+∠OBA=90°,
∴∠CBD=∠BAO,
∵AB=BC,∠AOB=∠BDC=90°,
∴△BCD≌△ABO(AAS),
∴CD=BO=1,BD=AO=4,
∴OD=3,
∴点C坐标为(﹣3,1);
(2)过B作x轴的垂线,交x轴于点D,过点C作DB的垂线交DB的延长线于点E,
∵A(0,0),B(3,1),
∴OD=3,BD=1,
∵∠ABC=90°,∠ADB=90°,
∴∠CBE+∠OBD=90°,∠BAD+∠OBD=90°,
∴∠BAD=∠CBE,
∵AB=BC,∠ADB=∠BEC=90°,
∴△ABD≌△BCE(AAS),
∴CE=BD=1,BE=AD=3,
∴DE=4,
∴点C的横坐标为3﹣1=2,
∴点C坐标为(2,4).
【点评】本题考查全等三角形的判定与性质以及坐标与图形性质,利用全等三角形的判定定理证出三角形全等是解题关键.
20.如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.
(1)当t为何值时,△PAB是等腰三角形;
(2)当t为何值时,△PAB是直角三角形.
【分析】(1)先由勾股定理求出BC=4,再分三种情况进行讨论:①若BA=BP;②若AB=AP;③若PA=PB.分别列出方程求解即可;
(2)先由勾股定理求出,再分两种情况进行讨论:①当∠APB=90°时,点P与点C重合,则t=6;②当∠BAP=90°时,根据勾股定理列方程,求解即可.
【解答】解:(1)在Rt△ABC中,AB=5,AC=3,
由勾股定理可得BC=4.
由题意可得MP=t.
当△PAB是等腰三角形时,分三种情况:
①若BA=BP,如图1.
则有|10﹣t|=5,
解得t=5或15;
②若AB=AP,如图2.
则有PB=2BC,故有10﹣t=8,
解得t=2;
③若PA=PB,如图3.
则有,
解得.
综上,当t为5或15或2或时,△PAB是等腰三角形.
(2)由MP=t,BP=|10﹣t|,由勾股定理可得.
当△PAB是直角三角形时,分两种情况:
①当∠APB=90°时,如图4.
点P与点C重合,则t=6;
②当∠BAP=90°时,如图5.
则有,解得.
综上,当t为6或时,△PAB是直角三角形.
【点评】本题考查了勾股定理,等腰三角形的判定与性质,进行分类讨论是解题的关键.
声明:试题解析著作权属21世纪教育网所有,未经书面同意,不得复制发布日期:2023/1/24 21:29:03;用户:陈梦洁;邮箱:17858502426;学号:28029722
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四讲:直角三角形
一.例题
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠1=30°,BD=2,则AD的长为( )
A.4 B.6 C.8 D.10
2.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A﹣∠B=∠C
C.a2﹣b2=c2 D.a:b:c=7:24:25
第1题 第3题 第4题 第5题
3.如图是边长为1的3×3的正方形网格,已知△ABC的三个顶点均在正方形格点上,则BC边上的高是( )
A. B. C.2 D.
4.如图,在△ABC中,∠ACB=90°,点D在AC边上且AD=BD,M是BD的中点,若AC=16,BC=8,则CM等于( )www-2-1-cnjy-com
A.5 B.6 C.8 D.10
5.如图,在同一水平线上有相距8m的两棵树AB和CD,其中树AB高8m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )【版权所有:21教育】
A.6m B.5m C.4m D.3m
6.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,E是BD的中点,BD=8,则△AEC的面积为( )21*cnjy*com
A. B.16 C.8 D.
第7题 第8题 第9题
7.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= .
8.如图,AB=BC且AB⊥BC,点P为线段BC上一点,PA⊥PD且PA=PD,若∠A=26°,则∠D的度数为 .
9.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 .
10.如图,在△ABC中,∠C=90°,∠A=30°,AB=6cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
①当t= 秒时,△PBQ为等边三角形;
②当t= 秒时,△PBQ为直角三角形.
二.巩固练习
1.如图,△ABC中,AB=AC=5,CD=1,BD⊥AC,则BC的长度为( )
A.3 B.4 C. D.
2.如图所示,在△ABC中,∠ACB=90°,∠BAC=75°,D为AB中点且DE⊥AB,交BC于点E,AC=6cm,则BE等于( )
A.3cm B.6cm C.9cm D.12cm
第1题 第2题 第3题 第4题
3.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若CD=3,BD=4,则BE的长为( )
A.5 B. C. D.2
4.如图,在△ABC中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
A.4 B. C. D.5
5.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知∠A=90°,正方形ADOF的边长是2,CF=6,则BD的长为( )
A.6 B.2 C.4 D.8
第5题 第6题 第7题 第8题
6.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为 度.
7.如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM= .
8.如图,在矩形ABCD中,AB=6,BC=18,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为 .
9.将一等腰直角的三角板△ABC如图放置在平面直角坐标系中,若∠ABC=90°.
(1)若如图①放置时,已知点A(0,﹣4),B(1,0),求点C的坐标;
(2)若如图②放置时,已知点A(0,0),B(3,1),求点C的坐标.
10.如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.
(1)当t为何值时,△PAB是等腰三角形;
(2)当t为何值时,△PAB是直角三角形.
八上培优专题:直角三角形
参考答案与试题解析
一.试题(共25小题)
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠1=30°,BD=2,则AD的长为( )
A.4 B.6 C.8 D.10
【分析】根据垂直定义可得∠CDB=90°,再在Rt△CBD中,利用含30度角的直角三角形的性质可得BC=4,∠B=60°,然后利用直角三角形的两个锐角互余可得∠A=30°,再在Rt△ABC中,利用含30度角的直角三角形的性质可得AB=8,最后利用线段的和差关系进行计算即可解答.
【解答】解:∵CD⊥AB,
∴∠CDB=90°,
∵∠1=30°,BD=2,
∴BC=2BD=4,∠B=90°﹣∠1=60°,
∵∠ACB=90°,
∴∠A=90°﹣∠B=30°,
∴AB=2BC=8,
∴AD=AB﹣BD=8﹣2=6,
故选:B.
【点评】本题考查了含30度角的直角三角形,熟练掌握含30度角的直角三角形的性质是解题的关键.
2.已知Rt△ABC的三边分别为a、b、c,则下列结论不可能成立的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A﹣∠B=∠C
C.a2﹣b2=c2 D.a:b:c=7:24:25
【分析】根据三角形内角和定理以及勾股定理即可求出答案.
【解答】解:A、设∠A=3x,∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,
∴x=15°,
∴∠C=75°,故不能成立;
B、∵∠A=∠B+∠C,
∠A+∠B+∠C=180°,
∴∠A=90°,故能成立;
C、当∠A=90°时,此时a2=b2+c2,故能成立;
D、设a=7x,b=24x,c=25x,
当∠C=90°,
∴a2+b2=c2,故能成立.
故选:A.
【点评】本题考查勾股定理,解题的关键是熟练运用勾股定理,本题属于基础题型.
3.如图是边长为1的3×3的正方形网格,已知△ABC的三个顶点均在正方形格点上,则BC边上的高是( )
A. B. C.2 D.
【分析】先根据勾股定理分别求出AB,AC,BC的长,根据勾股定理逆定理判断出△ABC是直角三角形,再根据三角形的面积公式即可求解.21·cn·jy·com
【解答】解:∵AB,
AC,
BC,
∴AB2+AC2=BC2=10,
∴△ABC是直角三角形,
设BC边上的高为h,
则S,
∴h,
即BC边上的高是,
故选:A.
【点评】本题考查了勾股定理以及勾股定理逆定理,三角形的面积公式,判断出△ABC是直角三角形是解题的关键.2·1·c·n·j·y
4.如图,在△ABC中,∠ACB=90°,点D在AC边上且AD=BD,M是BD的中点,若AC=16,BC=8,则CM等于( )
A.5 B.6 C.8 D.10
【分析】根据勾股定理得出BD,进而利用直角三角形的性质解答即可.
【解答】解:设BD=x,则CD=AC﹣AD=AC﹣BD=16﹣x,
在Rt△BCD中,由勾股定理得:BD2=BC2+CD2,
即:x2=82+(16﹣x)2,
解得:x=10,
∴BD=10,
∵M是BD的中点,
∴CM=5,
故选:A.
【点评】此题考查勾股定理,关键是根据勾股定理得出BD解答.
5.如图,在同一水平线上有相距8m的两棵树AB和CD,其中树AB高8m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )【来源:21cnj*y.co*m】
A.6m B.5m C.4m D.3m
【分析】根据题意表示出AE=4m,设AF=xm,则EF=(8﹣x) m,再利用勾股定理得出答案.
【解答】解:如图所示:根据题意可得,AE=4m,设AF=xm,则EF=(8﹣x) m,
在Rt△AEF中,
AF2+AE2=EF2,
即x2+42=(8﹣x)2,
解得:x=3,
树的折断点离地面的高度是3m.
故选:D.
【点评】此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.
6.如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,E是BD的中点,BD=8,则△AEC的面积为( )
A. B.16 C.8 D.
【分析】由直角三角形斜边上中线的性质可求E=CE=4,利用三角形外角的性质结合等腰三角形的性质可求解∠AEC=90°,再利用三角形的面积公式计算可求解.
【解答】解:∵∠BAD=∠BCD=90°,E是BD的中点,BD=8,
∴AE=CEBD=4,
∴∠ABE=∠BAE,∠CBE=∠BCE,
∵∠AED=∠ABE+∠BAE=2∠ABE,∠CED=∠CBE+∠BCE=2∠CBE,
∴∠AEC=2∠ABE+2∠CBE=2∠ABC,
∵∠ABC=45°,
∴∠AEC=90°,
∴S△ACEAE CE4÷4=8.
故选:C.
【点评】本题主要考查三角形斜边上的中线的性质,三角形外交的性质,三角形的面积,求解AE,CE的长及∠AEC=90°可求解△ACB的面积.
7.如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= 6 .
【分析】设BC=x,AF可用含x的式子表示,CF可以根据勾股定理求出,然后用x表示出BF,在Rt△ABF中,利用勾股定理,可建立关于x的方程,即可得出BF的长.
【解答】解:由折叠的性质知:AD=AF,DE=EF=8﹣3=5;
在Rt△CEF中,EF=DE=5,CE=3,由勾股定理可得:CF=4,
若设AD=AF=x,则BC=x,BF=x﹣4;
在Rt△ABF中,由勾股定理可得:
82+(x﹣4)2=x2,解得x=10,
故BF=x﹣4=6.
故答案为:6.
【点评】考查了勾股定理的应用,综合能力要求较高.同时也考查了列方程求解的能力.
8.如图,AB=BC且AB⊥BC,点P为线段BC上一点,PA⊥PD且PA=PD,若∠A=26°,则∠D的度数为 19° .
【分析】如图,作DH⊥BC交BC的延长线于H.只要证明△ABP≌△PHD(AAS),得出AB=PH,PB=DH,∠A=∠DPH=26°,由AB=CB,推出BC=PH,推出PB=CH=DH,可得∠DCH=45°即可解决问题.
【解答】解:如图,作DH⊥BC交BC的延长线于H.
∵AB⊥BC,DH⊥BC,PA⊥PD,
∴∠B=∠APD=∠H=90°,
∴∠A+∠APB=90°,∠APB+∠DPH=90°,
∴∠A=∠DPH,
∵PA=PD.
∴△ABP≌△PHD(AAS),
∴AB=PH,PB=DH,∠A=∠DPH=26°,
∵AB=CB,
∴BC=PH,
∴PB=CH=DH,
∴∠DCH=45°,
∵∠DCH=∠DPC+∠PDC,
∴∠PDC=19°.
故答案为:19°.
【点评】本题考查全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是添加常用辅助线,构造全等三角形解决问题.www.21-cn-jy.com
9.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 2 .21教育名师原创作品
【分析】作辅助线GH过点E,且GH∥AB,构造一线三垂直模型,用EH分别表示出S1和S2的值,列出关于EH的式子,求出EH即可求出CE.
【解答】解:如图,作GH过点E,且GH∥AB,
∵∠HBE+∠HEB=90°,∠HEB+∠GEF=90°,
∴∠HBE=∠GEF,
∵AC为正方形的对角线,
∴CH=EH,
∴HB=GE,
在△HBE和△GEF中,
,
∴△HBE≌△GEF(ASA),
∴GF=EH,
设EH=a,AF=6﹣2a,
,,
∵2S1=3S2,
∴6a=3(a2﹣9a+18),
解得a=2,
∴CE2,
故答案为2.
【点评】本题主要考查正方形的性质和全等三角形的判定,关键是要能作出辅助线GH,构造一线三垂直模型,出现需要判定的全等三角形,将AF用EH表示出来.2-1-c-n-j-y
10.如图,在△ABC中,∠C=90°,∠A=30°,AB=6cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
①当t= 2 秒时,△PBQ为等边三角形;
②当t= 1.5或 秒时,△PBQ为直角三角形.
【分析】(1)由题意得AP=2tcm,BQ=tcm,BP=AB AP=(6 2t)cm,再由等边三角形的性质得到PB=BQ,即6 2t=t,解方程即可;
(2)讨论∠PQB=90°或∠BPQ=90°时,利用PB与BQ之间的关系,建立方程求解即可.
【解答】解:(1)∵∠C=90°,∠A=30°,AB=8cm,
∴∠B=60°,
∴当PB=BQ时,△PBQ是等边三角形,
由题意得AP=2tcm,BQ=tcm,
∴BP=AB AP=(6 2t)cm,
∴6 2t=t,
解得t=2,
∴当t=2时,△PBQ为等边三角形;
故答案为:2.
(2)∵∠C=90°,∠A=30°,
∴∠B=60°,
∴当△PBQ为直角三角形时,只能是∠PQB=90°或∠BPQ=90°,
当∠PQB=90°时,如图,
∴∠BPQ=30°,
∴BQBP,
∵BP=(6 2t)cm,BQ=tcm,
∴t(6 2t),
解得t=1.5;
当∠BPQ=90°时,如图,
∴∠PQB=30°,
∴BQ=2BP,
∴t=2(6 2t),
解得t,
综上所述,当t=1.5或t时△PBQ为直角三角形.
故答案为:1.5或.
【点评】本题主要考查了等边三角形的判定,含30度角的直角三角形的性质、解一元一次方程,解题的关键在于能够熟练掌握含30度角的直角三角形的性质.21教育网
11.如图,△ABC中,AB=AC=5,CD=1,BD⊥AC,则BC的长度为( )
A.3 B.4 C. D.
【分析】先根据勾股定理求出BD,再根据勾股定理求出BC.
【解答】解:∵AC=5,CD=1,
∴AD=5﹣1=4,
在Rt△ABD中,BD3,
在Rt△BCD中,BC,
故选:C.
【点评】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
12.如图所示,在△ABC中,∠ACB=90°,∠BAC=75°,D为AB中点且DE⊥AB,交BC于点E,AC=6cm,则BE等于( )21cnjy.com
A.3cm B.6cm C.9cm D.12cm
【分析】先利用直角三角形的两个锐角互余可得∠B=15°,再利用线段垂直平分线的性质可得EA=EB,从而可得∠B=∠BAE=15°,然后利用三角形的外角性质可得∠AEC=30°,再在Rt△AEC中,利用含30度角的直角三角形可求出AE的长,即可解答.【来源:21·世纪·教育·网】
【解答】解:∵∠ACB=90°,∠BAC=75°,
∴∠B=90°﹣∠BAC=15°,
∵D为AB中点且DE⊥AB,
∴DE是AB的垂直平分线,
∴EA=EB,
∴∠B=∠BAE=15°,
∴∠AEC=∠B+∠BAE=30°,
∵AC=6cm,
∴AE=2AC=12(cm),
∴BE=AE=12cm,
故选:D.
【点评】本题考查了含30度角的直角三角形,线段垂直平分线的性质,熟练掌握含30度角的直角三角形,以及线段垂直平分线的性质是解题的关键.
13.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若CD=3,BD=4,则BE的长为( )
A.5 B. C. D.2
【分析】利用角平分线的性质得DE=CD=3,再利用勾股定理求出BE即可.
【解答】解:∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DE=CD=3,
∵BD=4,
∴BE,
故选:B.
【点评】本题主要考查了角平分线的性质,勾股定理等知识,熟练掌握角平分线的性质和勾股定理是解题的关键.
14.如图,在△ABC中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
A.4 B. C. D.5
【分析】过A作AE⊥BC于点E,根据勾股定理计算出底边上的高AE的长,然后计算三角形的面积,再以AC为底,利用三角形的面积计算出AC边上的高BD即可.【出处:21教育名师】
【解答】解:过A作AE⊥BC于点E,
∵AB=AC,
∴△ABC是等腰三角形,
∵AE⊥BC,
∴EB=ECCB=3,
在Rt△ABE中,AE4,
∴S△ABC AC BD BC AE6×4=12,
∴5×BD=12,
解得BD.
故选:C.
【点评】此题主要考查了勾股定理的应用,以及等腰三角形的性质,关键是掌握等腰三角形底边上的高和中线重合.
15.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知∠A=90°,正方形ADOF的边长是2,CF=6,则BD的长为( )
A.6 B.2 C.4 D.8
【分析】设BD=x,正方形ADOF的边长为2,则AD=AF=2,根据全等三角形的性质得到CF=CE,BE=BD,根据勾股定理即可得到结论.
【解答】解:正方形ADOF的边长为2,则AD=AF=2,
设BD=x,
∵△BDO≌△BEO,△CEO≌△CFO,
∴BD=BE,CF=CE,
∴AB=x+2,AC=6+2=8,BC=x+6,
∵AC2+AB2=BC2,
∴(x+2)2+82=(x+6)2,
∴x=4,
∴BD=4,
故选:C.
【点评】本题考查了勾股定理,全等三角形的性质,正方形的性质,熟练掌握勾股定理是解题的关键.
16.如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为 32 度.21·世纪*教育网
【分析】根据已知条件得到点A,B,C,D在以E为圆心,AC为直径的同一个圆上,根据圆周角定理得到∠DEB=116°,根据直角三角形的性质得到DE=BEAC,根据等腰三角形的性质即可得到结论.
【解答】解:∵∠ABC=∠ADC=90°,
∴点A,B,C,D在以E为圆心,AC为直径的同一个圆上,
∵∠BAD=58°,
∴∠DEB=116°,
∵DE=BEAC,
∴∠EBD=∠EDB=32°,
故答案为:32.
【点评】本题考查了直角三角形斜边上的中线的性质,圆周角定理,推出A,B,C,D四点共圆是解题的关键.
17.如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM= 3 .
【分析】过点C作CF⊥AB于点F,由旋转的性质可得AD=AC,BE=BC,利用“一线三等角“证得∠D=∠CAF,从而可判定△DAM≌△ACF(AAS),则DM=AF.同理可证,△BFC≌△ENB(AAS),则BF=EN=2,再由AB=5,可得AF,即DM的值.
【解答】解:过点C作CF⊥AB于点F,如图所示:
∵旋转,
∴AD=AC,BE=BC,
∵DM⊥AB于点M,EN⊥AB于点N,CF⊥AB于点F,
∴∠AMD=∠AFC=∠BFC=∠BNE=90°,
∴∠D+∠DAM=90°,
∵∠CAD=90°,
∴∠CAF+∠DAM=90°,
∴∠D=∠CAF,
∴在△DAM和△ACF中,
,
∴△DAM≌△ACF(AAS),
∴DM=AF.
同理可证,△BFC≌△ENB(AAS),
∴BF=EN=2,
∵AB=5,
∴AF=3,
∴DM=3.
故答案为:3.
【点评】本题考查了旋转的性质、全等三角形的判定与性质等知识点,正确作出辅助线构造全等三角形是解题的关键.
18.如图,在矩形ABCD中,AB=6,BC=18,把矩形折叠,使点D与点B重合,点C落在点E处,则折痕FG的长为 2 .
【分析】连接BD,在Rt△ABD中,求得BD的长,在Rt△ADF中运用勾股定理求得DF的长,即可得到DF长,最后在Rt△DOF中求得FO的长,即可得到答案.
【解答】解:如图,连接BD,交FG于O,则由轴对称的性质可知,FG垂直平分BD,
Rt△ABD中,BD,
由折叠可得DOBD=3,∠BFO=∠DFO,
由AB∥CD可得,∠DFO=∠BGO,
∴∠DFO=∠BGO,
∴BF=BG,即△BFG是等腰三角形,
∴BD平分FG,
∴OF=OG,
由折叠知,BF=DF,
设BF=DF=x,则AF=18﹣x,
在Rt△ABF中,(18﹣x)2+62=x2,
解得x=10,即DF=10,
∴Rt△DOF中,OF,
∴FG=2FO=2.
故答案为:2.
【点评】本题是折叠问题,主要考查了折叠的性质,勾股定理以及矩形的性质的综合应用,解决问题的关键是根据勾股定理列方程求解.21世纪教育网版权所有
19.将一等腰直角的三角板△ABC如图放置在平面直角坐标系中,若∠ABC=90°.
(1)若如图①放置时,已知点A(0,﹣4),B(1,0),求点C的坐标;
(2)若如图②放置时,已知点A(0,0),B(3,1),求点C的坐标.
【分析】(1)过点C作x轴的垂线,交x轴于点D,再利用边角关系证明∴△BCD≌△ABO,求出CD=1,OD=3,即可得出答案;21*cnjy*com
(2)过B作x轴的垂线,交x轴于点D,过点C作DB的垂线交DB的延长线于点E,再利用边角关系证明△ABD≌△BCE,求出CE=1,DE=4,即可得出答案.
【解答】解:(1)过点C作x轴的垂线,交x轴于点D,
∵A(0,﹣4),B(1,0),
∴OA=4,OB=1,
∴∠ABC=90°,∠AOB=90°,
∴∠CBD+∠OBA=90°,∠OAB+∠OBA=90°,
∴∠CBD=∠BAO,
∵AB=BC,∠AOB=∠BDC=90°,
∴△BCD≌△ABO(AAS),
∴CD=BO=1,BD=AO=4,
∴OD=3,
∴点C坐标为(﹣3,1);
(2)过B作x轴的垂线,交x轴于点D,过点C作DB的垂线交DB的延长线于点E,
∵A(0,0),B(3,1),
∴OD=3,BD=1,
∵∠ABC=90°,∠ADB=90°,
∴∠CBE+∠OBD=90°,∠BAD+∠OBD=90°,
∴∠BAD=∠CBE,
∵AB=BC,∠ADB=∠BEC=90°,
∴△ABD≌△BCE(AAS),
∴CE=BD=1,BE=AD=3,
∴DE=4,
∴点C的横坐标为3﹣1=2,
∴点C坐标为(2,4).
【点评】本题考查全等三角形的判定与性质以及坐标与图形性质,利用全等三角形的判定定理证出三角形全等是解题关键.
20.如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.
(1)当t为何值时,△PAB是等腰三角形;
(2)当t为何值时,△PAB是直角三角形.
【分析】(1)先由勾股定理求出BC=4,再分三种情况进行讨论:①若BA=BP;②若AB=AP;③若PA=PB.分别列出方程求解即可;
(2)先由勾股定理求出,再分两种情况进行讨论:①当∠APB=90°时,点P与点C重合,则t=6;②当∠BAP=90°时,根据勾股定理列方程,求解即可.
【解答】解:(1)在Rt△ABC中,AB=5,AC=3,
由勾股定理可得BC=4.
由题意可得MP=t.
当△PAB是等腰三角形时,分三种情况:
①若BA=BP,如图1.
则有|10﹣t|=5,
解得t=5或15;
②若AB=AP,如图2.
则有PB=2BC,故有10﹣t=8,
解得t=2;
③若PA=PB,如图3.
则有,
解得.
综上,当t为5或15或2或时,△PAB是等腰三角形.
(2)由MP=t,BP=|10﹣t|,由勾股定理可得.
当△PAB是直角三角形时,分两种情况:
①当∠APB=90°时,如图4.
点P与点C重合,则t=6;
②当∠BAP=90°时,如图5.
则有,解得.
综上,当t为6或时,△PAB是直角三角形.
【点评】本题考查了勾股定理,等腰三角形的判定与性质,进行分类讨论是解题的关键.
声明:试题解析著作权属21世纪教育网所有,未经书面同意,不得复制发布日期:2023/1/24 21:29:03;用户:陈梦洁;邮箱:17858502426;学号:28029722
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
