2.4 概率的简单应用

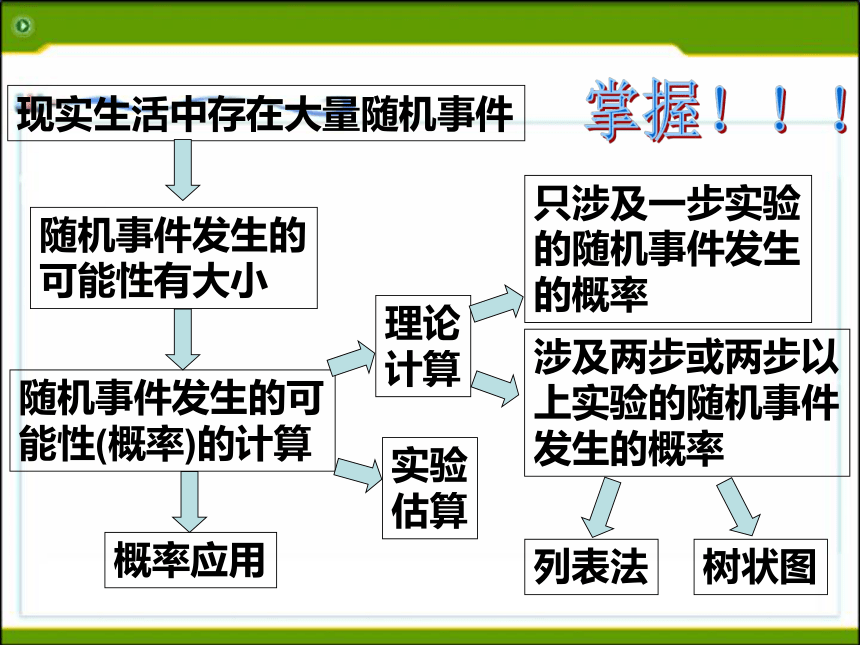
课件24张PPT。新浙教版数学九年级（上）2.4 概率的简单应用现实生活中存在大量随机事件随机事件发生的
可能性有大小随机事件发生的可
能性(概率)的计算理论
计算实验
估算只涉及一步实验
的随机事件发生
的概率涉及两步或两步以
上实验的随机事件
发生的概率列表法树状图概率应用掌握！！！请小组内讨论下面问题：1.如果有人买了彩票，一定希望知道中奖的概率有多大．那么怎么样来估计中奖的概率呢？2.出门旅行的人希望知道乘坐哪一种交通工具发生事故的可能性较小？概率与人们生活密切相关，在生活，生产和科研等各个领域都有着广泛的应用．由上面两个问题，你能得到什么？某商场举办有奖销售活动，每张奖券获奖的可能性相同，以每10000张奖券为一个开奖单位，设特等奖１个，一等奖10个，二等奖100个，问１张奖券中一等奖的概率是多少？中奖的概率是多少？解:中一等奖的概率是P=中奖的概率是P=进一步了解1.什么叫概率？事件发生的可能性的大小叫这一事件发生的概率2.概率的计算公式：若事件发生的所有可能结果总数为n，事件Ａ发生的可能结果数为m，则Ｐ（Ａ）＝3.估计概率 在实际生活中，我们常用频率来估计概率，在大量重复的实验中发现频率接近于哪个数，把这个数作为概率．温故而知新初步尝试共同探索：1.某商场举办有奖销售活动，每张奖券获奖的可能性相同，以每10000张奖券为一个开奖单位，设特等奖１个，一等奖10个，二等奖100个，问１张奖券中一等奖的概率是多少？中奖的概率是多少？解:因为10000张奖券中能中一等奖的张数是10张,所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张),
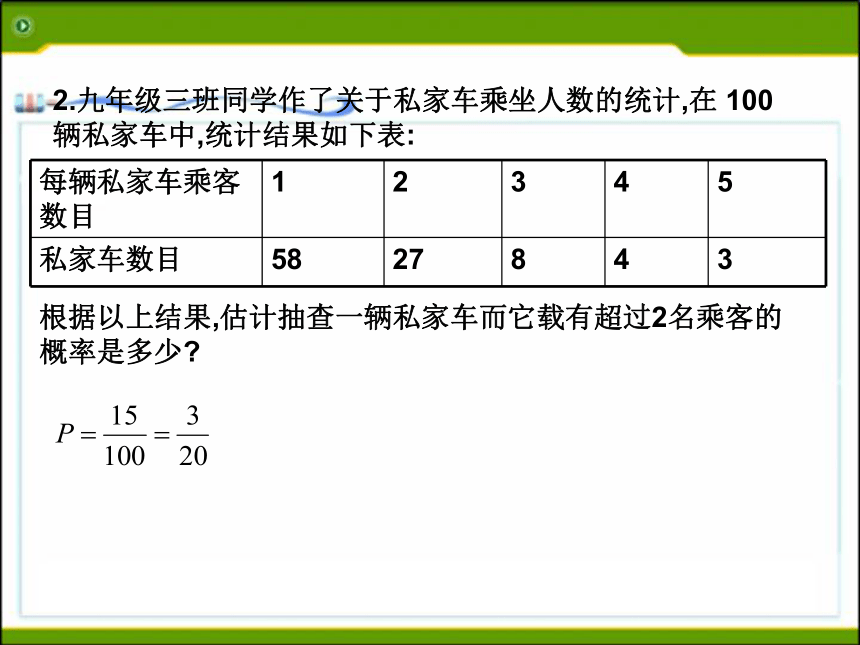
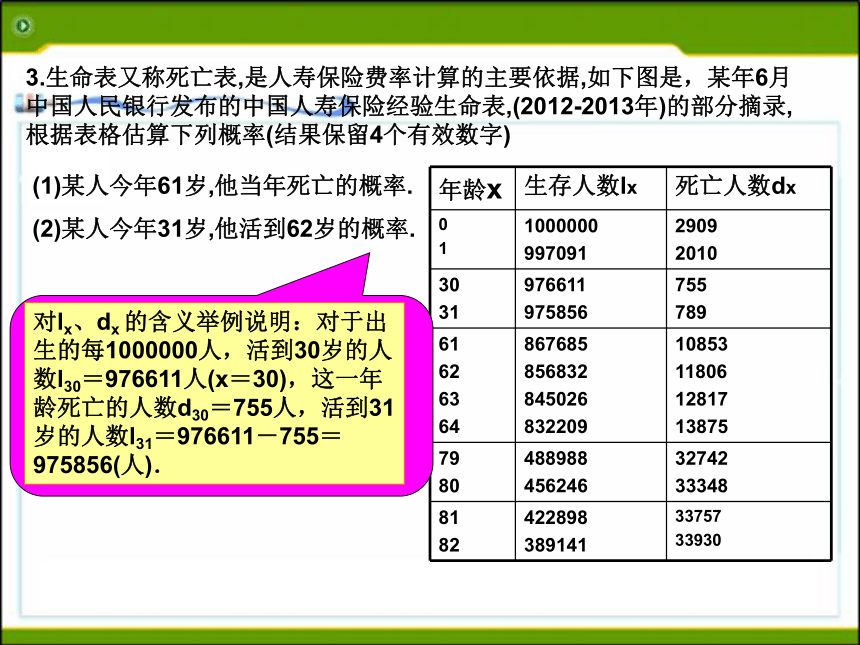
所以1张奖券中奖的概率是2.九年级三班同学作了关于私家车乘坐人数的统计,在 100辆私家车中,统计结果如下表:根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少?3.生命表又称死亡表,是人寿保险费率计算的主要依据,如下图是，某年6月中国人民银行发布的中国人寿保险经验生命表,(2012-2013年)的部分摘录,根据表格估算下列概率(结果保留4个有效数字)(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.解(1)由表知,61岁的生存人数l61=867685,61岁的死亡人数=d6110853,所以所求死亡的概率P=(2)由表知,l31=975856, l62=856832,所以所求的概率:答:他当年死亡的概率约为0.01251,活到62岁的概率约为0.8780.(3)一个80岁的人在当年死亡的概率是多少?
(4)一个61岁的人,他活到82岁的概率是多少?
(5)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元?1.什么叫概率？事件发生的可能性的大小叫这一事件发生的概率2.概率的计算公式：若事件发生的所有可能结果总数为n，事件Ａ发生的可能结果数为m，则Ｐ（Ａ）＝3.估计概率 在实际生活中，我们常用频率来估计概率，在大量重复的实验中发现频率接近于哪个数，把这个数作为概率．温故而知新当堂巩固1.有一组互不全等的三角形，它们的边长均为整数，每个三角形有两条边的长分别为5和7．
（1）请写出其中一个三角形的第三边的长；
（2）设组中最多有n个三角形，求n的值；
（3）当这组三角形个数最多时，从中任取一个，求该三角形周长为偶数的概率．解：（1）设三角形的第三边为x，
∵每个三角形有两条边的长分别为5和7，
∴7﹣5＜x＜5+7，∴2＜x＜12，
∴其中一个三角形的第三边的长可以为10．（2）∵2＜x＜12，它们的边长均为整数，
∴x=3，4，5，6，7，8，9，10，11，
∴组中最多有9个三角形，∴n=9；（3）∵当x=4，6，8，10时，该三角形周长为偶数，
∴该三角形周长为偶数的概率是2.已知甲同学手中藏有三张分别标有数字 ， ，1的卡片，
乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同.现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为a，b.
（1）请你用树形图或列表法列出所有可能的结果.
（2）现制定这样一个游戏规则：若所选出的a，b能使得
有两个不相等的实数根，则甲获胜；否则乙获胜.请问这样的游戏规则公平吗？请你用概率知识解释。甲1乙132∴(a,b)取值结果共有9种
（2）∵Δ=b2－4a与对应（1）中的结果为：－1、2、7、0、3、8、－3、0、5 ∴P(甲获胜)= P(Δ＞0)=
＞P(乙获胜) ＝ 不公平3.小明和小刚玩“石头、剪刀、布”的游戏，每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种，规定“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”，相同的手势是和局．（1）用树形图或列表法计算在一局游戏中两人获胜的概率各是多少？（2）如果两人约定：只要谁率先胜两局，就成了游戏的赢家．用树形图或列表法求只进行两局游戏便能确定赢家的概率．解：（1）画树状图得：∵总共有9种情况，每一种出现的机会均等，每人获胜的情形都是3种，
∴两人获胜的概率都是4.小明和小刚玩“石头、剪刀、布”的游戏，每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种，规定“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”，相同的手势是和局．（1）用树形图或列表法计算在一局游戏中两人获胜的概率各是多少？（2）如果两人约定：只要谁率先胜两局，就成了游戏的赢家．用树形图或列表法求只进行两局游戏便能确定赢家的概率．（2）由（1）可知，一局游戏每人胜、负、和的机会均等，都为
任选其中一人的情形可画树状图得：∵总共有9种情况，每一种出现的机会均等，当出现（胜，胜）或（负，负）这两种情形时，赢家产生，∴两局游戏能确定赢家的概率为：自我挑战1.连掷两枚骰子,它们的点数相同的
概率是______.2 .转动如图所示的转盘两次,两次所得的颜色相同的概率是______.3 .某口袋里放有编号为1~6的6个球,先从中摸出一个,将它放回口袋中后,再摸一次,两次摸到的球相同的概率是_____.4 . 利用计算器产生1~6的随机数(整数)连续两次随机数相同的概率是______.5.一口袋里装有若干个红球,为了估计红球的数目,从中取出10只红球做上记号后放回,充分搅和均匀后,每次从中取出10只,统计有记号的红球后放回,再搅和均匀,这样反复做了10次,得到的有记号的红球数目如下:3，2，2，4，1，3，2，0，1，3，据此可推算口袋中原有红球约_____只.(四舍五入到个位)486.连掷两枚骰子,点数和等于4的概率是( )
A. B. C. D.A7. 一个密码锁由三个数字组成,每个数字都是0~9这十个数字中的一个,只有当三个数字与设定的密码相同时,才能将锁打开,小明只记得头一个数字,则他一次就能打开该锁的概率是( )
A. B. C. D.DD8. 抽屉里有尺码相同的3双黑袜子和2双白袜子,分散混放在一起,在夜晚不开灯的情况下,随意拿出2只,“它们恰好是一双”的概率是( )
A. B. C. D.C9. 有两个信封,每个信封内都装有写上数1、2、3的卡片,现从这两个信封中各任意抽出一张卡片,两张卡片上的数的和不大于3的概率是( )
A. B. C. D.甲：无论如何总是上开来的第一辆车，
乙：先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况，如果第二辆车的舒适程度比第一辆好，他就上第二辆车；如果第二辆车不比第一辆好，他就上第三辆车。假设每天某一时段开往温州有三辆专车（票价相同），有两人相约来温州游玩，但是他们不知道这些车的舒适程度，也不知道专车开过来的顺序，两人采用了不同的乘车方案： 如果把这三辆车的舒适程度分为上、中、下三等，请尝试着解决下面的问题：（2）你认为甲、乙采用的方案，哪一种方案使自己乘上等车的可能性大？为什么？（1）三辆车按出现的先后顺序共有哪几种不同的可能？拓展练习谢谢大家！