1.1锐角三角函数(1)导学案
图片预览

文档简介
1.1 锐角三角函数
一、学习目标:
1、经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念。
2、掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数。
3、掌握在直角三角形中,锐角三角函数与边之间的关系。
4、了解锐角三角函数值都是正实数,会根据锐角三角函数的定义求锐角三角函数值。
重点:锐角的正弦、余弦、正切和锐角三角函数的概念。
难点:锐角三角函数的意义和以角为自变量,都与一次函数和二次函数有很大区别,概念比较抽象,所以理解上有较大难度。
二、课前预习,课中交流展示:
函数的概念:一般地,在某个变化过程中,设 ( http: / / www.21cnjy.com )有两个变量x,y,如果对于x的每一个确定的值,y都有唯一确定的值,那么就说y是x的函数,x叫做自变量。
1、(1)如图:若∠A=30°,在角的边上取一点B,作BC⊥AC,量得BC=1。
计算: ;= ;= .
若∠A=30°,在角的边上取一点B,作BC⊥AC,量得BC=2。
计算: ;= ;= .
若∠A=30°,在角的边上任取一点B,量得BC=a, 计算: ;= ;= .
通过上面的操作:当∠A的度数确定为30°时,比值,,都是一个确定的值。
(2)如图:若∠A=45°,在角的边上取一点B,作BC⊥AC,量得BC=1。
计算: ;= ;= .
若∠A=45°,在角的边上取一点B,作BC⊥AC,量得BC=2。
计算: ;= ;= .
若∠A=45°,在角的边上任取一点B,量得BC=a ,计算: ;= ;= .
通过上面的操作,当∠A的读数确定为45°时,比值,,都是一个确定的值。
(3)如图,B,是一边上的任意两点,作BC⊥AC于点C,于点C。
证明:比值,,.
3、请同学们仔细预习书本第5页的概念,完成下列填空。
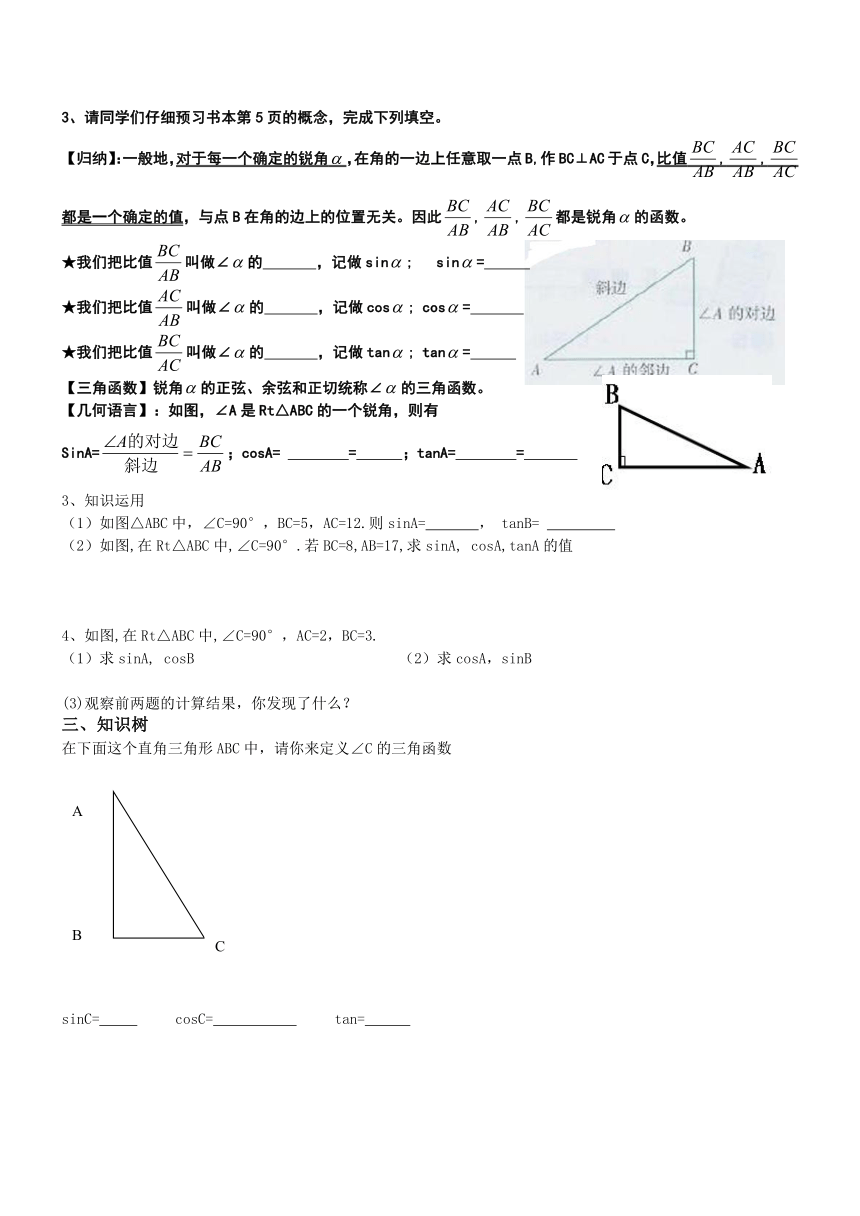
【归纳】:一般地,对于每一个确定的锐角,在角的一边上任意取一点B,作BC⊥AC于点C,比值,,都是一个确定的值,与点B在角的边上的位置无关。因此,,都是锐角的函数。
★我们把比值叫做∠的 ,记做sin; sin=
★我们把比值叫做∠的 ,记做cos; cos=
★我们把比值叫做∠的 ,记做tan; tan=
【三角函数】锐角的正弦、余弦和正切统称∠的三角函数。
【几何语言】:如图,∠A是Rt△ABC的一个锐角,则有
SinA=;cosA= = ;tanA= =
3、知识运用
(1)如图△ABC中,∠C=90°,BC=5,AC=12.则sinA= , tanB=
(2)如图,在Rt△ABC中,∠C=90°.若BC=8,AB=17,求sinA, cosA,tanA的值
4、如图,在Rt△ABC中,∠C=90°,AC=2,BC=3.
(1)求sinA, cosB (2)求cosA,sinB
(3)观察前两题的计算结果,你发现了什么?
三、知识树
在下面这个直角三角形ABC中,请你来定义∠C的三角函数
sinC= cosC= tan=
教与学反思:
四、课堂检测:
在Rt△ABC中,∠C=90°,AC=6, BC=8,那么sinA= cosA =
tanB = .
已知sinA =,则cosA= ,tanA= .
在Rt△ABC中,∠C=90°,BC=6cm,sinA=, 则AC的长是 cm.
如图,小丽沿着倾斜角为β的山坡从A点前进a米到达B点,则山坡AB的水平距离AC等于( )米.
A. a sinβ B. a cosβ C. a D.
5. 在Rt△ABC中,∠C=90 ( http: / / www.21cnjy.com )°,各边的长度都扩大3倍,则锐角A的三角函数值( ) A. 扩大3倍 B. 缩小3倍 C. 不变 D. 不能确定
6. 如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
第8题 第9题 第10题
7. 如图,在等腰梯形ABCD中,AD∥BC,AC⊥AB,cosB= ,BC=26.
求:⑴ cos∠DAC的值 .⑵ AD的长.
A
C
B
A
B
C
β
a
C
A
D
B
C
·
B
A
O
D
小贴士: 当求一个角的三角函数值不明显时,能否可以将其转化成求与之相等角的三角函数值?
一、学习目标:
1、经历锐角的正弦、余弦和正切的探索过程,了解三角函数的概念。
2、掌握正弦、余弦和正切的符号,会用符号表示一个锐角的三角函数。
3、掌握在直角三角形中,锐角三角函数与边之间的关系。
4、了解锐角三角函数值都是正实数,会根据锐角三角函数的定义求锐角三角函数值。
重点:锐角的正弦、余弦、正切和锐角三角函数的概念。
难点:锐角三角函数的意义和以角为自变量,都与一次函数和二次函数有很大区别,概念比较抽象,所以理解上有较大难度。
二、课前预习,课中交流展示:
函数的概念:一般地,在某个变化过程中,设 ( http: / / www.21cnjy.com )有两个变量x,y,如果对于x的每一个确定的值,y都有唯一确定的值,那么就说y是x的函数,x叫做自变量。
1、(1)如图:若∠A=30°,在角的边上取一点B,作BC⊥AC,量得BC=1。
计算: ;= ;= .
若∠A=30°,在角的边上取一点B,作BC⊥AC,量得BC=2。
计算: ;= ;= .
若∠A=30°,在角的边上任取一点B,量得BC=a, 计算: ;= ;= .
通过上面的操作:当∠A的度数确定为30°时,比值,,都是一个确定的值。
(2)如图:若∠A=45°,在角的边上取一点B,作BC⊥AC,量得BC=1。
计算: ;= ;= .
若∠A=45°,在角的边上取一点B,作BC⊥AC,量得BC=2。
计算: ;= ;= .
若∠A=45°,在角的边上任取一点B,量得BC=a ,计算: ;= ;= .
通过上面的操作,当∠A的读数确定为45°时,比值,,都是一个确定的值。
(3)如图,B,是一边上的任意两点,作BC⊥AC于点C,于点C。
证明:比值,,.
3、请同学们仔细预习书本第5页的概念,完成下列填空。
【归纳】:一般地,对于每一个确定的锐角,在角的一边上任意取一点B,作BC⊥AC于点C,比值,,都是一个确定的值,与点B在角的边上的位置无关。因此,,都是锐角的函数。
★我们把比值叫做∠的 ,记做sin; sin=
★我们把比值叫做∠的 ,记做cos; cos=
★我们把比值叫做∠的 ,记做tan; tan=
【三角函数】锐角的正弦、余弦和正切统称∠的三角函数。
【几何语言】:如图,∠A是Rt△ABC的一个锐角,则有
SinA=;cosA= = ;tanA= =
3、知识运用
(1)如图△ABC中,∠C=90°,BC=5,AC=12.则sinA= , tanB=
(2)如图,在Rt△ABC中,∠C=90°.若BC=8,AB=17,求sinA, cosA,tanA的值
4、如图,在Rt△ABC中,∠C=90°,AC=2,BC=3.
(1)求sinA, cosB (2)求cosA,sinB
(3)观察前两题的计算结果,你发现了什么?
三、知识树
在下面这个直角三角形ABC中,请你来定义∠C的三角函数
sinC= cosC= tan=
教与学反思:
四、课堂检测:
在Rt△ABC中,∠C=90°,AC=6, BC=8,那么sinA= cosA =
tanB = .
已知sinA =,则cosA= ,tanA= .
在Rt△ABC中,∠C=90°,BC=6cm,sinA=, 则AC的长是 cm.
如图,小丽沿着倾斜角为β的山坡从A点前进a米到达B点,则山坡AB的水平距离AC等于( )米.
A. a sinβ B. a cosβ C. a D.
5. 在Rt△ABC中,∠C=90 ( http: / / www.21cnjy.com )°,各边的长度都扩大3倍,则锐角A的三角函数值( ) A. 扩大3倍 B. 缩小3倍 C. 不变 D. 不能确定
6. 如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,BC=3.则sin∠BAC= ;sin∠ADC= .
第8题 第9题 第10题
7. 如图,在等腰梯形ABCD中,AD∥BC,AC⊥AB,cosB= ,BC=26.
求:⑴ cos∠DAC的值 .⑵ AD的长.
A
C
B
A
B
C
β
a
C
A
D
B
C
·
B
A
O
D
小贴士: 当求一个角的三角函数值不明显时,能否可以将其转化成求与之相等角的三角函数值?
