浙教版数学七年级上册 5.4.3调配问题与工程问题 课件(共26张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 5.4.3调配问题与工程问题 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 497.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第5章 一元一次方程
5.4 一元一次方程的应用
第3课时 调配问题与工程问题
教学目标
1.进一步体验方程是刻画现实世界的有效的数学模型.
2.掌握调配问题、工程问题的基本数量关系,进一步掌握分析数量关系、列方程的方法.
3.会用列表法、图示法分析应用题中的数量关系.
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
分析 : 设应调往甲处x人,题目中涉及的有关数量及其关系能用表格去表示吗?
情境导入
一、调配问题
甲 处 乙 处
原有人数
增加人数
增加后人数
23
17
x
20 – x
23+x
17+20-x
等量关系: 甲处增加后人数=2×乙处增加后人数
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
知识讲解
解:设应调往甲处x人,
根据题意,得23+x=2(17+20-x)
解这个方程,得x=17
所以20-x=3
答:应调往甲处17人,乙处3人.
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
方法二:设调往乙处的人数为x
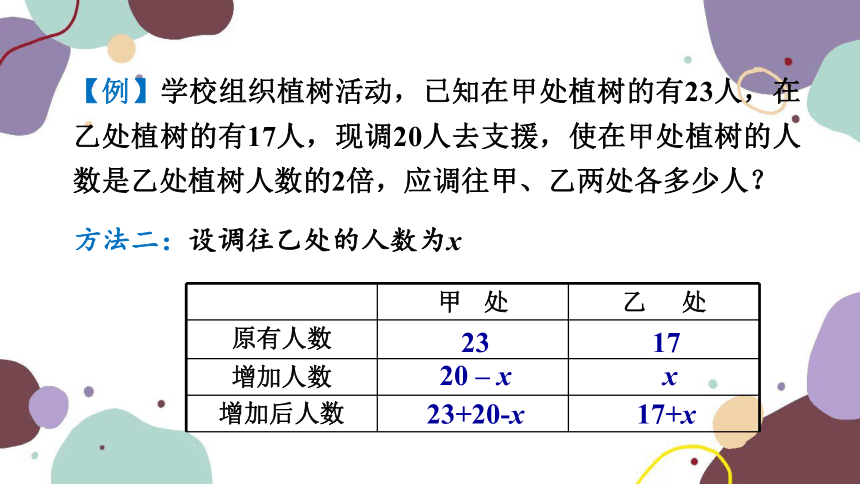
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
甲 处 乙 处
原有人数
增加人数
增加后人数
23
17
x
20 – x
23+20-x
17+x
特别提示:在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.
解:设应调往甲处x人,
根据题意,得23+20-x=2(17+x)
解这个方程,得x=3
所以20-x=17
答:应调往甲处17人,乙处3人.
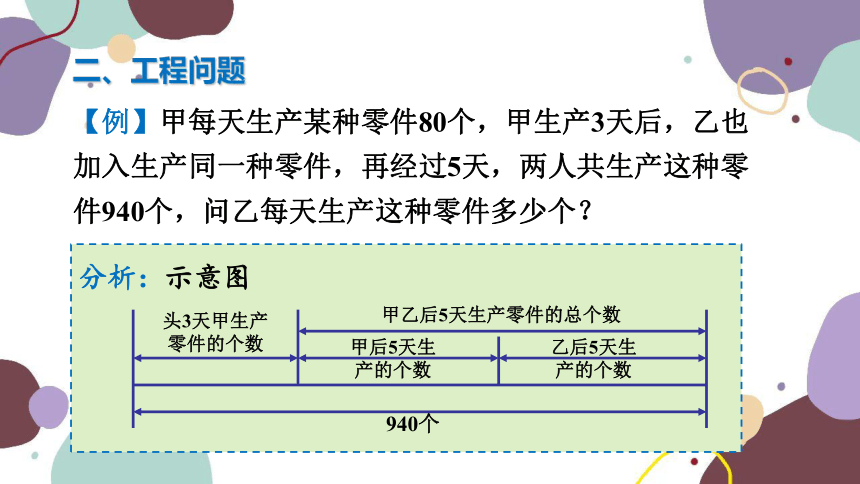
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
二、工程问题
分析:示意图
头3天甲
生产零件
的个数
后5天甲
生产零件
的个数
后5天乙
生产零件
的个数
940
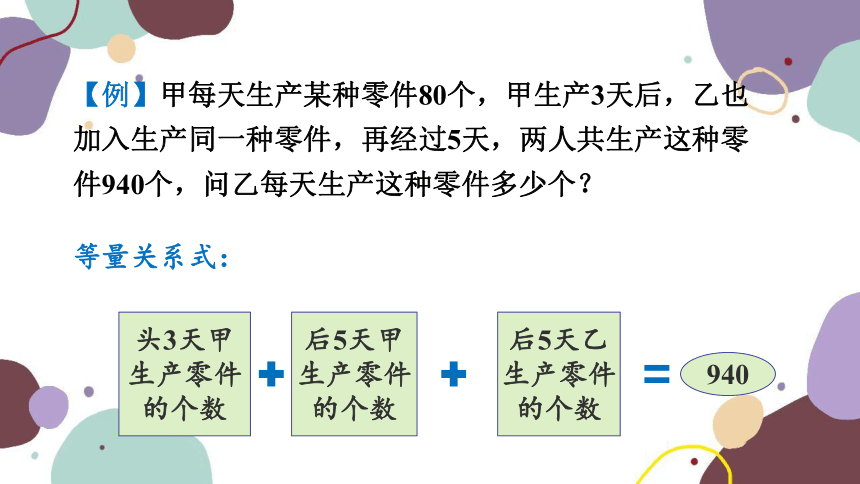
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
等量关系式:
解:设乙每天生产零件的个数为x,
由题意得,3×80+5×80+5 =940
解得x=60
答:乙每天生产零件60个.
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
归纳小结
工程问题
工作量:生产零件的个数,有具体数量.
效率:单位时间内生产零件的个数.
时间:完成工作所用的时间.
工程问题的基本数量关系:工作量=效率×时间.
三、销售问题
分析:
设该商品销售价为x元
毛利率
进价
销售价
5%
400
x
代入
解:设该商品销售价为x元,
由题意,得 ,解得 x=420
因为 ,所以该商品打7折销售.
归纳小结
销售问题
甲队干3天的工作量+乙队干(x+3)天的工作量=1
活学活用
【例1】一个道路工程,甲队单独施工9天完成,乙队单独施工24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
请列出题中的等量关系吗?
甲队干3天的工作量+乙队干(x+3)天的工作量=1
当问题中的工作量无法用具体数值表示时,我们常把完成一项工作的总工作量用1表示,效率就用几分之一表示.
【例2】食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?
活学活用
A种饮料需要的添加剂
B种饮料需要的添加剂
270克
列示意图
【例2】食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?
等量关系:
A种饮料需要的添加剂+B种饮料需要的添加剂=270g
活学活用
解:设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,
由题意得2x+3(100-x)=270,
解得x=30.
所以100-30=70.
答:A饮料生产了30瓶,B饮料生产了70瓶.
A种饮料需要的添加剂+B种饮料需要的添加剂=270g
活学活用
【例3】有一批货物需要从A地运往B地,货主准备租用甲、乙两种货车,已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付50元计算,问货主应付运费多少元?
次数 第一次 第二次
甲种货车辆数 1 5
乙种货车辆数 3 6
合计运货吨数 11.5 35
活学活用
解:设乙种货车每辆每次运x吨,
则甲种货车每辆每次运(11.5-3x)吨,
6x+5×(11.5-3x)=35,
解得x=2.5,
甲种货车:11.5-3x=4(吨),
共运货物:3×4+5×2.5=24.5(吨).
运费:50×24.5=1225(元).
答:货主应付运费1225元.
1、一批零件,甲每小时能加工80个,则甲3小时可加工______个零件, x小时可加工______个零件;加工a个零件,甲需______小时完成.
240
80x
巩固练习
2、一项工程甲独做需6天完成,则甲独做一天可完成这项工程的____;若乙独做比甲快2天完成,则乙独做一天可完成这项工程的______.
3、一件商品的标价为50元,现以八折销售,则售价为 ,若进价为33元,则它的利润为 ;
4、某商品的原价是a元,提价10%后再降价10%,这时这件商品的价格是( )
解析:由题意,得a(1+10%)(1-10%)=0.99a
故答案选C.
40元
7元
C
5、一件商品按成本价提高30%后标价,又以8折销售,售价为208元,这种商品的成本价是多少元?
解:设成本价为x元,
由题意,得80%×(1+30%)x=208
解得 x=200
答:这种商品的成本价是200元.
课堂小结
2.工程问题的基本数量关系:工作量=效率×时间.
1.分析方法:列表法,图示法
谢谢观看
第5章 一元一次方程
5.4 一元一次方程的应用
第3课时 调配问题与工程问题
教学目标
1.进一步体验方程是刻画现实世界的有效的数学模型.
2.掌握调配问题、工程问题的基本数量关系,进一步掌握分析数量关系、列方程的方法.
3.会用列表法、图示法分析应用题中的数量关系.
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
分析 : 设应调往甲处x人,题目中涉及的有关数量及其关系能用表格去表示吗?
情境导入
一、调配问题
甲 处 乙 处
原有人数
增加人数
增加后人数
23
17
x
20 – x
23+x
17+20-x
等量关系: 甲处增加后人数=2×乙处增加后人数
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
知识讲解
解:设应调往甲处x人,
根据题意,得23+x=2(17+20-x)
解这个方程,得x=17
所以20-x=3
答:应调往甲处17人,乙处3人.
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
方法二:设调往乙处的人数为x
【例】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人,现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
甲 处 乙 处
原有人数
增加人数
增加后人数
23
17
x
20 – x
23+20-x
17+x
特别提示:在解决实际问题时,我们一般可以通过分析实际问题, 抽象出数学问题, 然后运用数学思想方法解决问题.用列表分析数量关系是常用的方法.
解:设应调往甲处x人,
根据题意,得23+20-x=2(17+x)
解这个方程,得x=3
所以20-x=17
答:应调往甲处17人,乙处3人.
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
头3天甲生产
零件的个数
甲乙后5天生产零件的总个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
二、工程问题
分析:示意图
头3天甲
生产零件
的个数
后5天甲
生产零件
的个数
后5天乙
生产零件
的个数
940
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
等量关系式:
解:设乙每天生产零件的个数为x,
由题意得,3×80+5×80+5 =940
解得x=60
答:乙每天生产零件60个.
【例】甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
归纳小结
工程问题
工作量:生产零件的个数,有具体数量.
效率:单位时间内生产零件的个数.
时间:完成工作所用的时间.
工程问题的基本数量关系:工作量=效率×时间.
三、销售问题
分析:
设该商品销售价为x元
毛利率
进价
销售价
5%
400
x
代入
解:设该商品销售价为x元,
由题意,得 ,解得 x=420
因为 ,所以该商品打7折销售.
归纳小结
销售问题
甲队干3天的工作量+乙队干(x+3)天的工作量=1
活学活用
【例1】一个道路工程,甲队单独施工9天完成,乙队单独施工24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
请列出题中的等量关系吗?
甲队干3天的工作量+乙队干(x+3)天的工作量=1
当问题中的工作量无法用具体数值表示时,我们常把完成一项工作的总工作量用1表示,效率就用几分之一表示.
【例2】食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?
活学活用
A种饮料需要的添加剂
B种饮料需要的添加剂
270克
列示意图
【例2】食品安全是关乎民生的问题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?
等量关系:
A种饮料需要的添加剂+B种饮料需要的添加剂=270g
活学活用
解:设A饮料生产了x瓶,则B饮料生产了(100-x)瓶,
由题意得2x+3(100-x)=270,
解得x=30.
所以100-30=70.
答:A饮料生产了30瓶,B饮料生产了70瓶.
A种饮料需要的添加剂+B种饮料需要的添加剂=270g
活学活用
【例3】有一批货物需要从A地运往B地,货主准备租用甲、乙两种货车,已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付50元计算,问货主应付运费多少元?
次数 第一次 第二次
甲种货车辆数 1 5
乙种货车辆数 3 6
合计运货吨数 11.5 35
活学活用
解:设乙种货车每辆每次运x吨,
则甲种货车每辆每次运(11.5-3x)吨,
6x+5×(11.5-3x)=35,
解得x=2.5,
甲种货车:11.5-3x=4(吨),
共运货物:3×4+5×2.5=24.5(吨).
运费:50×24.5=1225(元).
答:货主应付运费1225元.
1、一批零件,甲每小时能加工80个,则甲3小时可加工______个零件, x小时可加工______个零件;加工a个零件,甲需______小时完成.
240
80x
巩固练习
2、一项工程甲独做需6天完成,则甲独做一天可完成这项工程的____;若乙独做比甲快2天完成,则乙独做一天可完成这项工程的______.
3、一件商品的标价为50元,现以八折销售,则售价为 ,若进价为33元,则它的利润为 ;
4、某商品的原价是a元,提价10%后再降价10%,这时这件商品的价格是( )
解析:由题意,得a(1+10%)(1-10%)=0.99a
故答案选C.
40元
7元
C
5、一件商品按成本价提高30%后标价,又以8折销售,售价为208元,这种商品的成本价是多少元?
解:设成本价为x元,
由题意,得80%×(1+30%)x=208
解得 x=200
答:这种商品的成本价是200元.
课堂小结
2.工程问题的基本数量关系:工作量=效率×时间.
1.分析方法:列表法,图示法
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
