浙教版八年级上册 2.1 图形的轴对称 课件(21张PPT)
文档属性
| 名称 | 浙教版八年级上册 2.1 图形的轴对称 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
2.1 图形的轴对称
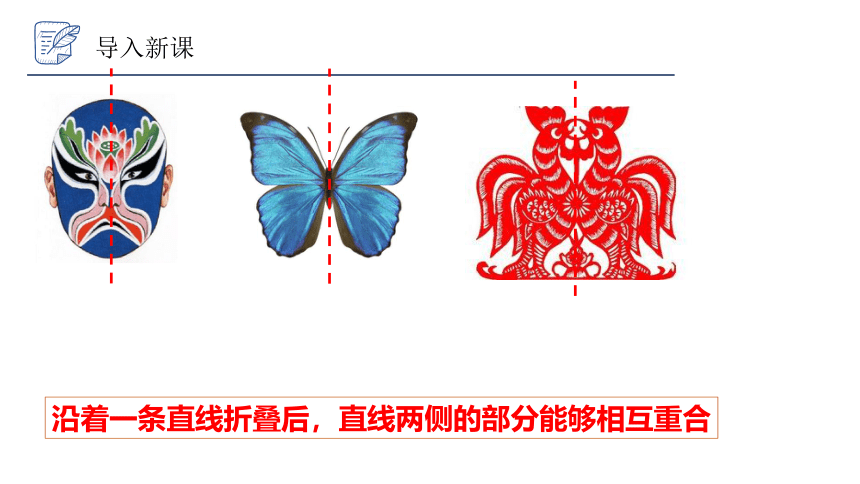
沿着一条直线折叠后,直线两侧的部分能够相互重合
导入新课
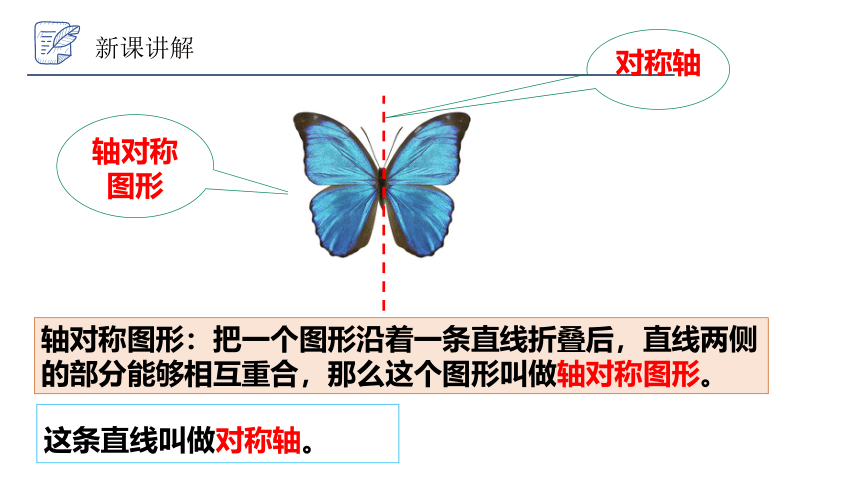
这条直线叫做对称轴。
轴对称图形
新课讲解
对称轴
轴对称图形:把一个图形沿着一条直线折叠后,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形。
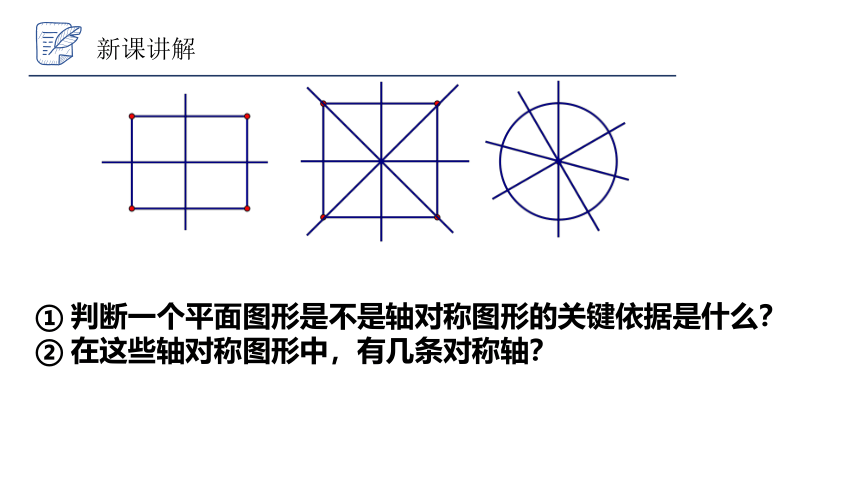
新课讲解
① 判断一个平面图形是不是轴对称图形的关键依据是什么?
② 在这些轴对称图形中,有几条对称轴?
1.下列图形是轴对称图形吗?你是怎么判别的?
对于以上各轴对称图形,你能找出对称轴吗?有哪些方法?
是轴对称图形,根据轴对称图形的定义,沿一条直线折叠,直线两侧的图形可以重合
如图为各图形的对称轴,用对折的方法
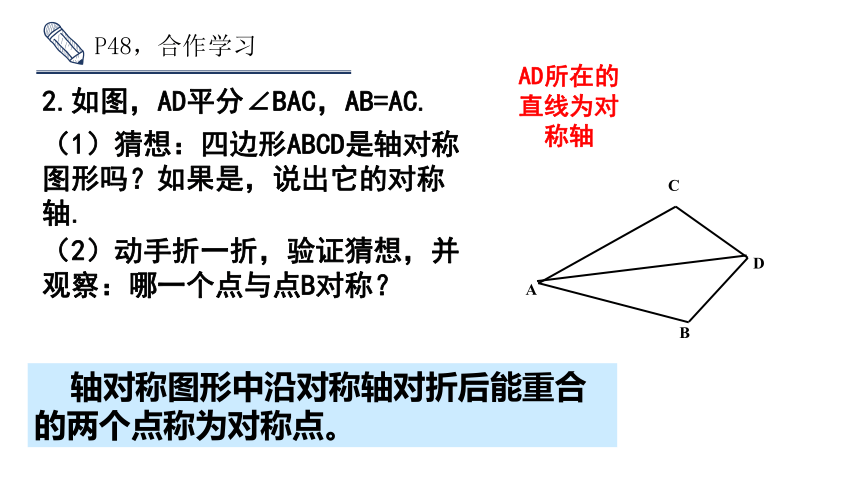
P48,合作学习
下列四个图案,其中轴对称图形有( )
B
A.0个 B.1个 C.2个 D.3个
针对训练
2.如图,AD平分∠BAC,AB=AC.
AD所在的直线为对称轴
A
B
C
D
(1)猜想:四边形ABCD是轴对称图形吗?如果是,说出它的对称轴.
(2)动手折一折,验证猜想,并观察:哪一个点与点B对称?
轴对称图形中沿对称轴对折后能重合的两个点称为对称点。
P48,合作学习
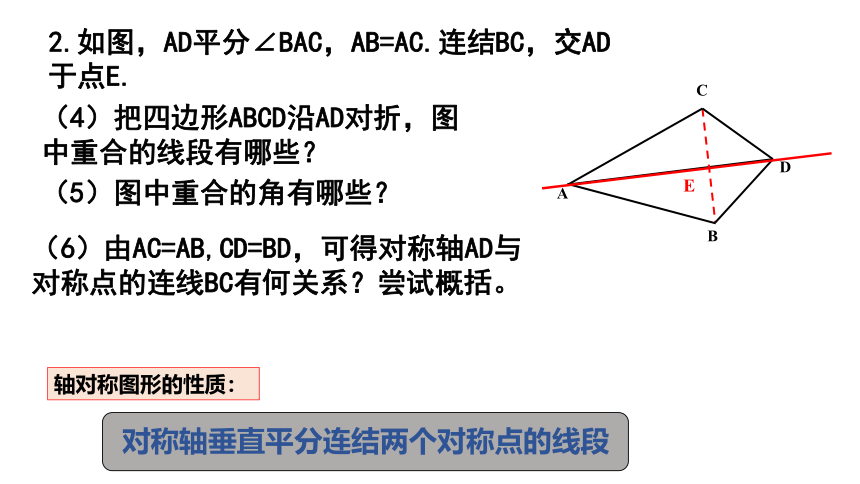
2.如图,AD平分∠BAC,AB=AC.连结BC,交AD于点E.
(6)由AC=AB,CD=BD,可得对称轴AD与对称点的连线BC有何关系?尝试概括。
E
A
B
C
D
(4)把四边形ABCD沿AD对折,图中重合的线段有哪些?
(5)图中重合的角有哪些?
对称轴垂直平分连结两个对称点的线段
轴对称图形的性质:
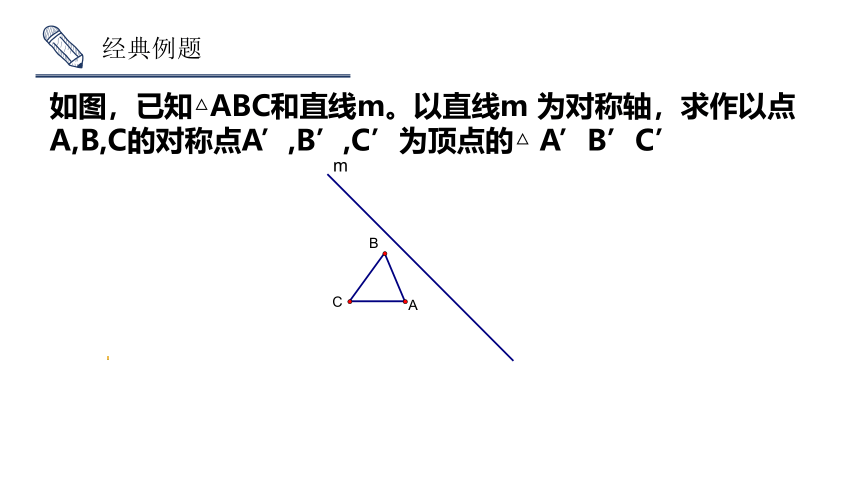
如图,已知△ABC和直线m。以直线m 为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’
m
B
C
A
经典例题
几何图形都可以看做由点组成,
找:
描点:
连线:
画对称图形的方法
找出已知图形关键点;
从各关键点作对称轴的垂线;
延长这个垂线,在对称轴另外一边,找一个点到这个垂直交点的距离和这边的一样长;
按照已知图形的形状,依次地把各对应点连结起来。
已知对称轴 和线段AB,画出线段AB关于直线l的对称点A′B′。
A'
B'
A
B
B'
B
A
A'
B
A
B‘
A’
针对训练
1、垂直
2、延长
3、相等
图形的轴对称有下面的性质:
1、成轴对称的图形不改变原图形的形状和大小.
2、成轴对称的两个图形是全等图形.
请同学们观察例1画的两个三角形,以及下面几组图形,有什么共同特征?
新课讲解
轴对称 轴对称图形
区 别 图形 两个图形之间的对称关系 一个图形自身的对称特征
对称点位置 在两个图形上 在同一个图形上
对称轴条数 一条 至少一条
联 系 1.都沿某直线翻折后能够互相重合; 2.它们可以互相转化;如果把轴对称的两个图形看作一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两个部分,那么两个部分就是关于这条对称轴成轴对称
新课讲解
轴对称和轴对称图形的区别和联系
例2 如图,直线l表示草原上的一条河流.一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中. 他沿怎样的路线行走,能使路程最短?作出这条最短路线.
思考:
2.A,B两点连线是否经过l上一点?为什么?
3.l的另一侧是否存在点A',使l上的任意一点P满足PA=PA' 此时点A与A'有何位置关系?
4.由此,你能顺利解决问题了吗
1.关于“最短”,你学过哪些相关知识?
经典例题
设P是直线l上任意一点,连结AP,A’P
由作图知,直线l垂直平分AA’
则AC=A’C,AP=A’P(线段垂直平分线上的点到线段两端的距离相等)
∴ AP+BP=A’P+BP≥A’B
A’B=A’C+BC=AC+BC
即AP+BP≥AC+BC
所以沿折线A-C-B的路线行走时路程最短。
B
A
A’
C
P
经典例题
作点A关于直线l的对称点A’,连结A’B, 交直线l于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短.
最短路径问题解题思路的归纳
类型1 一线异侧两点
解决问题步骤
1、作对称点:作点关于直线的对称点(垂直平分);
2、转化:运用轴对称把直线同侧的两点转化为直线异侧的两点;
3、连线:两点之间,线段最短。
类型2 一线同侧两点
在∠ABC内有一点P,问:能否在BA,BC边上各找到一点M,N,使△PMN的周长最短?若能,请画图说明;若不能,说明理由.
针对练习
类型3 两线间一点
解决问题步骤
1、分别作这点关于两线的对称点;
2、连接两对称点交两线于两点,交点即为所求。
最短路径问题解题思路的归纳
1.观察下列图形,从图案看是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
C
基础巩固
基础巩固
2、如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为 .
课堂梳理
两个概念
两条性质
两类应用
1、轴对称图形
2、图形的轴对称
轴对称图形的性质;
图形的轴对称性质
1.化轴对称图形;
2.找最短路径
2.1 图形的轴对称
沿着一条直线折叠后,直线两侧的部分能够相互重合
导入新课
这条直线叫做对称轴。
轴对称图形
新课讲解
对称轴
轴对称图形:把一个图形沿着一条直线折叠后,直线两侧的部分能够相互重合,那么这个图形叫做轴对称图形。
新课讲解
① 判断一个平面图形是不是轴对称图形的关键依据是什么?
② 在这些轴对称图形中,有几条对称轴?
1.下列图形是轴对称图形吗?你是怎么判别的?
对于以上各轴对称图形,你能找出对称轴吗?有哪些方法?
是轴对称图形,根据轴对称图形的定义,沿一条直线折叠,直线两侧的图形可以重合
如图为各图形的对称轴,用对折的方法
P48,合作学习
下列四个图案,其中轴对称图形有( )
B
A.0个 B.1个 C.2个 D.3个
针对训练
2.如图,AD平分∠BAC,AB=AC.
AD所在的直线为对称轴
A
B
C
D
(1)猜想:四边形ABCD是轴对称图形吗?如果是,说出它的对称轴.
(2)动手折一折,验证猜想,并观察:哪一个点与点B对称?
轴对称图形中沿对称轴对折后能重合的两个点称为对称点。
P48,合作学习
2.如图,AD平分∠BAC,AB=AC.连结BC,交AD于点E.
(6)由AC=AB,CD=BD,可得对称轴AD与对称点的连线BC有何关系?尝试概括。
E
A
B
C
D
(4)把四边形ABCD沿AD对折,图中重合的线段有哪些?
(5)图中重合的角有哪些?
对称轴垂直平分连结两个对称点的线段
轴对称图形的性质:
如图,已知△ABC和直线m。以直线m 为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’
m
B
C
A
经典例题
几何图形都可以看做由点组成,
找:
描点:
连线:
画对称图形的方法
找出已知图形关键点;
从各关键点作对称轴的垂线;
延长这个垂线,在对称轴另外一边,找一个点到这个垂直交点的距离和这边的一样长;
按照已知图形的形状,依次地把各对应点连结起来。
已知对称轴 和线段AB,画出线段AB关于直线l的对称点A′B′。
A'
B'
A
B
B'
B
A
A'
B
A
B‘
A’
针对训练
1、垂直
2、延长
3、相等
图形的轴对称有下面的性质:
1、成轴对称的图形不改变原图形的形状和大小.
2、成轴对称的两个图形是全等图形.
请同学们观察例1画的两个三角形,以及下面几组图形,有什么共同特征?
新课讲解
轴对称 轴对称图形
区 别 图形 两个图形之间的对称关系 一个图形自身的对称特征
对称点位置 在两个图形上 在同一个图形上
对称轴条数 一条 至少一条
联 系 1.都沿某直线翻折后能够互相重合; 2.它们可以互相转化;如果把轴对称的两个图形看作一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两个部分,那么两个部分就是关于这条对称轴成轴对称
新课讲解
轴对称和轴对称图形的区别和联系
例2 如图,直线l表示草原上的一条河流.一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中. 他沿怎样的路线行走,能使路程最短?作出这条最短路线.
思考:
2.A,B两点连线是否经过l上一点?为什么?
3.l的另一侧是否存在点A',使l上的任意一点P满足PA=PA' 此时点A与A'有何位置关系?
4.由此,你能顺利解决问题了吗
1.关于“最短”,你学过哪些相关知识?
经典例题
设P是直线l上任意一点,连结AP,A’P
由作图知,直线l垂直平分AA’
则AC=A’C,AP=A’P(线段垂直平分线上的点到线段两端的距离相等)
∴ AP+BP=A’P+BP≥A’B
A’B=A’C+BC=AC+BC
即AP+BP≥AC+BC
所以沿折线A-C-B的路线行走时路程最短。
B
A
A’
C
P
经典例题
作点A关于直线l的对称点A’,连结A’B, 交直线l于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短.
最短路径问题解题思路的归纳
类型1 一线异侧两点
解决问题步骤
1、作对称点:作点关于直线的对称点(垂直平分);
2、转化:运用轴对称把直线同侧的两点转化为直线异侧的两点;
3、连线:两点之间,线段最短。
类型2 一线同侧两点
在∠ABC内有一点P,问:能否在BA,BC边上各找到一点M,N,使△PMN的周长最短?若能,请画图说明;若不能,说明理由.
针对练习
类型3 两线间一点
解决问题步骤
1、分别作这点关于两线的对称点;
2、连接两对称点交两线于两点,交点即为所求。
最短路径问题解题思路的归纳
1.观察下列图形,从图案看是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
C
基础巩固
基础巩固
2、如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小;
(3)四边形BCC1B1的面积为 .
课堂梳理
两个概念
两条性质
两类应用
1、轴对称图形
2、图形的轴对称
轴对称图形的性质;
图形的轴对称性质
1.化轴对称图形;
2.找最短路径
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
