浙教版八年级上册 2.7 探索勾股定理 课件(共25张)
文档属性
| 名称 | 浙教版八年级上册 2.7 探索勾股定理 课件(共25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 18:18:28 | ||
图片预览




文档简介
(共25张PPT)
2.7 勾股定理(1)
观察
(1) ΔABC的形状
(2)正方形M面积是
个单位面积。
正方形N的面积是
个单位面积。
正方形L的面积是
个单位面积。
AC2=16
BC2=9
M
N
L
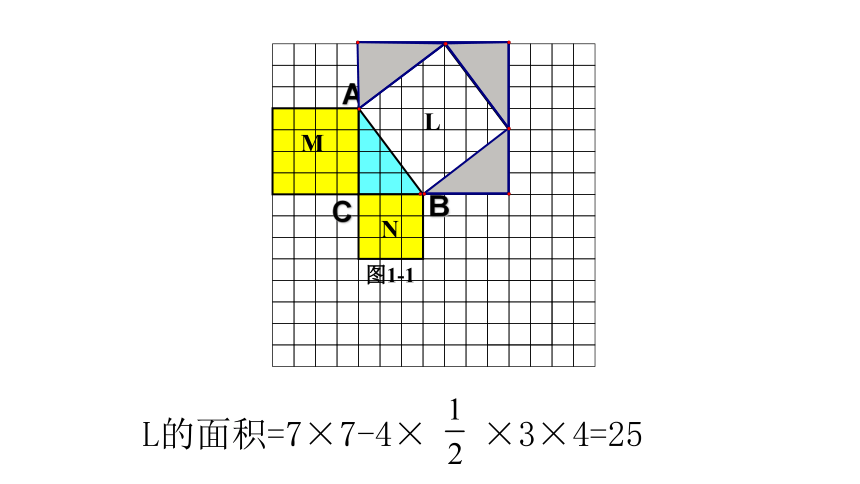
图1-1
(图中每个小方格代表一个单位面积)
A
B
C
预学展示
M
N
L
图1-1
A
B
C
L的面积=7×7-4× ×3×4=25
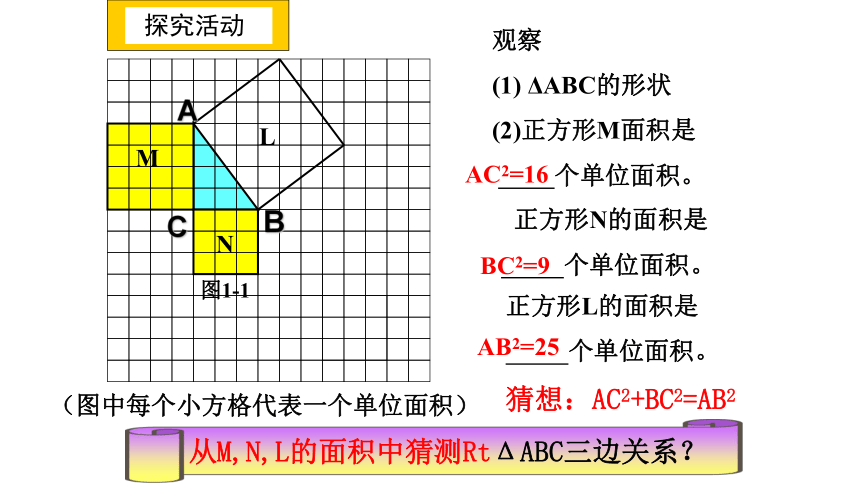
观察
(1) ΔABC的形状
(2)正方形M面积是
个单位面积。
正方形N的面积是
个单位面积。
正方形L的面积是
个单位面积。
AC2=16
BC2=9
AB2=25
从M,N,L的面积中猜测RtΔABC三边关系?
M
N
L
图1-1
(图中每个小方格代表一个单位面积)
A
B
C
探究活动
猜想:AC2+BC2=AB2
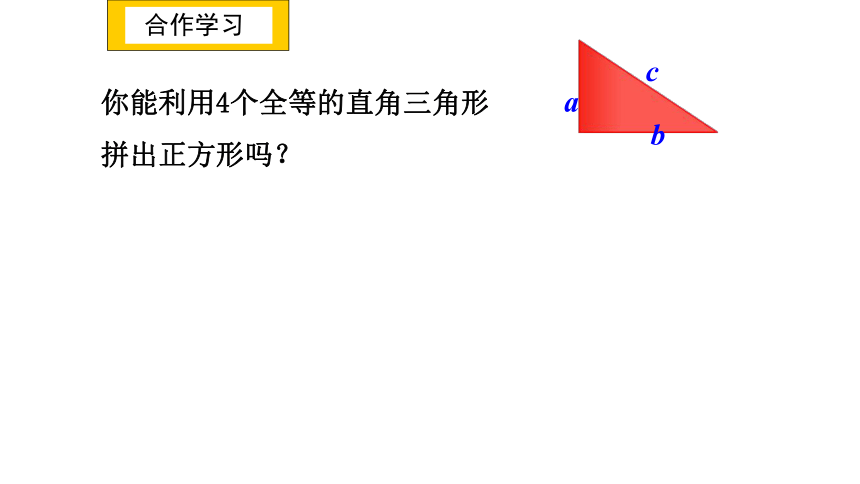
合作学习
你能利用4个全等的直角三角形
拼出正方形吗?
合作学习
利用4个全等的直角三角形
拼出下列两组图形
验证: 如何证明a、b、c的关系?—— 面积法
猜想:a2+b2=c2
c
a
b
c
a
b
c
a
b
c
a
b
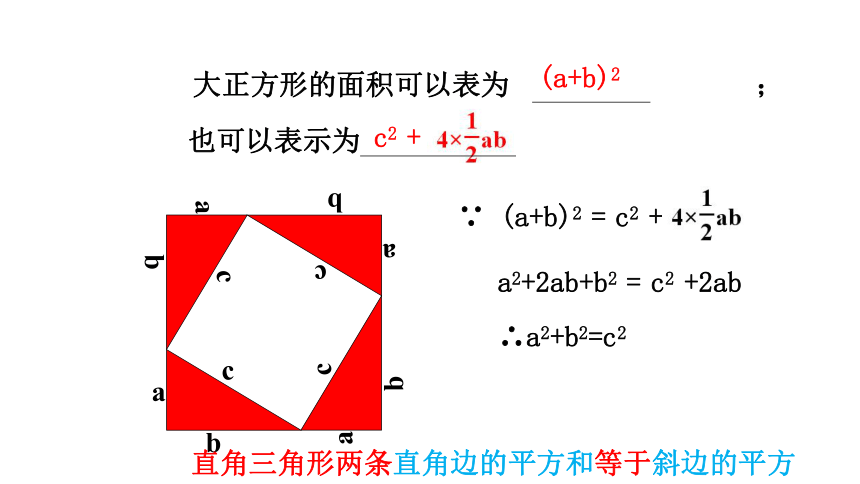
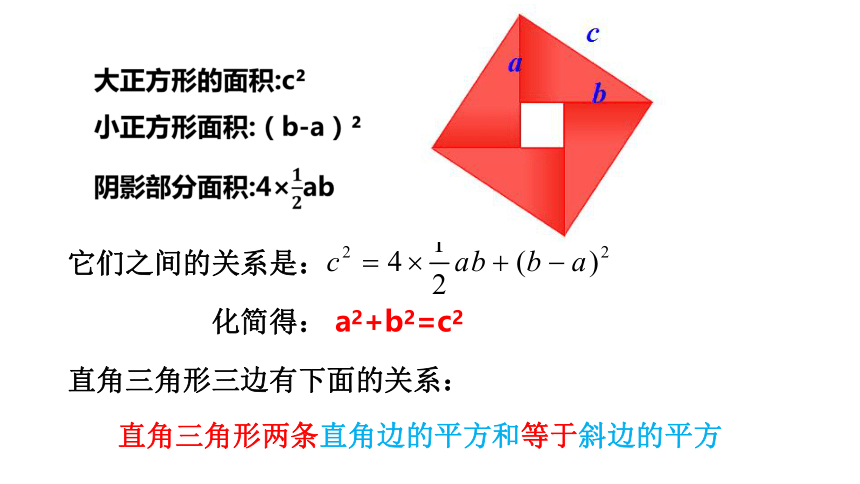
∵ (a+b)2 = c2 +
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表为 ;
(a+b)2
c2 +
也可以表示为
直角三角形两条直角边的平方和等于斜边的平方
a2+b2=c2
它们之间的关系是:
化简得:
直角三角形三边有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形三边关系:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
发现新知
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
知识链接
例题讲解
看看谁算得快
!
8
x
17
82+x2=172
52+122=x2
∴x2=172-82
=225
又∵x>0
∴x=15
∴x2=52+122
=169
又∵x>0
∴x=13
可用勾股定理建立方程.
方法小结:
由勾股定理得:
由勾股定理得:
12
5
x
学以致用
图(1)
图(2)
图(3)
由勾股定理得:
32+42=25=52
∴52+122=x2
=169
又∵x>0
∴x=13
(1)若a=1, b=2, 求c;
已知ΔABC中,∠C=Rt∠,BC=a,AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=34,a:b=8:15,求a、b;
注意:应用勾股定理要分清直角边、斜边
小心有诈
一个长方形零件图,根据所给的尺寸 (单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
探究活动1
解:作△ABC如图
则AC=90-40=50mm
BC=160-40=120mm
∴
在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
这道题的意思是说:有一个边长为1丈的正方形水池,在池的正中央长
着一根芦苇,芦苇露出
水面1尺.若将芦苇拉
到池边中点处,芦苇的
顶端恰好与水面齐平.
问水有多深?芦苇有多
长(1丈=10尺)?
请你解决这个问题.
提示:建立模型,借助方程
数学与生活
C
D
B
A
提示:建立模型,借助方程
1
5
x
x+1
解:设水深x尺,则芦苇长(x+1)尺.
由题意,得x2+52=(x+1)2,解得 x=12,
答:水深12尺,芦苇长13尺.
在平静的湖面上,有一支红莲,高出水面1尺红莲被风一吹,花朵刚好与水面平齐,已知红莲移动的水平距离是2尺,问这里水深是多少?
数学与生活
C
D
B
A
提示:建立模型,借助方程
1
2
x
x+1
x2+22=(x+1)2
如图,在△ABC中,AB=AC。已知AB=17,BC=16。
(1)求BC边上的中线AD的长。
(2)求△ABC的面积。
(3)过点B作BE⊥AC,垂足为E,求BE的长。
E
解:∵AB=AC
∴△ABC为等腰三角形
∵AD为底边中线,
∴AD⊥BC(等腰三角形三线合一)
∴△ADB为Rt△
∵AB=17,BC=16 即BD=8
∴
解:∵AD=15(已求) BC=16(已知)
∴S△ABC=15×16÷2=120
提示:利用等面积法
用刻度尺和圆规画一条线段,使它的长度等于
3
2
驶向胜利的彼岸
探究活动2
1、在数轴上画出表示 的点。
A
1
1
2、数轴上点A表示的数是什么?
O
这节课我们学习了:
1.勾股定理的证明:
2.勾股定理:
3.勾股定理的应用:
21cnjy.com
课堂小结
猜想
a2+b2=c2
验证
直角三角形两直角边的平方和等于斜边的平方
建立模型,借助方程
如图图中数字所表示的正方形的面积,
则正方形B所表示的面积为 .
B
225
81
灵活运用
144
a
b
c
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,折痕与CD边交于点E,已知AB=8cm,BC=10cm,求EC的长.
F
E
D
C
B
A
拓展提升
2.7 勾股定理(1)
观察
(1) ΔABC的形状
(2)正方形M面积是
个单位面积。
正方形N的面积是
个单位面积。
正方形L的面积是
个单位面积。
AC2=16
BC2=9
M
N
L
图1-1
(图中每个小方格代表一个单位面积)
A
B
C
预学展示
M
N
L
图1-1
A
B
C
L的面积=7×7-4× ×3×4=25
观察
(1) ΔABC的形状
(2)正方形M面积是
个单位面积。
正方形N的面积是
个单位面积。
正方形L的面积是
个单位面积。
AC2=16
BC2=9
AB2=25
从M,N,L的面积中猜测RtΔABC三边关系?
M
N
L
图1-1
(图中每个小方格代表一个单位面积)
A
B
C
探究活动
猜想:AC2+BC2=AB2
合作学习
你能利用4个全等的直角三角形
拼出正方形吗?
合作学习
利用4个全等的直角三角形
拼出下列两组图形
验证: 如何证明a、b、c的关系?—— 面积法
猜想:a2+b2=c2
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 +
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表为 ;
(a+b)2
c2 +
也可以表示为
直角三角形两条直角边的平方和等于斜边的平方
a2+b2=c2
它们之间的关系是:
化简得:
直角三角形三边有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形三边关系:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
发现新知
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
知识链接
例题讲解
看看谁算得快
!
8
x
17
82+x2=172
52+122=x2
∴x2=172-82
=225
又∵x>0
∴x=15
∴x2=52+122
=169
又∵x>0
∴x=13
可用勾股定理建立方程.
方法小结:
由勾股定理得:
由勾股定理得:
12
5
x
学以致用
图(1)
图(2)
图(3)
由勾股定理得:
32+42=25=52
∴52+122=x2
=169
又∵x>0
∴x=13
(1)若a=1, b=2, 求c;
已知ΔABC中,∠C=Rt∠,BC=a,AC=b,AB=c。
(2)若a=15,c=17,求b;
(3)若c=34,a:b=8:15,求a、b;
注意:应用勾股定理要分清直角边、斜边
小心有诈
一个长方形零件图,根据所给的尺寸 (单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
探究活动1
解:作△ABC如图
则AC=90-40=50mm
BC=160-40=120mm
∴
在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
这道题的意思是说:有一个边长为1丈的正方形水池,在池的正中央长
着一根芦苇,芦苇露出
水面1尺.若将芦苇拉
到池边中点处,芦苇的
顶端恰好与水面齐平.
问水有多深?芦苇有多
长(1丈=10尺)?
请你解决这个问题.
提示:建立模型,借助方程
数学与生活
C
D
B
A
提示:建立模型,借助方程
1
5
x
x+1
解:设水深x尺,则芦苇长(x+1)尺.
由题意,得x2+52=(x+1)2,解得 x=12,
答:水深12尺,芦苇长13尺.
在平静的湖面上,有一支红莲,高出水面1尺红莲被风一吹,花朵刚好与水面平齐,已知红莲移动的水平距离是2尺,问这里水深是多少?
数学与生活
C
D
B
A
提示:建立模型,借助方程
1
2
x
x+1
x2+22=(x+1)2
如图,在△ABC中,AB=AC。已知AB=17,BC=16。
(1)求BC边上的中线AD的长。
(2)求△ABC的面积。
(3)过点B作BE⊥AC,垂足为E,求BE的长。
E
解:∵AB=AC
∴△ABC为等腰三角形
∵AD为底边中线,
∴AD⊥BC(等腰三角形三线合一)
∴△ADB为Rt△
∵AB=17,BC=16 即BD=8
∴
解:∵AD=15(已求) BC=16(已知)
∴S△ABC=15×16÷2=120
提示:利用等面积法
用刻度尺和圆规画一条线段,使它的长度等于
3
2
驶向胜利的彼岸
探究活动2
1、在数轴上画出表示 的点。
A
1
1
2、数轴上点A表示的数是什么?
O
这节课我们学习了:
1.勾股定理的证明:
2.勾股定理:
3.勾股定理的应用:
21cnjy.com
课堂小结
猜想
a2+b2=c2
验证
直角三角形两直角边的平方和等于斜边的平方
建立模型,借助方程
如图图中数字所表示的正方形的面积,
则正方形B所表示的面积为 .
B
225
81
灵活运用
144
a
b
c
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,折痕与CD边交于点E,已知AB=8cm,BC=10cm,求EC的长.
F
E
D
C
B
A
拓展提升
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
