浙教版八年级下册 4.3 中心对称 课件(共22张PPT)
文档属性
| 名称 | 浙教版八年级下册 4.3 中心对称 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 19:44:28 | ||
图片预览








文档简介
(共22张PPT)
这一组图片具有什么共同的特点?可称之为什么图形?
你认识这些车标吗?
第二组图片具有什么共同的特点?可称之为什么图形?
轴对称图形
C
O/
D
A
B
如图,点O是等边三角形ABC的两条高的交点. 以O为旋转中心,把等边三角形ABC按顺时针方向旋转180o,作出所得的像.
点O/是平行四边形ABCD的对角线AC,BD的交点.以O/为旋转中心,把平行四边形ABCD按顺时针方向旋转1800作出所得的像.
C
A
B
你发现了什么
O/
O
观察比较
(A)
(B)
(C)
(A)
(C)
(B)
(D)
新知—定义
(A)
(C)
(B)
(D)
如果一个图形绕着一个点旋转180。后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形。
对称中心
互相重合的两个点是一对对称点
(A)
(B)
(C)
中心对称图形
问题解决
A
O
巩固运用
A
A’
O
O
A
1、下列图形(或图标)是中心对称图形吗?如果是的话找出对称中心。
A’
A’
B
两对对称点连接的线段的交点即是对称中心
O
A
B
C
E
F
D
如果一个图形绕着一个点O旋转180°,能够和另外一个图形互相重合,就称这两个图形关于点O成中心对称。
提出问题
新知—定义
A
E
F
D
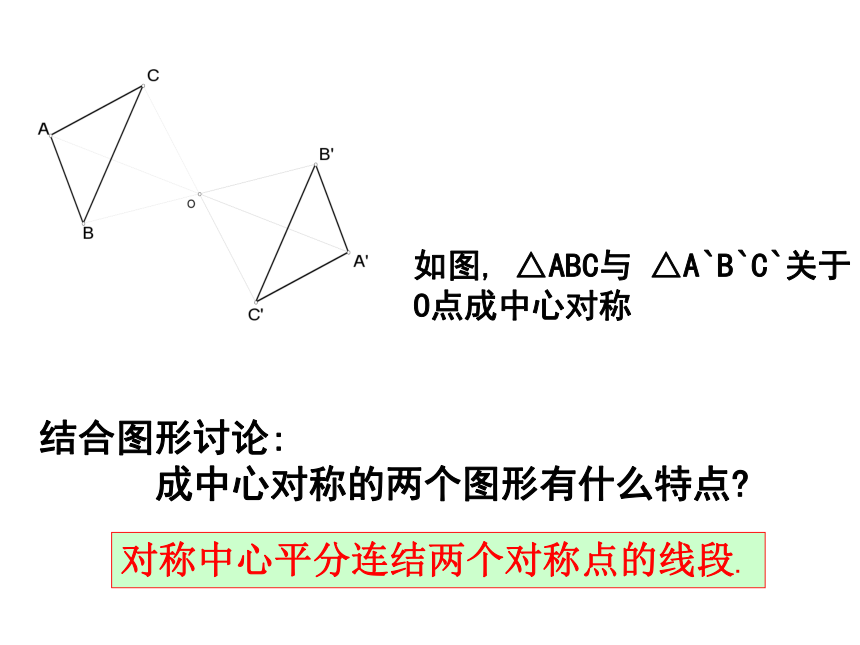
这两个三角形之间有什么关系?
结合图形讨论:
成中心对称的两个图形有什么特点
如图, △ABC与 △A`B`C`关于
O点成中心对称
对称中心平分连结两个对称点的线段.
A
O
A'
连结OA,
并延长到A’,使OA’=OA,
已知A点和O点,画出点A关于点O的对称点A'
则A’是所求的点
新知—应用
例1、如图,已知△ABC 和点O,作△ A'B'C' ,使△A'B'C'与△ABC关于点O成中心对称。
(2)同理,作出点B,C的对称点B/,C/;
解:(1)连结AO关延长到A/,使AO=A/O;
(3)连结A/B/.B/C/,C/A/,则⊿A/B/C/即为所求的三角形.
A
B
C
O
A′
C′
B′
新知—应用
对称中心平分连结两个对称点的线段.
点
线
面
B
A
C
B’
A’
作出
关于点C成中心对称的图形。
变式1:
新知—应用
O
B
A
C
A ′
C ′
B′
变式2:已知△ABC和点O,作△A'B'C',使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
O
B
A
C
A ′
C ′
B′
变式3:已知△ABC和点O,作△A'B'C',使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
例2:求证:在直角坐标系中,点A (x , y)与点B(-x , -y)关于原点成中心对称。
A (x , y)
B(-x , -y)
O
C
D
在直角坐标系中,点A (x , y)与
点B(-x , -y)关于原点成中心对称。
轴对称图形 成轴对称
是一个图形
是一种图形变换,
包含两个图形
都有对称轴,翻折后都会重合
如果把关于某条直线成轴对称的两个图形看成一个整体,则这个整体为轴对称图形.
对比轴对称图形与成轴对称:
比较归纳
A
B
C
(B)
不同点
联系
A
B
C
A’
B’
C’
图形
相同点
中心对称图形 成中心对称
是一个图形
是一种图形变换,
包含两个图形
都有旋转中心,旋转180°后都会重合
如果把关于某个点成中心对称的两个图形看成一个整体,则这个整体为中心对称图形.
对比中心对称图形与成中心对称:
类比归纳
图形
不同点
联系
相同点
比较归纳
A
B
C
A’
B’
C’
轴 对 称
中 心 对 称
关于线对称
关于点对称
回顾总结
谈谈学习的内容与方法
2个定义:
1种方法:
1个性质:
2个应用:
中心对称图形的定义,
成中心对称的定义,.
对称中心平分连结两个对称点的线段.
作图
平面直角坐标系
类比归纳
1.如图是五个小正方形拼成的图形.请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的新图形:
(1)是中心对称图形,但不是轴对称图形
(2)既是轴对称图形,又是中心对称图形
(1)
(2)
拓展提升
2、如图平行四边形ABCD,画一条直线将其面积二等分,你有多少种不同的方法?
变式:如图 ,如何用一条直线将其面积二等分?
拓展提升
*
具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体,能够在所在的平面内绕对称中心平稳旋转。所以在生产中,有关旋转的零部件常设计成中心对称图形。
中心对称的特征与实际应用
这一组图片具有什么共同的特点?可称之为什么图形?
你认识这些车标吗?
第二组图片具有什么共同的特点?可称之为什么图形?
轴对称图形
C
O/
D
A
B
如图,点O是等边三角形ABC的两条高的交点. 以O为旋转中心,把等边三角形ABC按顺时针方向旋转180o,作出所得的像.
点O/是平行四边形ABCD的对角线AC,BD的交点.以O/为旋转中心,把平行四边形ABCD按顺时针方向旋转1800作出所得的像.
C
A
B
你发现了什么
O/
O
观察比较
(A)
(B)
(C)
(A)
(C)
(B)
(D)
新知—定义
(A)
(C)
(B)
(D)
如果一个图形绕着一个点旋转180。后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形。
对称中心
互相重合的两个点是一对对称点
(A)
(B)
(C)
中心对称图形
问题解决
A
O
巩固运用
A
A’
O
O
A
1、下列图形(或图标)是中心对称图形吗?如果是的话找出对称中心。
A’
A’
B
两对对称点连接的线段的交点即是对称中心
O
A
B
C
E
F
D
如果一个图形绕着一个点O旋转180°,能够和另外一个图形互相重合,就称这两个图形关于点O成中心对称。
提出问题
新知—定义
A
E
F
D
这两个三角形之间有什么关系?
结合图形讨论:
成中心对称的两个图形有什么特点
如图, △ABC与 △A`B`C`关于
O点成中心对称
对称中心平分连结两个对称点的线段.
A
O
A'
连结OA,
并延长到A’,使OA’=OA,
已知A点和O点,画出点A关于点O的对称点A'
则A’是所求的点
新知—应用
例1、如图,已知△ABC 和点O,作△ A'B'C' ,使△A'B'C'与△ABC关于点O成中心对称。
(2)同理,作出点B,C的对称点B/,C/;
解:(1)连结AO关延长到A/,使AO=A/O;
(3)连结A/B/.B/C/,C/A/,则⊿A/B/C/即为所求的三角形.
A
B
C
O
A′
C′
B′
新知—应用
对称中心平分连结两个对称点的线段.
点
线
面
B
A
C
B’
A’
作出
关于点C成中心对称的图形。
变式1:
新知—应用
O
B
A
C
A ′
C ′
B′
变式2:已知△ABC和点O,作△A'B'C',使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
O
B
A
C
A ′
C ′
B′
变式3:已知△ABC和点O,作△A'B'C',使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
例2:求证:在直角坐标系中,点A (x , y)与点B(-x , -y)关于原点成中心对称。
A (x , y)
B(-x , -y)
O
C
D
在直角坐标系中,点A (x , y)与
点B(-x , -y)关于原点成中心对称。
轴对称图形 成轴对称
是一个图形
是一种图形变换,
包含两个图形
都有对称轴,翻折后都会重合
如果把关于某条直线成轴对称的两个图形看成一个整体,则这个整体为轴对称图形.
对比轴对称图形与成轴对称:
比较归纳
A
B
C
(B)
不同点
联系
A
B
C
A’
B’
C’
图形
相同点
中心对称图形 成中心对称
是一个图形
是一种图形变换,
包含两个图形
都有旋转中心,旋转180°后都会重合
如果把关于某个点成中心对称的两个图形看成一个整体,则这个整体为中心对称图形.
对比中心对称图形与成中心对称:
类比归纳
图形
不同点
联系
相同点
比较归纳
A
B
C
A’
B’
C’
轴 对 称
中 心 对 称
关于线对称
关于点对称
回顾总结
谈谈学习的内容与方法
2个定义:
1种方法:
1个性质:
2个应用:
中心对称图形的定义,
成中心对称的定义,.
对称中心平分连结两个对称点的线段.
作图
平面直角坐标系
类比归纳
1.如图是五个小正方形拼成的图形.请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的新图形:
(1)是中心对称图形,但不是轴对称图形
(2)既是轴对称图形,又是中心对称图形
(1)
(2)
拓展提升
2、如图平行四边形ABCD,画一条直线将其面积二等分,你有多少种不同的方法?
变式:如图 ,如何用一条直线将其面积二等分?
拓展提升
*
具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体,能够在所在的平面内绕对称中心平稳旋转。所以在生产中,有关旋转的零部件常设计成中心对称图形。
中心对称的特征与实际应用
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
