浙教版八年级下册第五章特殊的平行四边形: 5.2 菱形 课件 16张PPT
文档属性
| 名称 | 浙教版八年级下册第五章特殊的平行四边形: 5.2 菱形 课件 16张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 815.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 22:04:56 | ||
图片预览




文档简介
(共16张PPT)
1.矩形的四个角都是________.
2.矩形的对角线_______.
直角
相等
3.___________________________是矩形.
有三个是直角的四边形
5.__________________________是矩形
对角线相等的平行四边形
6.矩形既是中心对称图形,又是轴对称图形.
4.___________________________是矩形.
有一个角是直角的平行四边形
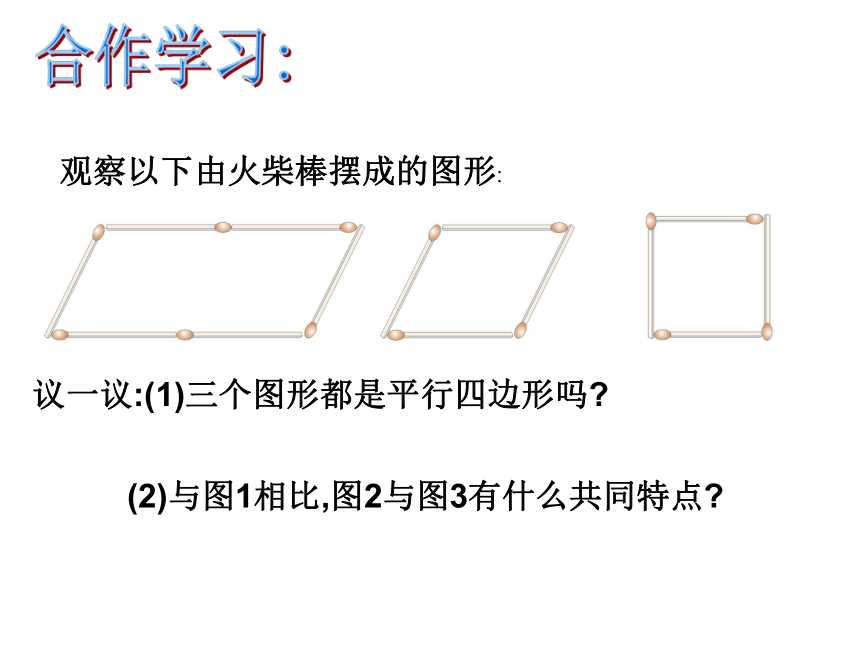
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗
(2)与图1相比,图2与图3有什么共同特点
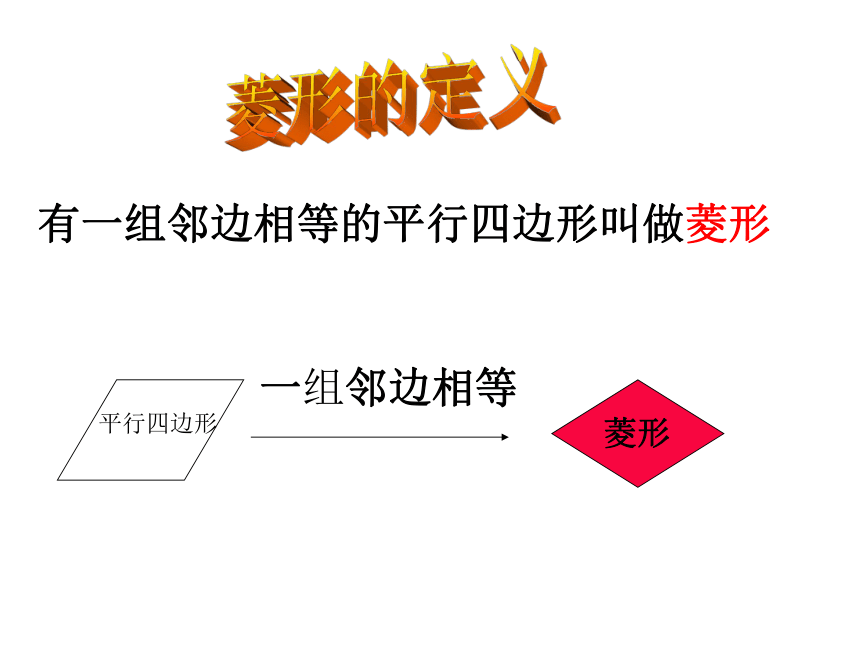
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
看一看
三菱越野汽车欣赏
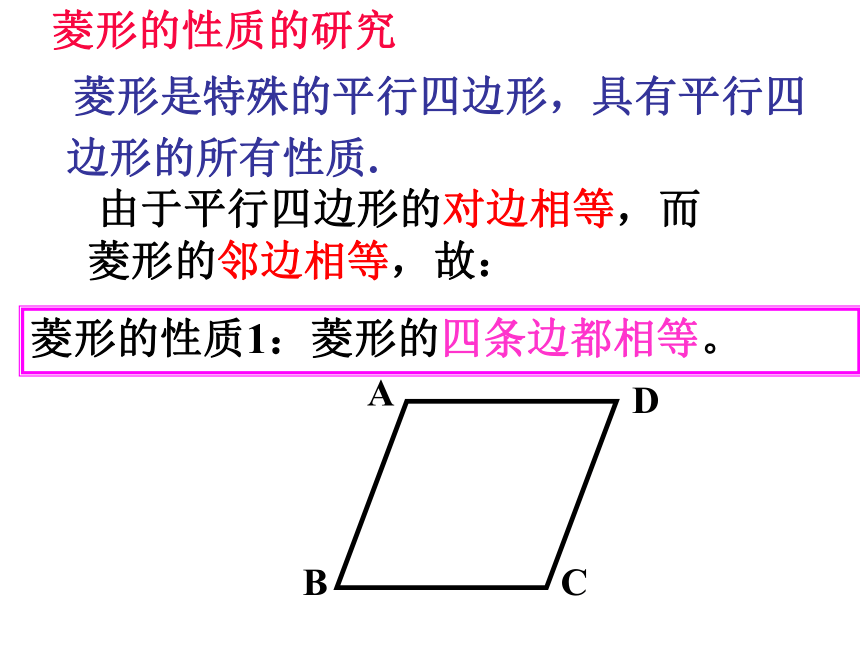
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质1:菱形的四条边都相等。
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质的研究
已知:菱形ABCD中,对角线AC,BD相交于点O.
AC⊥BD吗
AC平分∠BAD和∠ BCD吗 BD平分∠ ABC和∠ ADC吗
A
B
C
D
O
性质2.菱形的对角线相互垂直,并且每条对角线平分一组对角
这两个性质只是菱形不同于一般平行四边形的特殊性质,菱形还具有平行四边形的所有性质.
菱形的性质1:菱形的四条边都相等。
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
想一想 矩形、菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条
矩形是轴对称图形,对称轴有两条。
菱形是轴对称图形,对称轴有两条。
.
.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
A
B
C
D
O
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
D
A
B
C
O
E
S菱形=AB×DE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
ABCD=S△ABC+S△ADC= AC×BD
S菱形
面积:S菱形=底×高=对角线乘积的一半
为什么
例1变形
C
O
D
B
A
菱形ABCD的周长为16,相邻两角的度数比为1:2.
⑴求菱形ABCD的对角线的长;
⑵求菱形ABCD的面积.
一展身手
⒉菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm B.7cm
C. 5cm D.4cm
A
B
C
D
O
3
4
C
菱形的性质1:菱形的四条边都相等。
面积:S菱形=底×高=对角线乘积的一半
菱形的性质2:菱形的对角线相互垂直,并且 每条对角线平分一组对角
适用于所有的对角线垂直的四边形
挑战自我
已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系 请你通过动手操作、度量、猜想、验证等方法予以探索。
1.矩形的四个角都是________.
2.矩形的对角线_______.
直角
相等
3.___________________________是矩形.
有三个是直角的四边形
5.__________________________是矩形
对角线相等的平行四边形
6.矩形既是中心对称图形,又是轴对称图形.
4.___________________________是矩形.
有一个角是直角的平行四边形
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗
(2)与图1相比,图2与图3有什么共同特点
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
看一看
三菱越野汽车欣赏
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质1:菱形的四条边都相等。
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质的研究
已知:菱形ABCD中,对角线AC,BD相交于点O.
AC⊥BD吗
AC平分∠BAD和∠ BCD吗 BD平分∠ ABC和∠ ADC吗
A
B
C
D
O
性质2.菱形的对角线相互垂直,并且每条对角线平分一组对角
这两个性质只是菱形不同于一般平行四边形的特殊性质,菱形还具有平行四边形的所有性质.
菱形的性质1:菱形的四条边都相等。
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
想一想 矩形、菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条
矩形是轴对称图形,对称轴有两条。
菱形是轴对称图形,对称轴有两条。
.
.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
A
B
C
D
O
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗
菱形
D
A
B
C
O
E
S菱形=AB×DE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗
ABCD=S△ABC+S△ADC= AC×BD
S菱形
面积:S菱形=底×高=对角线乘积的一半
为什么
例1变形
C
O
D
B
A
菱形ABCD的周长为16,相邻两角的度数比为1:2.
⑴求菱形ABCD的对角线的长;
⑵求菱形ABCD的面积.
一展身手
⒉菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm B.7cm
C. 5cm D.4cm
A
B
C
D
O
3
4
C
菱形的性质1:菱形的四条边都相等。
面积:S菱形=底×高=对角线乘积的一半
菱形的性质2:菱形的对角线相互垂直,并且 每条对角线平分一组对角
适用于所有的对角线垂直的四边形
挑战自我
已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系 请你通过动手操作、度量、猜想、验证等方法予以探索。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
