浙教版八年级下册数学 第二章 一元二次方程复习课件(共27张PPT)
文档属性
| 名称 | 浙教版八年级下册数学 第二章 一元二次方程复习课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 23:32:18 | ||
图片预览








文档简介
(共27张PPT)
一元二次方程
复习
现计划在校门口建造一个面积为20平方米,长比宽多1米的长方形喷水池,则它的宽为多少米?
解:
设这个喷水池的宽为x米,
x
则长为(x+1)米,
x+1
根据题意得:
x ( x+1) = 20
即 x 2 + x - 20 = 0
x + x - 20 = 0
2
观察方程
③等号两边都是整式
①只含有一个未知数
②未知数的最高次数是2次
这样的方程叫
一元二次方程
特征如下:
有何特征?
(1) 2x = y 2 - 1
(3) x 2- - 3 = 0
2
x
(4) x2+3x+4= 0
(5) x 2 = -3
结论:以上方程中(2)、(4)、(5)、(6)是一元二次方程
(6) ( x + 2) 2 = 4
请判断下列方程是否为一元二次方程:
一元二次方程的一般形式
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
-7
1
0
说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式
X-7x2=0的二次项系数、一次项系数、常数项分别是多少?
(2011甘肃兰州,第1题)下列方程中是关于x的一元二次方程的是( )
A. B.
C. D.
C
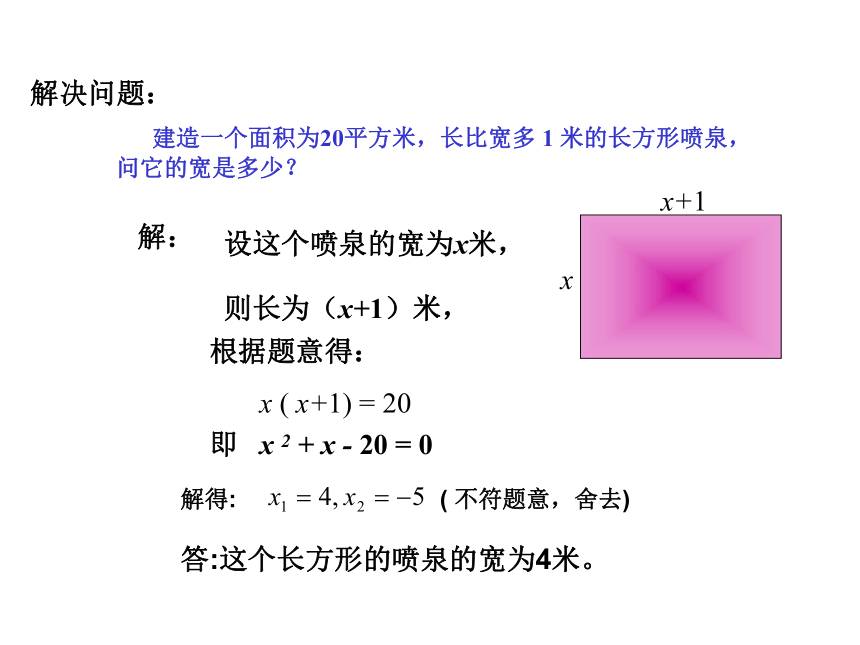
解决问题:
建造一个面积为20平方米,长比宽多 1 米的长方形喷泉,问它的宽是多少?
解:
设这个喷泉的宽为x米,
x
则长为(x+1)米,
x+1
根据题意得:
x ( x+1) = 20
即 x 2 + x - 20 = 0
解得:
答:这个长方形的喷泉的宽为4米。
( 不符题意,舍去)
一元二次方程的解法
1.因式分解法
2.开平方法
3.配方法
4.公式法
二次项系数为1,而一次项系数为偶数
用适当的方法解下列方程
因式分解法:
对于缺少常数项的一元二次方程,
用因式分解法比较方便;
形如:ax2+bx=o(即常数c=0).
因式分解法的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
x1=0,x2=3
开平方法:
对于缺少一次项的一元二次方程,用开平方法比较方便;
形如:
ax2+c=o 或a(x+m)2=k
X1=-1, x2=2
配方法:
用配方法的条件是:
适应于任何一元二次方程。
但是除了形如x2+2kx+c=0 用配方法外,一般不用;
(即二次项系数为1,一次项系数是偶数)
配方法的一般步骤:
三配----方程两边都加 ______________,
使等号左边构成完全平方式
一除----把二次项系数化为1(方程的两边同时除以二次项系数a)
二移----把常数项移到方程的右边;
四开----利用开平方法求出原方程的两个解.
一次项系数一半的平方
公式法:
用公式法的条件是:
适应于任何一元二次方程。
先将方程化为一般形式,
再用公式求解。
方程根的情况与b2—4ac
的值的关系:
当b2-4ac>0 时,方程有两个不相等的实数根;
当b2-4ac=0 时,方程有两个相等的实数根;
当b2-4ac<0 时,方程没有实数根.
(2011重庆江津区,第9题)
已知关于x的一元二次方程(a﹣l)x2﹣2x+l=0有两个不相等的实数根,则a的取值范围是( )
A、a<2 B、a>2 C、a<2且a≠l D、a<﹣2
说明:当方程为一元二次方程,且二次项系数含有字母时,要注意二次项系数不能为0。
c
阅读下列的解答过程,请判断是否有错,若有错误,请你写出正确答案。
解: x (x-3) =2 (x-3)
两边同除以(x-3) 得: x =2
说明:方程的两边有相同的含有未知数的因式时,不能两边都除以这个因式,因为这样能把方程的一个根丢失了,要利用因式分解法求解。
x1=3 x2=2
阅读材料,解答问题
为了解方程x4 +x2-2=0,我们将x2视为一个整体,
解:设 x2 =a,则x4 =a
原方程可化为 a +a-2=0
a1=1,a2=-2。
当a=1时,x =1,x =±1
当a=-2时, x =-2 ,方程无解
∴x1=1 ,x2 =-1
在上述的解答过程中,利用了 法
达到了降次的目的,体现了 的数学思想。
换元
转化(化归)
反思:遇到高次(大于2次)的方程,可利用了换元法达到了降次的目的
在科技楼后一块长320米,宽200米的长方形空地上,计划修筑横竖各1条笔直等宽的鹅卵石路,余下部分铺上草坪,作为4块大小不一的高尔夫球场。请你在这块空地上设计一个方案, 要求4块高尔夫球场总面积为5890m2,并求出方案中鹅卵石路的宽为多少米?
(只要求画出示意图,并求列出方程即可)
200
320
分析:利用“图形经过平移”,它的面积大小不会改变的,把纵横两条路平移一下
320
200
解:设道路的宽为 米,根据题意得,
化简:
解得 1=10, 2=500
(不符题意,舍去)
答:道路宽为10米。
答:通道的宽为1米。
解:设通道宽为x 米,则泳池的长为(32-2x)米,宽为(20-2x) 米,根据题意得:
32
20
X
X
X
X
现计划在体育馆旁建造一个长方形的露天游泳池,游泳池的四周由宽度均相等的通道围绕。整个游泳池的长和宽为分别为32米和20米(包括通道),要求游泳池的实际可游泳区为540平方米,则游泳池四周通道的宽需设计成多少米?(只要求列出方程)
解得
(不符题意,舍去)
学校要建一个长方形的科技活动基地用于航模、车模的训练,基地的需用木栏围成。到木材店买木材,老板说只要我们能帮他解决1个问题,他就可以给我们打八八折。
2010年我进了1000吨的木材,截止到现在我一共进了3310吨木材,若进货量的年增长率都相同,问年增长率为多少
(只要列出方程即可)
解:设年增长率为X,根据题意得:
答:年增长率为10%
解得:
( 不符题意,舍去)
化简:
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
(1)要使基地的面积达到150平方米,则这个长方形基地的两边长分别为多少?
X
X
40-2X
解:设长方形的一边为X米,则另一边为(40-2X)米,根据题意得:
∵30>25,不符合题意舍去。
∴长方形基地的两边为15米,10米。
解得:
(2)基地的面积能达到250平方米吗?为什么?(通过计算说明)
X
X
40-2X
解:设长方形的一边为X米,则另一边为(40-2X)米,根据题意得:
化简得:
∴方程无实数根,即长方形基地的面积不能达到250平方米。
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
解:设基地的宽为x米,
X(42-2x)=208
解得:x1=13,x2=8
答:基地的长和宽分别为16和13米。
∴长=42-2x=16或 42-2x=26>25(舍去)
(3)现在要在墙对面开一个2米宽的门,方便进出。若要使基地面积为208平方米,求基地的长和宽各是多少米
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
x
x
40-2x+2
则长为40-2x+2,即为(42-2x)米.
解:设长方形的一边为X米,则另一边为(40-2X+2),即为(42-2x)米,即根据题意得:
?
(4)现在要在墙对面开一个2米宽的门,若要使基地的面积最大,则最大面积为多少平方米?
基地一边靠着墙(假设墙足够长),另三边用长为40米的木栏围成。
x
x
40-2x+2
注意:求含有二次项和一次项的代数式最值问题时,往往需考虑配方。
答:基地的最大面积为 平方米
通过这节课的学习活动你有哪些收获?
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax +bx+c=0(a 0)
只含有一个未知数
求知数的最高次数是2
配方法
公式法
开平方法
因式分解法
二次项系数为1,而一次项系数为偶数
一元二次方程
复习
现计划在校门口建造一个面积为20平方米,长比宽多1米的长方形喷水池,则它的宽为多少米?
解:
设这个喷水池的宽为x米,
x
则长为(x+1)米,
x+1
根据题意得:
x ( x+1) = 20
即 x 2 + x - 20 = 0
x + x - 20 = 0
2
观察方程
③等号两边都是整式
①只含有一个未知数
②未知数的最高次数是2次
这样的方程叫
一元二次方程
特征如下:
有何特征?
(1) 2x = y 2 - 1
(3) x 2- - 3 = 0
2
x
(4) x2+3x+4= 0
(5) x 2 = -3
结论:以上方程中(2)、(4)、(5)、(6)是一元二次方程
(6) ( x + 2) 2 = 4
请判断下列方程是否为一元二次方程:
一元二次方程的一般形式
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
-7
1
0
说明:要确定一元二次方程的系数和常数项,必须先将方程化为一般形式
X-7x2=0的二次项系数、一次项系数、常数项分别是多少?
(2011甘肃兰州,第1题)下列方程中是关于x的一元二次方程的是( )
A. B.
C. D.
C
解决问题:
建造一个面积为20平方米,长比宽多 1 米的长方形喷泉,问它的宽是多少?
解:
设这个喷泉的宽为x米,
x
则长为(x+1)米,
x+1
根据题意得:
x ( x+1) = 20
即 x 2 + x - 20 = 0
解得:
答:这个长方形的喷泉的宽为4米。
( 不符题意,舍去)
一元二次方程的解法
1.因式分解法
2.开平方法
3.配方法
4.公式法
二次项系数为1,而一次项系数为偶数
用适当的方法解下列方程
因式分解法:
对于缺少常数项的一元二次方程,
用因式分解法比较方便;
形如:ax2+bx=o(即常数c=0).
因式分解法的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
x1=0,x2=3
开平方法:
对于缺少一次项的一元二次方程,用开平方法比较方便;
形如:
ax2+c=o 或a(x+m)2=k
X1=-1, x2=2
配方法:
用配方法的条件是:
适应于任何一元二次方程。
但是除了形如x2+2kx+c=0 用配方法外,一般不用;
(即二次项系数为1,一次项系数是偶数)
配方法的一般步骤:
三配----方程两边都加 ______________,
使等号左边构成完全平方式
一除----把二次项系数化为1(方程的两边同时除以二次项系数a)
二移----把常数项移到方程的右边;
四开----利用开平方法求出原方程的两个解.
一次项系数一半的平方
公式法:
用公式法的条件是:
适应于任何一元二次方程。
先将方程化为一般形式,
再用公式求解。
方程根的情况与b2—4ac
的值的关系:
当b2-4ac>0 时,方程有两个不相等的实数根;
当b2-4ac=0 时,方程有两个相等的实数根;
当b2-4ac<0 时,方程没有实数根.
(2011重庆江津区,第9题)
已知关于x的一元二次方程(a﹣l)x2﹣2x+l=0有两个不相等的实数根,则a的取值范围是( )
A、a<2 B、a>2 C、a<2且a≠l D、a<﹣2
说明:当方程为一元二次方程,且二次项系数含有字母时,要注意二次项系数不能为0。
c
阅读下列的解答过程,请判断是否有错,若有错误,请你写出正确答案。
解: x (x-3) =2 (x-3)
两边同除以(x-3) 得: x =2
说明:方程的两边有相同的含有未知数的因式时,不能两边都除以这个因式,因为这样能把方程的一个根丢失了,要利用因式分解法求解。
x1=3 x2=2
阅读材料,解答问题
为了解方程x4 +x2-2=0,我们将x2视为一个整体,
解:设 x2 =a,则x4 =a
原方程可化为 a +a-2=0
a1=1,a2=-2。
当a=1时,x =1,x =±1
当a=-2时, x =-2 ,方程无解
∴x1=1 ,x2 =-1
在上述的解答过程中,利用了 法
达到了降次的目的,体现了 的数学思想。
换元
转化(化归)
反思:遇到高次(大于2次)的方程,可利用了换元法达到了降次的目的
在科技楼后一块长320米,宽200米的长方形空地上,计划修筑横竖各1条笔直等宽的鹅卵石路,余下部分铺上草坪,作为4块大小不一的高尔夫球场。请你在这块空地上设计一个方案, 要求4块高尔夫球场总面积为5890m2,并求出方案中鹅卵石路的宽为多少米?
(只要求画出示意图,并求列出方程即可)
200
320
分析:利用“图形经过平移”,它的面积大小不会改变的,把纵横两条路平移一下
320
200
解:设道路的宽为 米,根据题意得,
化简:
解得 1=10, 2=500
(不符题意,舍去)
答:道路宽为10米。
答:通道的宽为1米。
解:设通道宽为x 米,则泳池的长为(32-2x)米,宽为(20-2x) 米,根据题意得:
32
20
X
X
X
X
现计划在体育馆旁建造一个长方形的露天游泳池,游泳池的四周由宽度均相等的通道围绕。整个游泳池的长和宽为分别为32米和20米(包括通道),要求游泳池的实际可游泳区为540平方米,则游泳池四周通道的宽需设计成多少米?(只要求列出方程)
解得
(不符题意,舍去)
学校要建一个长方形的科技活动基地用于航模、车模的训练,基地的需用木栏围成。到木材店买木材,老板说只要我们能帮他解决1个问题,他就可以给我们打八八折。
2010年我进了1000吨的木材,截止到现在我一共进了3310吨木材,若进货量的年增长率都相同,问年增长率为多少
(只要列出方程即可)
解:设年增长率为X,根据题意得:
答:年增长率为10%
解得:
( 不符题意,舍去)
化简:
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
(1)要使基地的面积达到150平方米,则这个长方形基地的两边长分别为多少?
X
X
40-2X
解:设长方形的一边为X米,则另一边为(40-2X)米,根据题意得:
∵30>25,不符合题意舍去。
∴长方形基地的两边为15米,10米。
解得:
(2)基地的面积能达到250平方米吗?为什么?(通过计算说明)
X
X
40-2X
解:设长方形的一边为X米,则另一边为(40-2X)米,根据题意得:
化简得:
∴方程无实数根,即长方形基地的面积不能达到250平方米。
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
解:设基地的宽为x米,
X(42-2x)=208
解得:x1=13,x2=8
答:基地的长和宽分别为16和13米。
∴长=42-2x=16或 42-2x=26>25(舍去)
(3)现在要在墙对面开一个2米宽的门,方便进出。若要使基地面积为208平方米,求基地的长和宽各是多少米
长方形的基地一边靠着长25米的墙,另三边用长为40米的木栏围成
x
x
40-2x+2
则长为40-2x+2,即为(42-2x)米.
解:设长方形的一边为X米,则另一边为(40-2X+2),即为(42-2x)米,即根据题意得:
?
(4)现在要在墙对面开一个2米宽的门,若要使基地的面积最大,则最大面积为多少平方米?
基地一边靠着墙(假设墙足够长),另三边用长为40米的木栏围成。
x
x
40-2x+2
注意:求含有二次项和一次项的代数式最值问题时,往往需考虑配方。
答:基地的最大面积为 平方米
通过这节课的学习活动你有哪些收获?
一元二次方程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用
方程两边都是整式
ax +bx+c=0(a 0)
只含有一个未知数
求知数的最高次数是2
配方法
公式法
开平方法
因式分解法
二次项系数为1,而一次项系数为偶数
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
