浙教版数学九年级上册 3.1 圆 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 3.1 圆 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 13:36:04 | ||
图片预览




文档简介
(共18张PPT)
3.1 圆(1)
圆是我们在日常生活中常见的几何图形
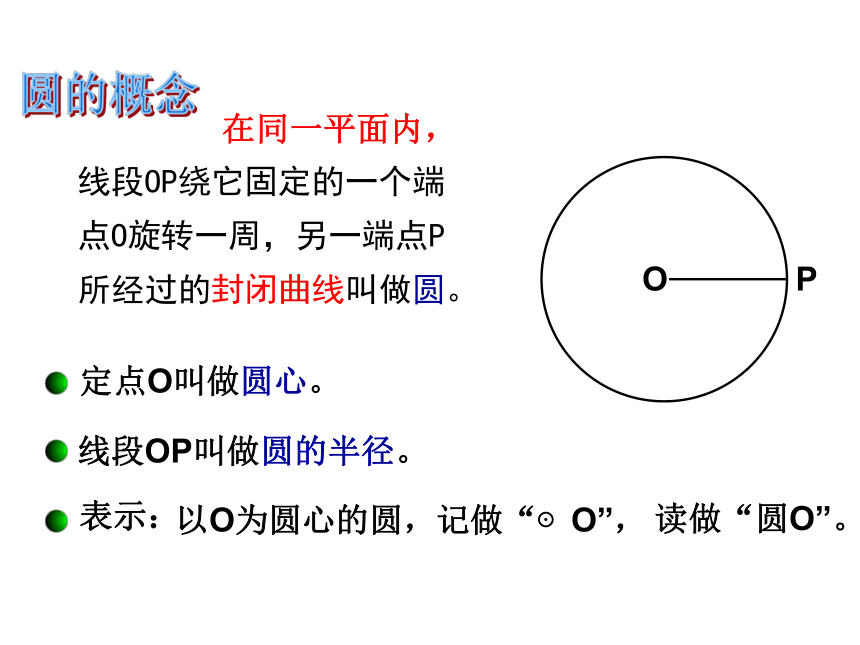
线段OP绕它固定的一个端点O旋转一周,另一端点P所经过的封闭曲线叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
O
P
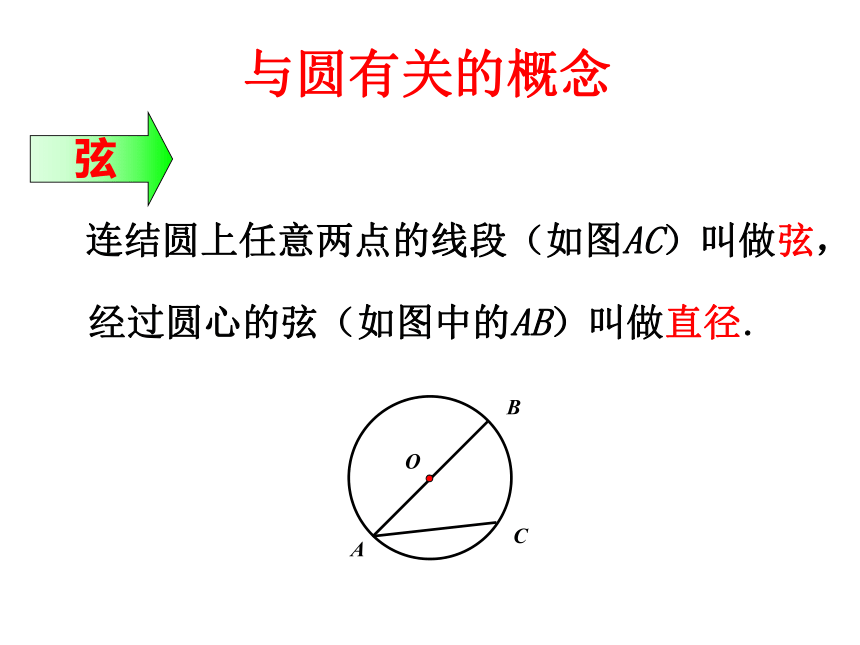
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连结圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
圆上任意两点间的部分叫做圆弧,简称弧.
以A、C为端点的弧记作 ,读作“弧AC ”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧
⌒
AC
与圆有关的概念
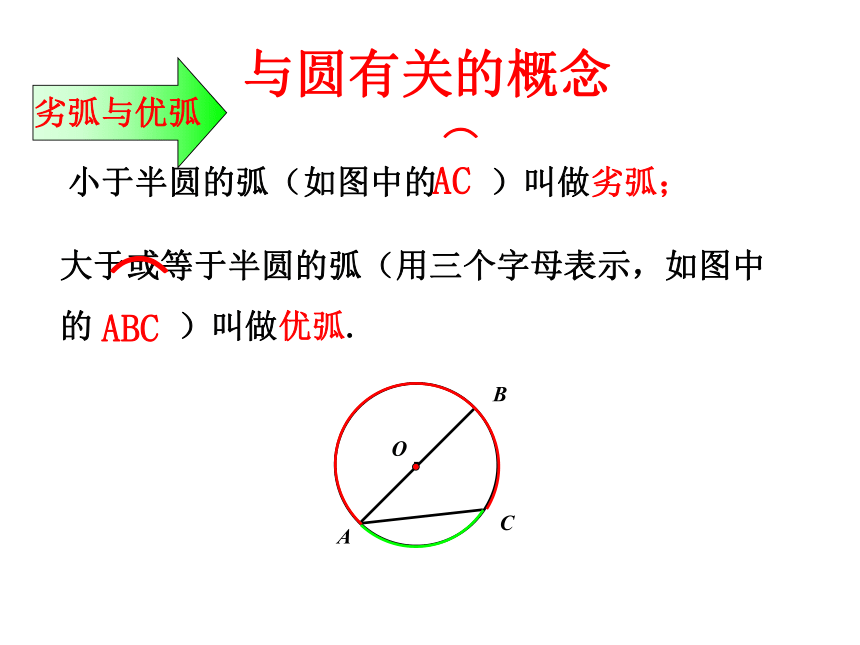
大于或等于半圆的弧(用三个字母表示,如图中
的 )叫做优弧.
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
⌒
⌒
ABC
AC
劣弧与优弧
与圆有关的概念
(1)请找出图中所有的弦;
(2)请任选一条弦,写出这条弦所对的弧;
练一练
1.看图回答
A
B
C
O
D
2、如图,请正确的方式表示出以点A为端点的优弧及劣弧.
劣弧:
优弧:
练一练
O1
r
O2
r
半径相等的两个圆叫做等圆
等圆
同心圆
等圆
圆心相同,半径不等
半径相等,圆心不同
与圆有关的概念
等弧
把能够重合的圆弧称为相等的弧
思考:长度相等的弧是不是等弧?
等弧的意义在于全等,而不是相等。
等弧在同圆或等圆中
与圆有关的概念
1、判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)直径是最长的弦;
(5)等弧就是拉直以后长度相等的弧。
·
O
判一判
2.下图是一个圆形靶的示意图,O为中心,小明向上面投了3支飞镖,它们分别落在了A、B、C点.
(1)这三个点与⊙O分别有怎样的位置关系?
(2)这三个点到圆心O的距离d与⊙O的半径r有怎样的数量关系
点A 在圆内,点B在圆上,点C 在圆外.
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d<r;
O
A
B
C
O
判一判
O
⊙O的半径为r,点到圆心的距离为d
B
A
C
d=r
d<r
d>r
点与圆的位置关系
已知点与圆的位置关系可以确定该点到圆心的距离d与半径r的关系,
d
d
r
反过来,已知点到圆心的距离d与半径r的关系可以确定该点与圆的位置关系。
圆内
圆上
圆外
已知⊙O的面积为25π
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
圆内
5
(作业题4)
练一练
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
关键是分别求出点B,C,D到点A的距离。
练题
E
变式:若BC是一条马路,且马路上有行人和车辆, 在爆破时也不能影响到马路的行人和车辆,那结果又如何呢?
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
练题
1、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
练一练
1、圆、弦和弧的概念及其表示方法;
小结:
2、同一平面内点与圆的位置关系及其判定。
3.1 圆(1)
圆是我们在日常生活中常见的几何图形
线段OP绕它固定的一个端点O旋转一周,另一端点P所经过的封闭曲线叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
O
P
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连结圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
圆上任意两点间的部分叫做圆弧,简称弧.
以A、C为端点的弧记作 ,读作“弧AC ”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧
⌒
AC
与圆有关的概念
大于或等于半圆的弧(用三个字母表示,如图中
的 )叫做优弧.
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
⌒
⌒
ABC
AC
劣弧与优弧
与圆有关的概念
(1)请找出图中所有的弦;
(2)请任选一条弦,写出这条弦所对的弧;
练一练
1.看图回答
A
B
C
O
D
2、如图,请正确的方式表示出以点A为端点的优弧及劣弧.
劣弧:
优弧:
练一练
O1
r
O2
r
半径相等的两个圆叫做等圆
等圆
同心圆
等圆
圆心相同,半径不等
半径相等,圆心不同
与圆有关的概念
等弧
把能够重合的圆弧称为相等的弧
思考:长度相等的弧是不是等弧?
等弧的意义在于全等,而不是相等。
等弧在同圆或等圆中
与圆有关的概念
1、判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)直径是最长的弦;
(5)等弧就是拉直以后长度相等的弧。
·
O
判一判
2.下图是一个圆形靶的示意图,O为中心,小明向上面投了3支飞镖,它们分别落在了A、B、C点.
(1)这三个点与⊙O分别有怎样的位置关系?
(2)这三个点到圆心O的距离d与⊙O的半径r有怎样的数量关系
点A 在圆内,点B在圆上,点C 在圆外.
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d<r;
O
A
B
C
O
判一判
O
⊙O的半径为r,点到圆心的距离为d
B
A
C
d=r
d<r
d>r
点与圆的位置关系
已知点与圆的位置关系可以确定该点到圆心的距离d与半径r的关系,
d
d
r
反过来,已知点到圆心的距离d与半径r的关系可以确定该点与圆的位置关系。
圆内
圆上
圆外
已知⊙O的面积为25π
(1)若PO=5.5,则点P在 ;
(2)若PO=4,则点P在 ;
(3)若PO= ,则点P在圆上。
圆外
圆内
5
(作业题4)
练一练
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
因施工需要,必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏,问爆破影响面的半径应控制在什么范围内?
关键是分别求出点B,C,D到点A的距离。
练题
E
变式:若BC是一条马路,且马路上有行人和车辆, 在爆破时也不能影响到马路的行人和车辆,那结果又如何呢?
例1 如图所示,在A地正北80m的B处有一幢民房,正西100m的C处有一变电设施,在BC的中点D处是一古建筑。
练题
1、如图,已知矩形ABCD
的边AB=3厘米,AD=4厘米。
(1)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(2)若以A点为圆心作圆A,使B、C、D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是什么?
练一练
1、圆、弦和弧的概念及其表示方法;
小结:
2、同一平面内点与圆的位置关系及其判定。
同课章节目录
