矩形复习[下学期]

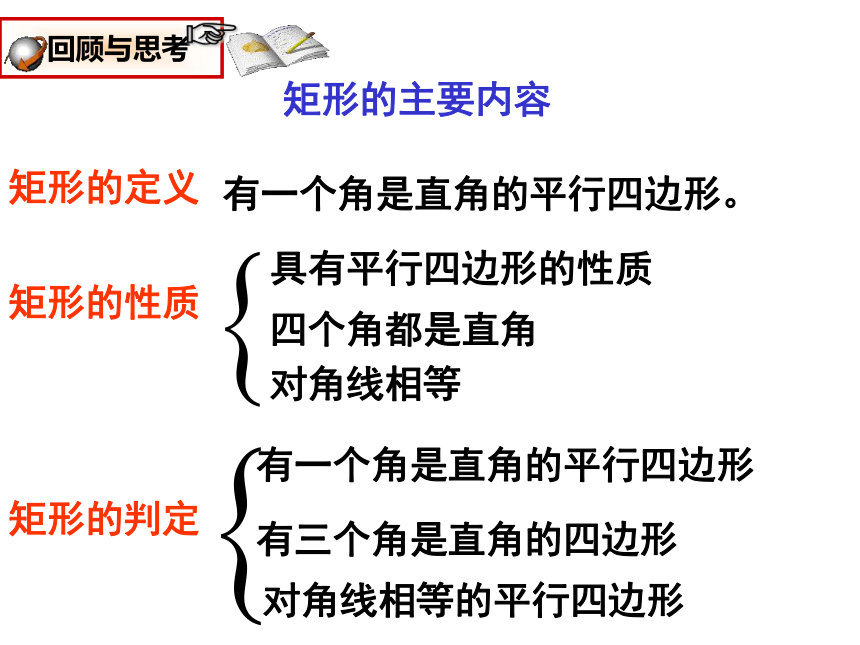
课件23张PPT。欢迎光临指导矩形复习课矩形的定义矩形的性质矩形的判定具有平行四边形的性质四个角都是直角对角线相等的平行四边形对角线相等有一个角是直角的平行四边形有三个角是直角的四边形矩形的主要内容有一个角是直角的平行四边形。直角三角形的性质30°一半中线一半1、在直角三角形中，______角所对的直角
边等于斜边的_______。
2、在直角三角形中，斜边上的______等于
斜边的______。 一位很有名望的木工师傅，招收了两名徒弟，
一天，师傅有事外出，两徒弟就自已在家练习用
两块四边形的废料各做了一扇矩形式的门，完事
之后，两人都说对方的门不是矩形，而自已 的是
矩形。
甲的理由是：“我用角尺量我的门任意三个角，
发现它们都是直角。所以我这个四边形门就是矩形”。
乙的理由是：“我用直尺量这个门的两条对角
线，发现它们的长度相等，所以我这个四边形门
就是矩形”。
根据它们的对话，你能肯定谁的门一定是矩形，
为什么？
谁正确？判断下列说法是否正确？⑴对角线相等的四边形是矩形 （ ）⑵对角线互相平分且相等的四边形是矩形( ）
⑶有一个角是直角的四边形是矩形（ ）
⑷有三个角是直角的四边形是矩形（ ）
⑸ 四个角都相等的四边形是矩形 （ ）
(6)对角线相等且互相垂直的四边形是矩形
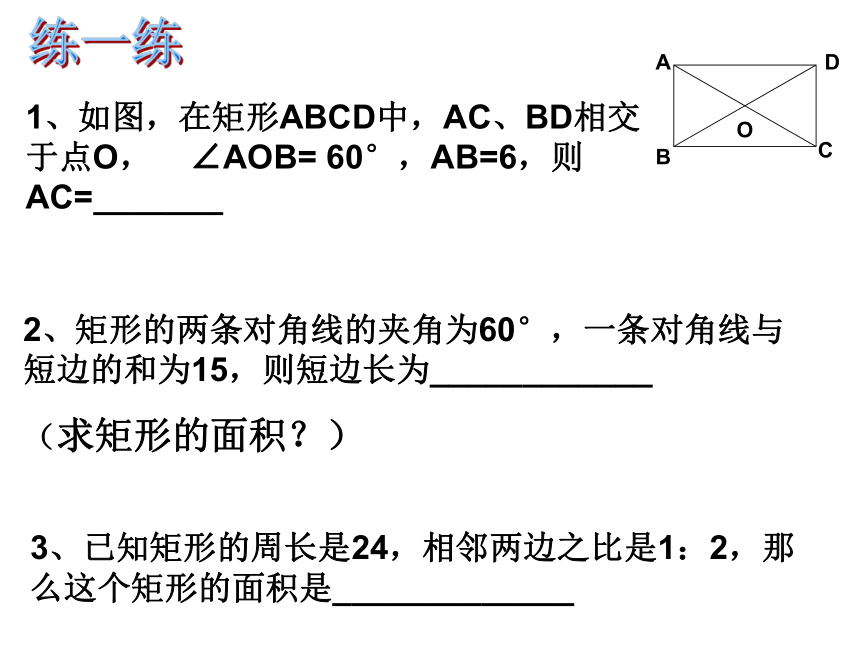
（ ）XXX√√√1、如图，在矩形ABCD中，AC、BD相交于点O， ∠AOB= 60°，AB=6，则AC=_______练一练3、已知矩形的周长是24，相邻两边之比是1：2，那么这个矩形的面积是_____________2、矩形的两条对角线的夹角为60°，一条对角线与短边的和为15，则短边长为____________
（求矩形的面积？）
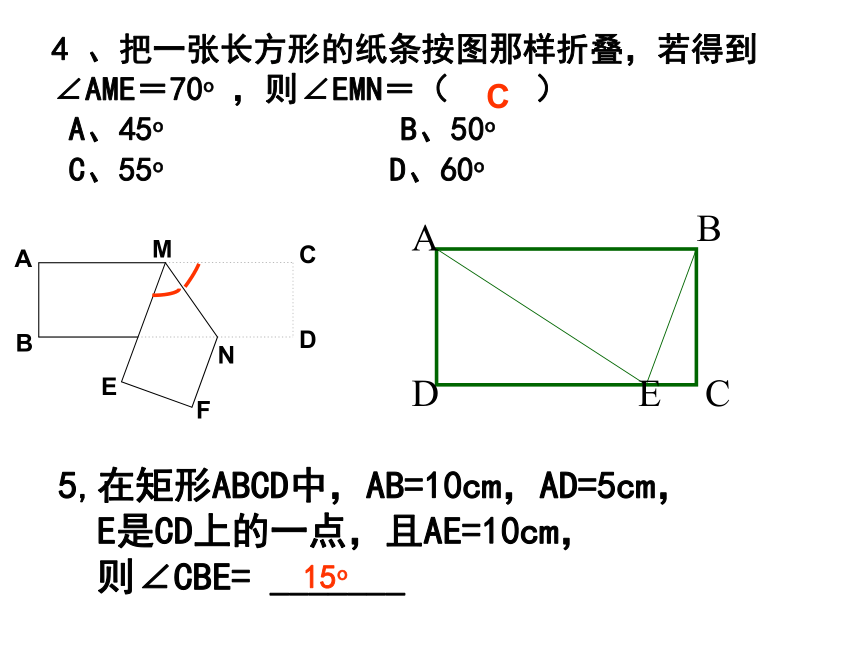
4 、把一张长方形的纸条按图那样折叠，若得到
∠AME＝70o ，则∠EMN＝（ ）
A、45o B、50o
C、55o D、60o C 5,在矩形ABCD中，AB=10cm，AD=5cm，
E是CD上的一点，且AE=10cm，
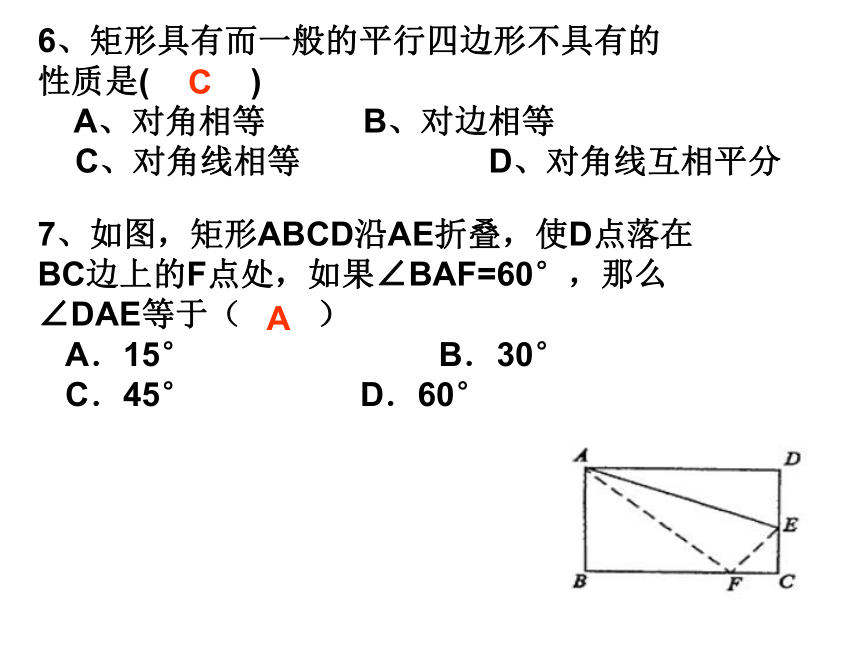
则∠CBE= _______15o6、矩形具有而一般的平行四边形不具有的
性质是(　　　)
A、对角相等 B、对边相等
C、对角线相等 D、对角线互相平分7、如图，矩形ABCD沿AE折叠，使D点落在
BC边上的F点处，如果∠BAF=60°，那么
∠DAE等于（ ）
A．15° B．30°
C．45° D．60° AC8．直角三角形斜边上的高和斜边上的中线分别是5cm和6cm，则它的面积是（ ）∵∠ACB=90ο,中线CD=6cm∴斜边AB=2CD=12（cm）∵CE⊥AB，CE=5cm∴△ABC的面积为:12×5÷2=30(cm2)9.矩形ABCD的两条对角线AC、BD相交于点O,AE垂直于BD于E，若∠DAE=3∠BAE，则∠EAC=？∴∠EAC=90ο－2×22.5ο=45ο解∵四边形ABCD是矩形∴OA=OD∴∠OAD=∠ODA∵∠DAE=3∠BAE ， ∠DAE+∠BAE=90ο∴∠BAE=22.5ο∴∠ADO=∠BAE=22.5ο1、已知如图矩形ABCD中AE⊥BD，BF⊥AC，
E、F分别为垂足，试说明AE=BF的理由。练习：已知□ ABCD的对角线AC、BD
相交于点O，ΔAOB是等边三角形，
你能说明这个平行四边形是矩形吗 ？变式练习：2、如图，M，N是 □ ABCD的对边AD,BC上的中点，且 AD=2AB。试说明四边形PMQN是矩形。小试牛刀3、如图，M，N是 □ ABCD的对边AD,BC上的中点，且 AD=2AB。试说明四边形PMQN是矩形。∵ AM=MD AD=2AB
∴ AB=AM
∴ ∠AMB=∠ABM∵ AD // BC
∴ ∠AMB=∠MBC
∴ ∠ABM=∠MBC同理 ∠ BAN=∠NAM ∵ ∠DAB+∠ABC=180o
∴ ∠NAB+∠ABM=90o
∴ ∠APB=∠MPN=90o
同理∠PNQ=∠NQM=90o∴四边形PMQN是矩形证明3,△ABC中，点O是AC边上的一个动点，过点O作直线M N∥BC，设M N交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F．(1)求证：EO=FO
(2)当点O运动到何处时，四边形AECF是矩形?并证明你的结论．(1)证明
∵ CE 平分∠ ACB
∴ ∠ ACE= ∠ ECB
∵ MN // BC
∴ ∠ ECB= ∠ OEC
∴ ∠ OEC= ∠ ECO
∴ OE=OC
同理OF=OC
∴ OE=OF(2)当O为AC的中点时,
四边形AECF是矩形
∵ OA=OC OE=OF
∴ 四边形AECN是平行四边形
∵ OE=OC=OF
∴ AC=EF
∴ 四边形AECN是矩形 4, 如图，矩形纸片ABCD中，AB=3厘米，BC=4厘米，现将A、C重合，使纸片折叠压平，
设折痕为EF。试确定重叠部分△AEF的面积。ABECDFG1、现有如图所示的方角铁皮,工人师傅想用一条直线将它分割成面积相等的两部分,请你帮助工人师傅设计三种不同的分割方案(保留作图痕迹).思考题2.用24根火柴棒首尾相接摆成一个矩形,你能吗?若能,最多能摆出几个?画图表示.若不能,请你说明理由.当矩形的长和宽分别为多少根火柴棒时,矩形的面积最大?思考题 3、田村有一口呈四边形的池塘，在它 的四个角A、B、C、D处均种有一棵大核桃树．田村准备开挖鱼池建养鱼苗，想使池塘面积扩大一倍，又想保持 核桃树不动，并要求扩建后的池塘成平行四边形形状， 请问田村能否实现这一设想?若能，请你设计并画出图形；若不能，请说明理 由．体会.分享 说能出你这节课的收获和体验
让大家与你分享吗？谢谢 再见