5.2不等式的基本性质[上学期]

课件15张PPT。5.2不等式的基本性质合作学习（1）已知a（不等式的传递性）(2)观察:用“<”或“>”填空,并找一找其中的规律.Ａ：5>3, 　 5+2____3+2 , 　　5－2____3－2 ;　Ｂ：　–1<3 , -1+2____3+2 , -1－3____3－3 ;
会发现:当不等式两边加或减去同一个数时,不等号的方向______
不变不变不变不等式性质2：不等式的两边都加上（或减去）同一个数，所得到的不等式仍成立。
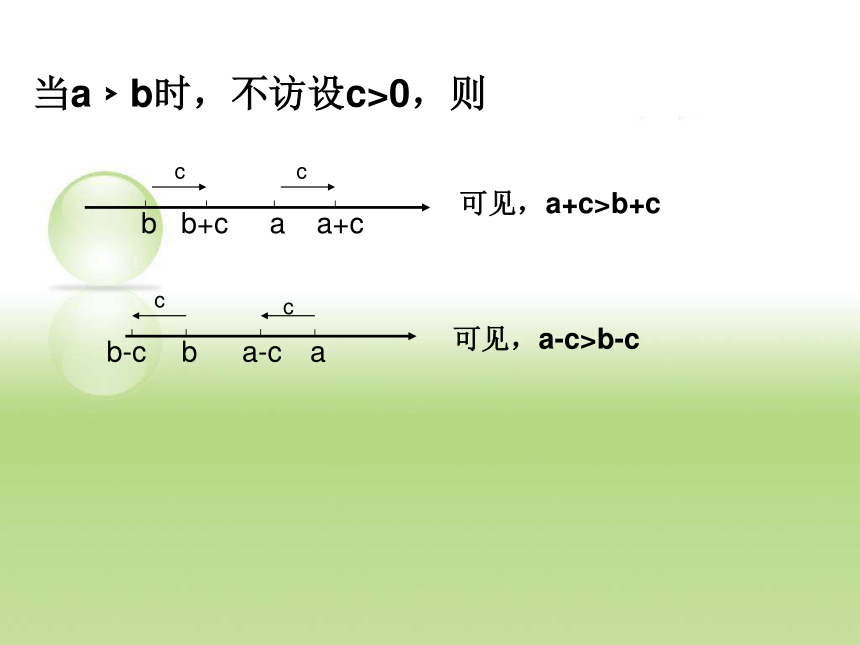
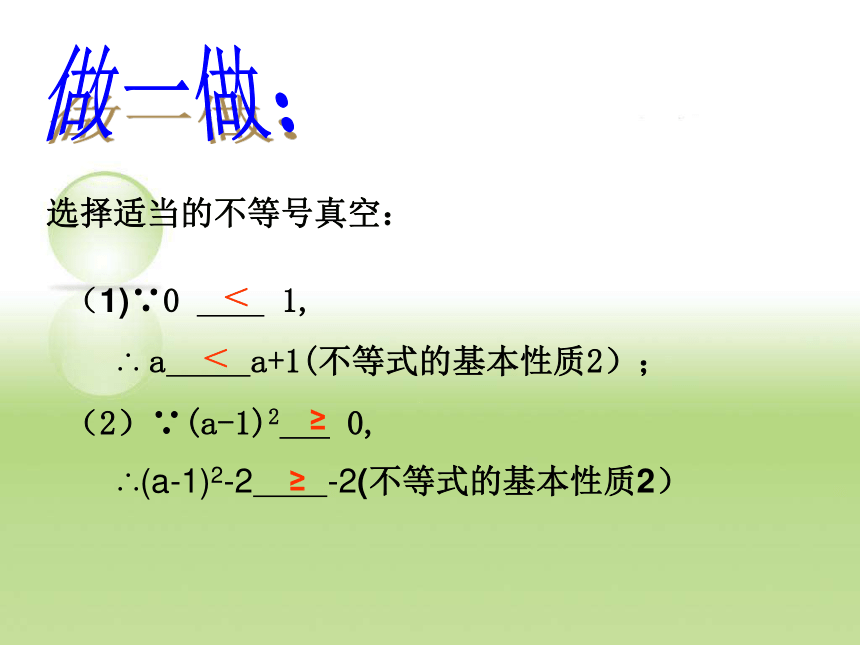
你能用数轴上点的位置关系说明这个性质吗？﹥﹥﹤﹤当a﹥b时，不访设c>0，则可见，a+c>b+c可见，a-c>b-c做一做：选择适当的不等号真空：（1)∵0 1,
　∴ a a+1(不等式的基本性质2）；
（2）∵(a-1)2 0,
　∴(a-1)2-2 -2(不等式的基本性质2）＜＜≥≥(３)观察:用“<”或“>”填空,并找一找其中的规律.Ａ：6＞2, 6×5____2×5 ,　 6×(-5)____2×(-5) ;
Ｂ：–2<3, 　(-2)×6____3×6 ,　 (-2)×(-6)____3×(-6)
Ｃ：6＞2, 6÷5____2÷5 ,　　 6÷ (-5)____2÷ (-5) ;Ｄ：–2<3, (-2) ÷6____3÷6 ,　 (-2) ÷(-6)____3÷ (-6)﹥﹥﹥﹥﹤﹤﹤﹤会发现：当不等式的两边同乘（或除以）同一个正数时,不等号的方向______;而乘（或除以）同一个负数时,不等号的方向______.
不变改变不等式的基本性质3: 不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.如果a＞b,且c＞0,那么ac＞bc, a÷c＞b÷c.
如果a＞b,且c＜0,那么ac＜bc, a÷c＜b÷c.
回顾不等式的基本性质：性质1：若a＜b，b＜c，则a＜c。
性质2：不等式的两边都加上(或减去)同一个数,所得到的
不等式仍成立.
如果a＞b,那么a+c＞b+c,a-c＞b-c.
如果a＜b,那么a+c＜b+c,a-c＜b-c.
性质3：不等式的两边都乘(或都除以)同一个正数,所得到
的不等式仍成立;不等式的两边都乘(或都除以)同
一个负数,必须把不等号的方向改变,所得到的不等式成立.
如果a＞b,且c＞0,那么ac＞bc, a÷c＞b÷c.
如果a＞b,且c＜0,那么ac＜bc, a÷c＜b÷c.
思考：1、若x+1＞0，两边同加上-1，得＿＿＿＿＿＿（依据什么？）
2、若2x＞-6，两边同除以2，得＿＿＿＿＿＿（依据什么？）
3、若-3x＜6，两边同除以-3，得＿＿＿＿＿＿（依据什么？）做一做：　　我国于2001年12月11日正式加入世界贸易组织（WTO）。加入前，产品A的进口税超过产品B的进口税的1倍以上；加入后，这两种产品的进口税都下调了15%。你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗？请说明理由。　 解　设加入前产品A，B的进口税分别为a美元,b美元。由题意,得,a>2b。加入后A，B两种产品的进口税分别为（1-15%）a，（1-15%）b，由不等式的基本性质3，
∵　1-15%＞0
∴（1-15%）a＞2 （1-15%）b
即表示产品A的进口税仍超过产品B的进口税的1倍以上。例　已知a<0 ，试比较2a与a的大小。解法一：∵2＞1，a＜0，
∴2a＜a（不等式的基本性质3）解法二：　在数轴上分别表示2a和a的点（a＜0），如图.2a位于a的左边，所以2a＜a想一想：还有其他比较2a与a的大小的方法吗？∵ 2a-a=a, 又∵ a＜0,
∴ 2a-a＜0,
∴2a2、若-a＜b，则a＿-b。
3、-a＞-b，则2-a＿2-b。
4、a＞0，且（1-b）a＜0，则b＿1。
5、若a＜b，b＜2a-1，则a＿2a-1＞＞＞＜＞想一想，说一说： 下列各题是否正确?请说明理由(1)如果a＞b,那么ac＞bc(2)如果a＞b,那么ac2 ＞bc2
(3)如果ac2＞bc2,那么a＞b(4)如果a＞b,那么a-b＞0(5)如果ax＞b且a≠0,那么x＞b/a
若x﹤y,且（a－3）x﹥(a－3)y,求a的取值范围。想一想:感悟与反思 通过这节课的学习活动你有哪些收获？