浙教版九年级上册 第三章《圆的基本性质》(3.1—3.4)检测(无答案)
文档属性
| 名称 | 浙教版九年级上册 第三章《圆的基本性质》(3.1—3.4)检测(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-08 09:00:46 | ||
图片预览

文档简介
九上《圆的基本性质》(3.1—3.4)检测卷
(总分:100分)
一、选择题(共6小题,每小题4分,共24分)
1.下列命题正确的是( ) (上课时一直在讲的知识点)
A.三点确定一个圆 B.圆有且只有一个内接三角形
C.三角形的外心是三角形三边中线的交点 D.矩形的四个顶点可以在同一个圆上
2.下列命题正确的是( ) (上课时一直在讲的知识点)
A.相等的弧所对的弦相等 B.相等的圆心角所对的弧相等
C.垂直弦的直线平分这条弦,且平分这条弦所对的弧
D.平分弦的直径垂直这条弦,且平分这条弦所对的弧
3.如图,☉O的直径长为10,弦AB的长为8,P是弦AB上一点,若OP的长是整数,则满足条件的点P有( ) (课堂内外A本第28页第10题)
A.3个 B.4个 C.5个 D.6个
4.如图,过☉O内点M的最长弦为34 cm,最短弦为16 cm,那么OM的长为( )
(课堂内外A本第27页第5题改变数字)
A.16 cm B.15 cm C.14 cm D.12 cm
5.如图,将半径为6cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
(课堂内外A本第27页第3题改变数字)
A.cm B.cm C.cm D.cm
6.在半径长为1的圆中,长为的弦所对的劣弧的度数为( )(上课时讲的拓展知识点)
A.36° B.61.8° C.108° D.135°
二、填空题(共6小题,每小题4分,共24分)
7.在平面直角坐标中,以坐标原点为圆心,4.8为半径长作圆,则点(3,4)在圆 .(填内、上或外)(课堂内外B本第21页第3题改变数字)
8.已知一个直角三角形的直角边长分别是1和2,则该直角三角形的外接圆半径长为 .
(课堂内外A本第25页第3题改变数字)
9.在☉O中,弦AB垂直平分半径OC,则弦AB所对弧的度数为 .
(课堂内外B本第21页第8题)
10.已知一个弓形的弦长为8 dm,弓高也为8 dm,则该弓形所在圆的半径长为 dm.
(课堂内外A本第29页第5题改变数字)
11.已知☉O的半径长为1,弦AB、AC的长分别为1和,则∠BAC的度数为 .
(上课时讲的拓展知识点)
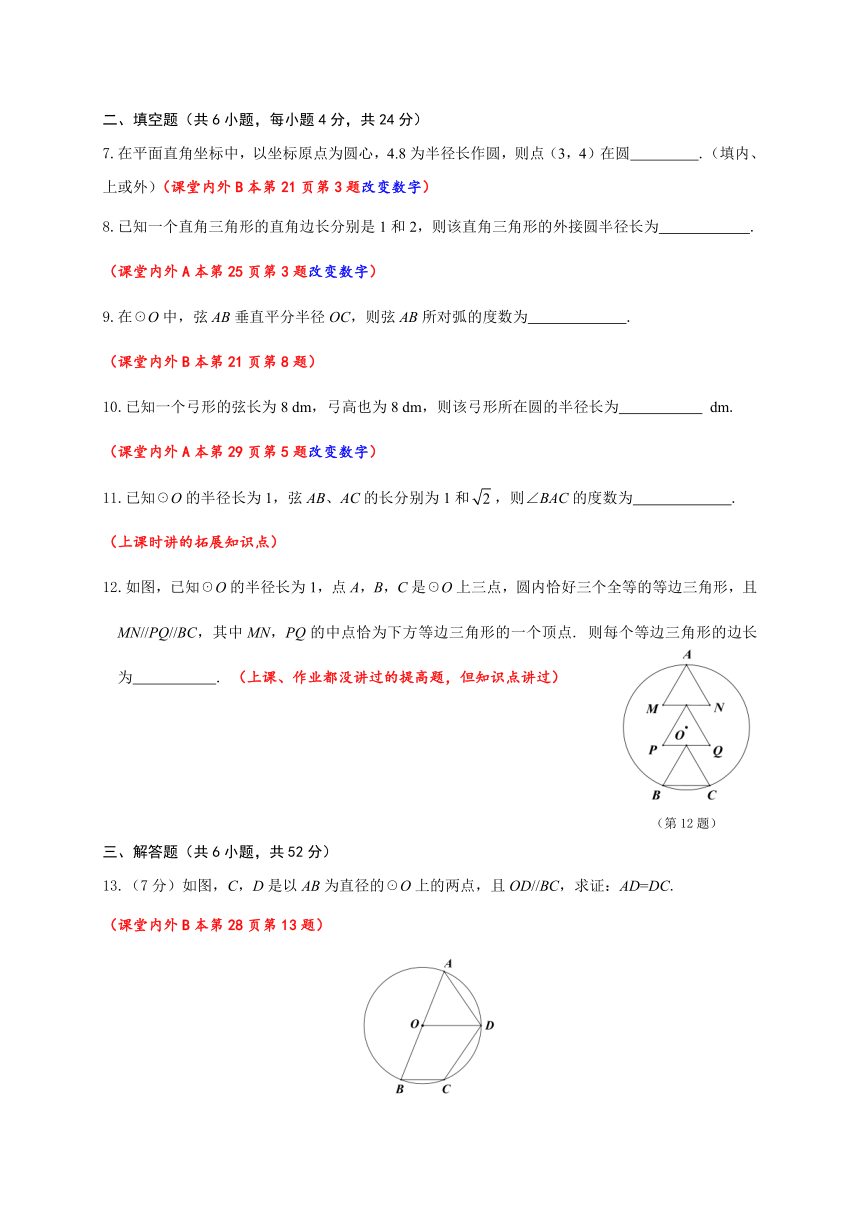
12.如图,已知☉O的半径长为1,点A,B,C是☉O上三点,圆内恰好三个全等的等边三角形,且MN//PQ//BC,其中MN,PQ的中点恰为下方等边三角形的一个顶点. 则每个等边三角形的边长为 . (上课、作业都没讲过的提高题,但知识点讲过)
三、解答题(共6小题,共52分)
13.(7分)如图,C,D是以AB为直径的☉O上的两点,且OD//BC,求证:AD=DC.
(课堂内外B本第28页第13题)
14.(7分)如图,☉O是△ABC的外接圆,且,,求☉O的半径长.
(课堂内外B本第26页第13题)
15.(7分)如图,☉O的弦AB,CD在圆内交于点P,连结PO,且PO恰好平分∠BPD,求证:AB=CD.
(课堂内外A本第30页第10题改编题)
16.(7分)如图,某地有一座圆弧形拱桥,桥下水面AB跨度为7.2米,记圆心为O,半径OC⊥AB于点D,测得CD的长为2.4米. 现有一艘宽3米、船舱顶部为矩形并高出水面2米的货船要经过拱桥,此货船能否顺利地通过这座桥?请通过计算说明.
(课堂内外A本第28页第17题)
17.(8分)如图,MN为半圆O的直径,半径OA⊥MN,D为OA的中点,过点D作BC//MN.
(1)判断四边形ABOC的形状,并说明理由;
(2).
(课堂内外A本第32页第15题)
18.(6分)如图,已知AB,CD,AD,BC是的四条弦,若,求证:.
(上课讲过的题型)
19.(10分)利用工具(圆规或直角三角尺)作图:
(1)找到这个圆的圆心O.
(2)找到△ABC旋转到△的旋转中心P.
(上课讲过的题型)
(总分:100分)
一、选择题(共6小题,每小题4分,共24分)
1.下列命题正确的是( ) (上课时一直在讲的知识点)
A.三点确定一个圆 B.圆有且只有一个内接三角形
C.三角形的外心是三角形三边中线的交点 D.矩形的四个顶点可以在同一个圆上
2.下列命题正确的是( ) (上课时一直在讲的知识点)
A.相等的弧所对的弦相等 B.相等的圆心角所对的弧相等
C.垂直弦的直线平分这条弦,且平分这条弦所对的弧
D.平分弦的直径垂直这条弦,且平分这条弦所对的弧
3.如图,☉O的直径长为10,弦AB的长为8,P是弦AB上一点,若OP的长是整数,则满足条件的点P有( ) (课堂内外A本第28页第10题)
A.3个 B.4个 C.5个 D.6个
4.如图,过☉O内点M的最长弦为34 cm,最短弦为16 cm,那么OM的长为( )
(课堂内外A本第27页第5题改变数字)
A.16 cm B.15 cm C.14 cm D.12 cm
5.如图,将半径为6cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为( )
(课堂内外A本第27页第3题改变数字)
A.cm B.cm C.cm D.cm
6.在半径长为1的圆中,长为的弦所对的劣弧的度数为( )(上课时讲的拓展知识点)
A.36° B.61.8° C.108° D.135°
二、填空题(共6小题,每小题4分,共24分)
7.在平面直角坐标中,以坐标原点为圆心,4.8为半径长作圆,则点(3,4)在圆 .(填内、上或外)(课堂内外B本第21页第3题改变数字)
8.已知一个直角三角形的直角边长分别是1和2,则该直角三角形的外接圆半径长为 .
(课堂内外A本第25页第3题改变数字)
9.在☉O中,弦AB垂直平分半径OC,则弦AB所对弧的度数为 .
(课堂内外B本第21页第8题)
10.已知一个弓形的弦长为8 dm,弓高也为8 dm,则该弓形所在圆的半径长为 dm.
(课堂内外A本第29页第5题改变数字)
11.已知☉O的半径长为1,弦AB、AC的长分别为1和,则∠BAC的度数为 .
(上课时讲的拓展知识点)
12.如图,已知☉O的半径长为1,点A,B,C是☉O上三点,圆内恰好三个全等的等边三角形,且MN//PQ//BC,其中MN,PQ的中点恰为下方等边三角形的一个顶点. 则每个等边三角形的边长为 . (上课、作业都没讲过的提高题,但知识点讲过)
三、解答题(共6小题,共52分)
13.(7分)如图,C,D是以AB为直径的☉O上的两点,且OD//BC,求证:AD=DC.
(课堂内外B本第28页第13题)
14.(7分)如图,☉O是△ABC的外接圆,且,,求☉O的半径长.
(课堂内外B本第26页第13题)
15.(7分)如图,☉O的弦AB,CD在圆内交于点P,连结PO,且PO恰好平分∠BPD,求证:AB=CD.
(课堂内外A本第30页第10题改编题)
16.(7分)如图,某地有一座圆弧形拱桥,桥下水面AB跨度为7.2米,记圆心为O,半径OC⊥AB于点D,测得CD的长为2.4米. 现有一艘宽3米、船舱顶部为矩形并高出水面2米的货船要经过拱桥,此货船能否顺利地通过这座桥?请通过计算说明.
(课堂内外A本第28页第17题)
17.(8分)如图,MN为半圆O的直径,半径OA⊥MN,D为OA的中点,过点D作BC//MN.
(1)判断四边形ABOC的形状,并说明理由;
(2).
(课堂内外A本第32页第15题)
18.(6分)如图,已知AB,CD,AD,BC是的四条弦,若,求证:.
(上课讲过的题型)
19.(10分)利用工具(圆规或直角三角尺)作图:
(1)找到这个圆的圆心O.
(2)找到△ABC旋转到△的旋转中心P.
(上课讲过的题型)
同课章节目录
