浙教版八年级上册 1.5 全等三角形判定(1)课件 15张PPT
文档属性
| 名称 | 浙教版八年级上册 1.5 全等三角形判定(1)课件 15张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 11:55:15 | ||
图片预览




文档简介
(共15张PPT)
全等三角形的判定(1)
年 级:八年级
学 科:数学(浙教版)
复习回顾
全等三角形
定义
A
B
C
D
E
F
能够重合的两个三角形
全等三角形
性质
∵ △ABC ≌△DEF
∴ AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形
判定
思考1:是否一定要满足三边相等,三个角相等,才能保证两个三角形全等吗?
思考2:能否在上述六个条件中选择部分条件,简捷的判断两个三角形全等?
探究新知
探究1 先画出一个△ABC,再画一个△DEF,使△ABC和△DEF满足上述条件中的一个(一边或一角相等)或两个(两边、一边一角或两角分别相等)。你画出的△ABC和△DEF一定全等吗?
满足上述六个条件中的一个或者两个,△ABC和△DEF不一定全等。满足上述条件中的三个,能保证△ABC和△DEF全等吗?
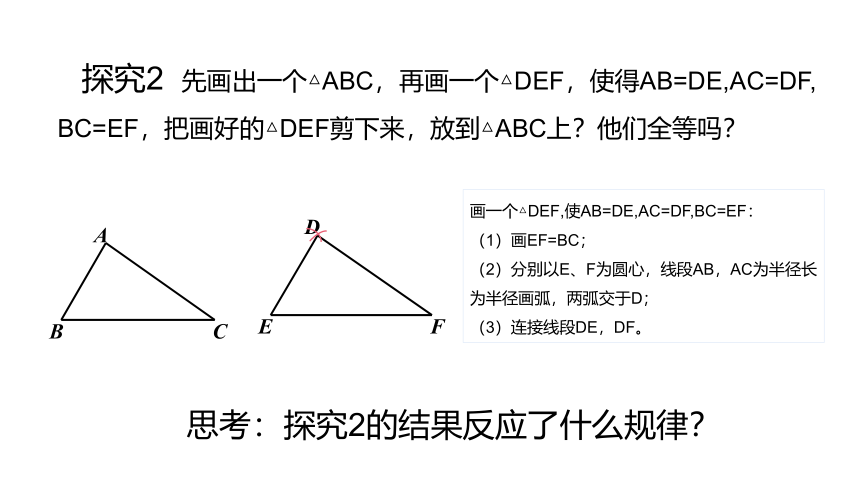
探究2 先画出一个△ABC,再画一个△DEF,使得AB=DE,AC=DF,
BC=EF,把画好的△DEF剪下来,放到△ABC上?他们全等吗?
A
B
C
D
E
F
画一个△DEF,使AB=DE,AC=DF,BC=EF:
(1)画EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径长为半径画弧,两弧交于D;
(3)连接线段DE,DF。
思考:探究2的结果反应了什么规律?
归纳总结
A
B
C
D
E
F
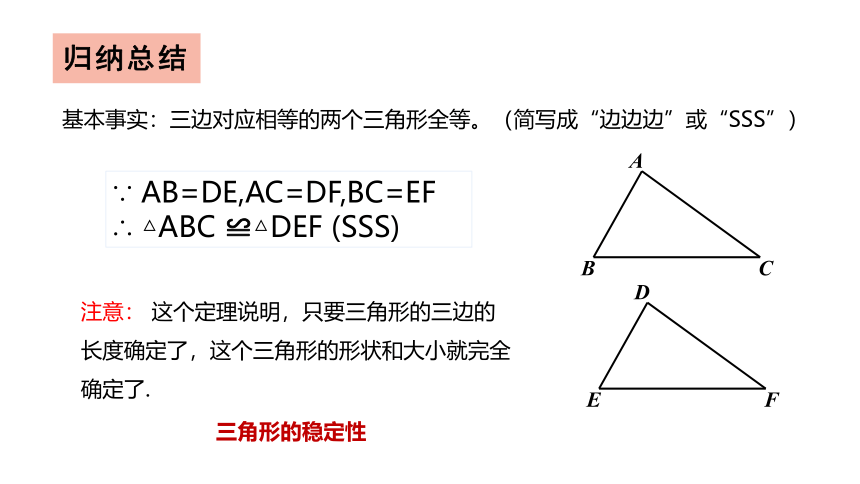
注意: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了.
基本事实:三边对应相等的两个三角形全等。(简写成“边边边”或“SSS”)
∵ AB=DE,AC=DF,BC=EF
∴ △ABC ≌△DEF (SSS)
三角形的稳定性
新知讲解
三角形的稳定性在生产和日常生活中有广泛的应用.
例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
典例精讲
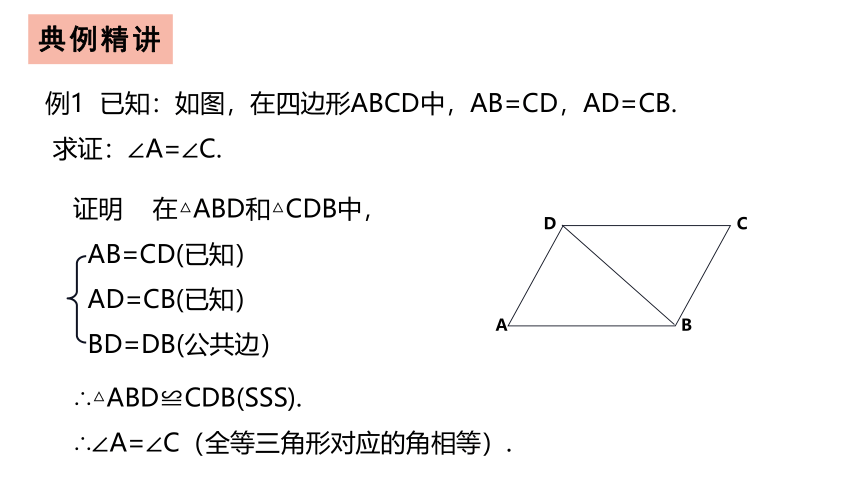
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
证明 在△ABD和△CDB中,
AB=CD(已知)
AD=CB(已知)
BD=DB(公共边)
A
B
C
D
∴△ABD≌CDB(SSS).
∴∠A=∠C(全等三角形对应的角相等).
A
B
C
D
E
F
如图,点A、F、D、E在同一条直线上,且AB=EC,BD=CF,AF=ED. 求证:∠A=∠E.
变式练习
证明 ∵AF=ED(已知)
∴AF+DF=ED+DF,即AD=EF
在△ABD和△CDB中,
AB=EC(已知)
BD=CF(已知)
AD=CB
∴△ABD≌CEF(SSS)
∴∠A=∠E.
新知讲解
例2 已知∠BAC,用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
(1)在∠ABC的两边AB和AC上分别截取AE,AF,使AE=AF.
B
A
C
F
E
(2)分别以E,F为圆心,以大于 EF的长为半径作弧,两弧在∠BAC内交于点D.
B
A
C
F
E
D
(3)作射线AD.则AD是∠BAC的平分线.
B
A
C
F
E
D
事实上,如图,连结DE,DF.
由作法可得△ADF≌△ADE,
∴∠1=∠2(全等三角形的对应角相等)
即AD平分∠BAC.
B
A
C
F
E
D
1
2
知识总结
1.三角形全等的判定
(边边边)
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
判定
思路分析
书写规范
结合图形找隐含条件和现有条件,证准备条件
2.三角形具有稳定性
课堂练习
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A.30° B.50° C.60° D.100°
3.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.AD=CF
C.BC∥EF D.DC=CF
D
B
课堂练习
4.如图,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
(2)∵∠A=55°,∠B=88°,
∴∠ACB=180°-∠A-∠B
=180°-55°-88°=37°.
又∵△ABC≌△DEF,
∴∠F=∠ACB=37°
(1)证明 ∵AD=CF(已知)
∴AD+CD=CF+DC,即AC=DF
在△ABC和△DEF中,
AB=DE(已知)
BC=EF(已知)
AC=DF
∴△ABC≌DEF(SSS)
课堂练习
作业布置
(1)完成作业本
(2)书本P27-28作业题
谢谢聆听!
全等三角形的判定(1)
年 级:八年级
学 科:数学(浙教版)
复习回顾
全等三角形
定义
A
B
C
D
E
F
能够重合的两个三角形
全等三角形
性质
∵ △ABC ≌△DEF
∴ AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形
判定
思考1:是否一定要满足三边相等,三个角相等,才能保证两个三角形全等吗?
思考2:能否在上述六个条件中选择部分条件,简捷的判断两个三角形全等?
探究新知
探究1 先画出一个△ABC,再画一个△DEF,使△ABC和△DEF满足上述条件中的一个(一边或一角相等)或两个(两边、一边一角或两角分别相等)。你画出的△ABC和△DEF一定全等吗?
满足上述六个条件中的一个或者两个,△ABC和△DEF不一定全等。满足上述条件中的三个,能保证△ABC和△DEF全等吗?
探究2 先画出一个△ABC,再画一个△DEF,使得AB=DE,AC=DF,
BC=EF,把画好的△DEF剪下来,放到△ABC上?他们全等吗?
A
B
C
D
E
F
画一个△DEF,使AB=DE,AC=DF,BC=EF:
(1)画EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径长为半径画弧,两弧交于D;
(3)连接线段DE,DF。
思考:探究2的结果反应了什么规律?
归纳总结
A
B
C
D
E
F
注意: 这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了.
基本事实:三边对应相等的两个三角形全等。(简写成“边边边”或“SSS”)
∵ AB=DE,AC=DF,BC=EF
∴ △ABC ≌△DEF (SSS)
三角形的稳定性
新知讲解
三角形的稳定性在生产和日常生活中有广泛的应用.
例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
典例精讲
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
证明 在△ABD和△CDB中,
AB=CD(已知)
AD=CB(已知)
BD=DB(公共边)
A
B
C
D
∴△ABD≌CDB(SSS).
∴∠A=∠C(全等三角形对应的角相等).
A
B
C
D
E
F
如图,点A、F、D、E在同一条直线上,且AB=EC,BD=CF,AF=ED. 求证:∠A=∠E.
变式练习
证明 ∵AF=ED(已知)
∴AF+DF=ED+DF,即AD=EF
在△ABD和△CDB中,
AB=EC(已知)
BD=CF(已知)
AD=CB
∴△ABD≌CEF(SSS)
∴∠A=∠E.
新知讲解
例2 已知∠BAC,用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
(1)在∠ABC的两边AB和AC上分别截取AE,AF,使AE=AF.
B
A
C
F
E
(2)分别以E,F为圆心,以大于 EF的长为半径作弧,两弧在∠BAC内交于点D.
B
A
C
F
E
D
(3)作射线AD.则AD是∠BAC的平分线.
B
A
C
F
E
D
事实上,如图,连结DE,DF.
由作法可得△ADF≌△ADE,
∴∠1=∠2(全等三角形的对应角相等)
即AD平分∠BAC.
B
A
C
F
E
D
1
2
知识总结
1.三角形全等的判定
(边边边)
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
判定
思路分析
书写规范
结合图形找隐含条件和现有条件,证准备条件
2.三角形具有稳定性
课堂练习
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,AB=DE,AC=DF,BC=EF,则∠D等于( )
A.30° B.50° C.60° D.100°
3.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.AD=CF
C.BC∥EF D.DC=CF
D
B
课堂练习
4.如图,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
(2)∵∠A=55°,∠B=88°,
∴∠ACB=180°-∠A-∠B
=180°-55°-88°=37°.
又∵△ABC≌△DEF,
∴∠F=∠ACB=37°
(1)证明 ∵AD=CF(已知)
∴AD+CD=CF+DC,即AC=DF
在△ABC和△DEF中,
AB=DE(已知)
BC=EF(已知)
AC=DF
∴△ABC≌DEF(SSS)
课堂练习
作业布置
(1)完成作业本
(2)书本P27-28作业题
谢谢聆听!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
