浙教版数学九年级下册2.3三角形的内切圆 课件 (共17张PPT)
文档属性
| 名称 | 浙教版数学九年级下册2.3三角形的内切圆 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-13 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
2.3 三角形的内切圆
学习目标
1. 通过作图和探索,体验并理解三角形内切圆的性质;2. 通过作图操作,经历三角形内切圆的产生过程;3. 类比三角形内切圆与三角形外接圆,进一 步理解三角形内心和外心所具有的性质.
新知导入
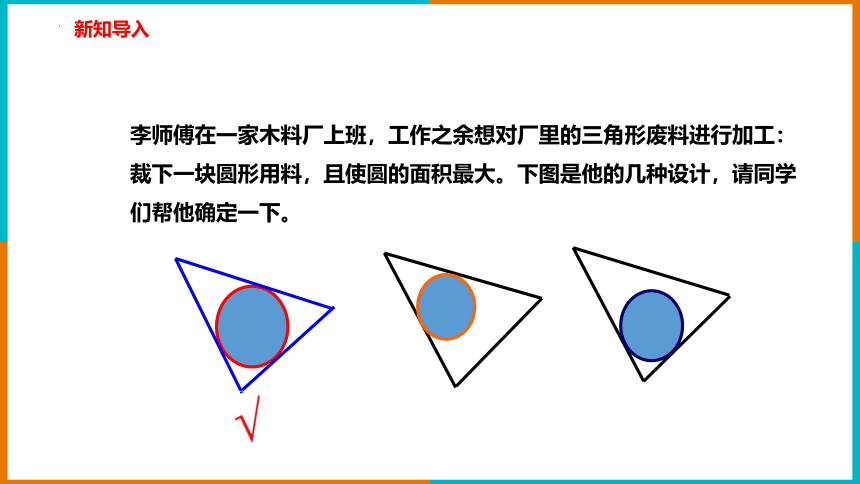
李师傅在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。下图是他的几种设计,请同学们帮他确定一下。
√
新知讲解
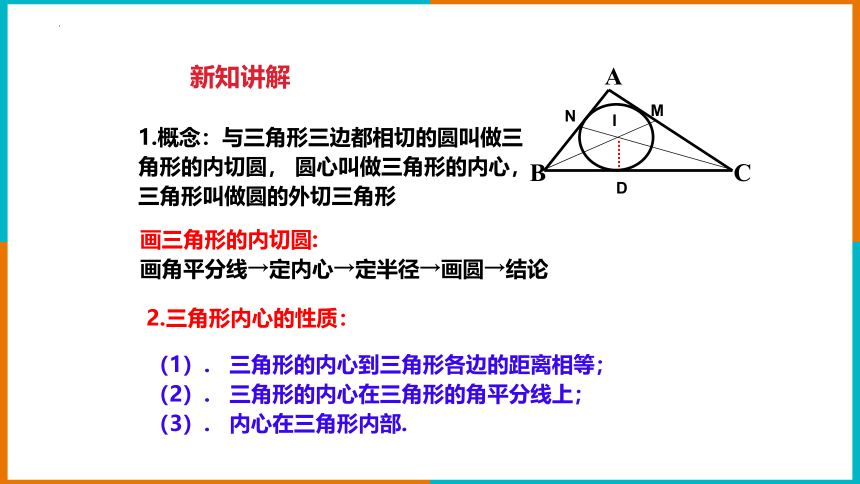
1.概念:与三角形三边都相切的圆叫做三角形的内切圆, 圆心叫做三角形的内心,
三角形叫做圆的外切三角形
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
2.三角形内心的性质:
(1). 三角形的内心到三角形各边的距离相等;
(2). 三角形的内心在三角形的角平分线上;
(3). 内心在三角形内部.
A
B
C
D
M
I
N
新知讲解
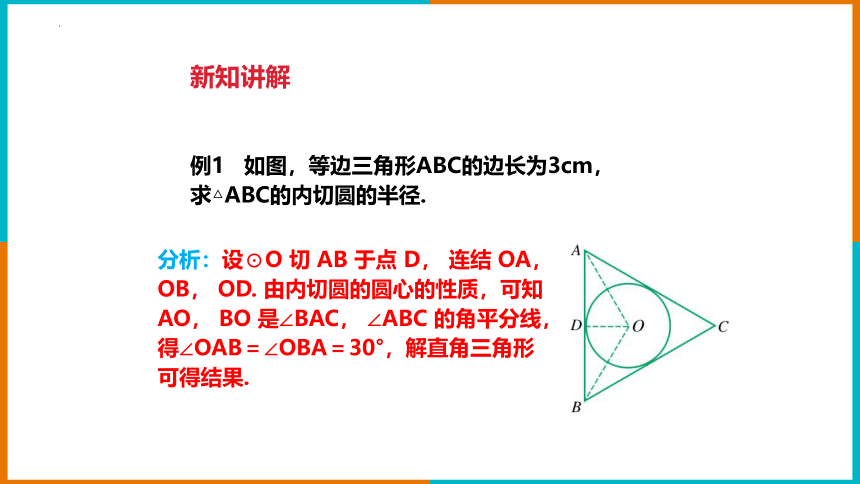
例1 如图,等边三角形ABC的边长为3cm, 求△ABC的内切圆的半径.
分析:设⊙O 切 AB 于点 D, 连结 OA, OB, OD. 由内切圆的圆心的性质,可知AO, BO 是∠BAC, ∠ABC 的角平分线,得∠OAB=∠OBA=30°,解直角三角形可得结果.
新知讲解
解 如图 , 设⊙O 切 AB 于点 D, 连结 OA, OB, OD.
∵ ⊙O 是△ABC 的内切圆,
∴AO, BO 是∠BAC, ∠ABC 的角平分线,
∵ △ABC 是等边三角形,
∴ ∠OAB=∠OBA=30°
∵OD⊥AB, AB=3cm,
∴ AD=BD= AB=1.5 (cm) ,
∴OD=ADtan 30 ° = (cm)
答: △ABC 的内切圆的半径为 cm
新知讲解
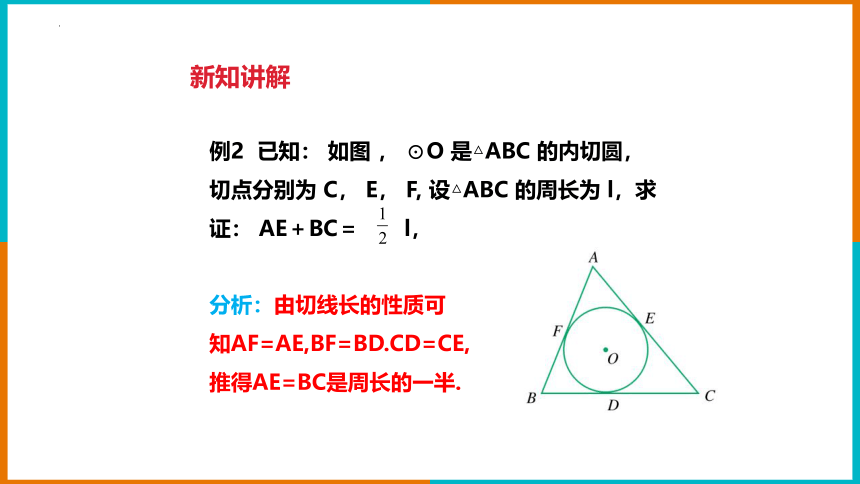
例2 已知: 如图 , ⊙O 是△ABC 的内切圆, 切点分别为 C, E, F, 设△ABC 的周长为 l,求证: AE+BC= l,
分析:由切线长的性质可知AF=AE,BF=BD.CD=CE,推得AE=BC是周长的一半.
新知讲解
证明 ∵ ⊙O 是△ABC的内切圆, E, F 为切点,
∴ AE=AF(切线长定理) .
同理, BD=BF, CD=CE,
∴ AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
= l
新知讲解
例3 已知:点I是△ABC的内心,AI交BC于D,交外接圆于E.求证:EB=EI=EC
A
B
C
I
D
E
1
2
3
4
5
分析:内切圆的圆心也叫三角形的内心,即三角形内角平分线的交点,由角平分线的性质,可得结果.
新知讲解
证明: 连结BI
∵I是△ABC的内心
∴∠3=∠4
∵ ∠ 1= ∠ 2, ∠ 2= ∠ 5
∴ ∠ 1= ∠ 5
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
A
B
C
I
D
E
1
2
3
4
5
新知讲解
注意
1. 任何一个三角形可作一个内切圆,内心都在三角形的内部; 在以后解有关正多边形的问题时,常常要用到这些性质.
2.三角形的内切圆中,切点与圆心的连线既是圆的半径,又垂直于边,同时三角形的边长可利用切线长定理,还可利用面积公式在三角形的三边与内切圆半径之间建直角三角形.
巩固提升
1、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130°
B
分析:先根据三角形的内角和定理求得∠B,再由切线的性质得∠BDO=∠BEO=90°,从而得出∠DOE.
巩固提升
2.如图, ⊙O是△ABC的内切圆,则点O 是 的( )
A.三条边的垂直平分线的交点
B.三角形平分线的交点
C. 三条中线的交点
D.三条高的交点
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,故选B.
B
巩固提升
3.如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
A.114° B.122° C.123° D.132°
D
分析:根据三角形内角和定理求出∠ABC+∠ACB,根据内心的概念得到2∠IBC=∠ABC,2∠ICB=∠ACB,根据三角形内角和定理计算即可.
拓展提升
【分析】首先证明四边形CFOE是正方形,设⊙O的半径为r,根据平行证明△OED∽△ACD,列比例式代入即可求解
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径是( )
A.1 B.1.5 C.2 D.2.5
拓展提升
解:∵⊙O是Rt△ABC的内切囫,
∴OE 丄 BC,OF 丄 AC,
∴∠OFC=∠OEC=90°
∵∠ACB=90°,
∴四边形CFOE是矩形,
∵OE=OF,
∴矩形CFOE是正方形,
∴OF=EC,
拓展提升
设⊙O的半径为 r,则 DE=CD-CE=2-r,OE=r,
∵OE//AC,
∴△OED∽△ACD,
∴r=1.5,
故选B
2.3 三角形的内切圆
学习目标
1. 通过作图和探索,体验并理解三角形内切圆的性质;2. 通过作图操作,经历三角形内切圆的产生过程;3. 类比三角形内切圆与三角形外接圆,进一 步理解三角形内心和外心所具有的性质.
新知导入
李师傅在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。下图是他的几种设计,请同学们帮他确定一下。
√
新知讲解
1.概念:与三角形三边都相切的圆叫做三角形的内切圆, 圆心叫做三角形的内心,
三角形叫做圆的外切三角形
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
2.三角形内心的性质:
(1). 三角形的内心到三角形各边的距离相等;
(2). 三角形的内心在三角形的角平分线上;
(3). 内心在三角形内部.
A
B
C
D
M
I
N
新知讲解
例1 如图,等边三角形ABC的边长为3cm, 求△ABC的内切圆的半径.
分析:设⊙O 切 AB 于点 D, 连结 OA, OB, OD. 由内切圆的圆心的性质,可知AO, BO 是∠BAC, ∠ABC 的角平分线,得∠OAB=∠OBA=30°,解直角三角形可得结果.
新知讲解
解 如图 , 设⊙O 切 AB 于点 D, 连结 OA, OB, OD.
∵ ⊙O 是△ABC 的内切圆,
∴AO, BO 是∠BAC, ∠ABC 的角平分线,
∵ △ABC 是等边三角形,
∴ ∠OAB=∠OBA=30°
∵OD⊥AB, AB=3cm,
∴ AD=BD= AB=1.5 (cm) ,
∴OD=ADtan 30 ° = (cm)
答: △ABC 的内切圆的半径为 cm
新知讲解
例2 已知: 如图 , ⊙O 是△ABC 的内切圆, 切点分别为 C, E, F, 设△ABC 的周长为 l,求证: AE+BC= l,
分析:由切线长的性质可知AF=AE,BF=BD.CD=CE,推得AE=BC是周长的一半.
新知讲解
证明 ∵ ⊙O 是△ABC的内切圆, E, F 为切点,
∴ AE=AF(切线长定理) .
同理, BD=BF, CD=CE,
∴ AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
= l
新知讲解
例3 已知:点I是△ABC的内心,AI交BC于D,交外接圆于E.求证:EB=EI=EC
A
B
C
I
D
E
1
2
3
4
5
分析:内切圆的圆心也叫三角形的内心,即三角形内角平分线的交点,由角平分线的性质,可得结果.
新知讲解
证明: 连结BI
∵I是△ABC的内心
∴∠3=∠4
∵ ∠ 1= ∠ 2, ∠ 2= ∠ 5
∴ ∠ 1= ∠ 5
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
A
B
C
I
D
E
1
2
3
4
5
新知讲解
注意
1. 任何一个三角形可作一个内切圆,内心都在三角形的内部; 在以后解有关正多边形的问题时,常常要用到这些性质.
2.三角形的内切圆中,切点与圆心的连线既是圆的半径,又垂直于边,同时三角形的边长可利用切线长定理,还可利用面积公式在三角形的三边与内切圆半径之间建直角三角形.
巩固提升
1、如图,⊙O是△ABC的内切圆,D、E、F是切点,∠A=50°,∠C=60°,则∠DOE=( )
(A)70° (B)110°
(C)120° (D)130°
B
分析:先根据三角形的内角和定理求得∠B,再由切线的性质得∠BDO=∠BEO=90°,从而得出∠DOE.
巩固提升
2.如图, ⊙O是△ABC的内切圆,则点O 是 的( )
A.三条边的垂直平分线的交点
B.三角形平分线的交点
C. 三条中线的交点
D.三条高的交点
解:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,故选B.
B
巩固提升
3.如图,在△ABC中,∠A=66°,点I是内心,则∠BIC的大小为( )
A.114° B.122° C.123° D.132°
D
分析:根据三角形内角和定理求出∠ABC+∠ACB,根据内心的概念得到2∠IBC=∠ABC,2∠ICB=∠ACB,根据三角形内角和定理计算即可.
拓展提升
【分析】首先证明四边形CFOE是正方形,设⊙O的半径为r,根据平行证明△OED∽△ACD,列比例式代入即可求解
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径是( )
A.1 B.1.5 C.2 D.2.5
拓展提升
解:∵⊙O是Rt△ABC的内切囫,
∴OE 丄 BC,OF 丄 AC,
∴∠OFC=∠OEC=90°
∵∠ACB=90°,
∴四边形CFOE是矩形,
∵OE=OF,
∴矩形CFOE是正方形,
∴OF=EC,
拓展提升
设⊙O的半径为 r,则 DE=CD-CE=2-r,OE=r,
∵OE//AC,
∴△OED∽△ACD,
∴r=1.5,
故选B
