2.2 等腰三角形同步练习题（含答案）

中小学教育资源及组卷应用平台
等腰三角形 知识点针对练习
学校:______姓名:______班级:______考号:______
一、等腰三角形的定义
1.如图，每个小方格的边长都为两点都在小方格的顶点上，点也是图中小方格的顶点，并且是等腰三角形，那么点的个数为( )

A. B. C. D.
2.如图所示，在中，，点在上，且，则图中的等腰三角形有( )

A.个 B.个 C.个 D.个
3.已知等腰三角形中，腰，底，则这个三角形的周长为( )
A. B. C. D.
4.已知一个等腰三角形的两边长是和，则它的周长为( )
A. B. C.或 D.
5.如图，在中，若则腰是 ,底角是 .

6.如图，已知， ， 则图中共有 个等腰三角形，共有 个等边三角形.

7.量一量下面三角形的各边长，其中是等腰三角形(不包括等边三角形)的是 ，是等边三角形的是 ．(填序号)

8.如图，在中，，，点从点出发以每秒速度向点运动，点从点同时出发以每秒速度向点运动，其中一个动点到达端点，另一个动点也随之停止，当是以为底的等腰三角形时，运动的时间是 秒．

9.用一根长为的细绳围成一个等腰三角形．
(1)若腰长为，求底边长．
(2)如果腰长是底边长的倍，求这个三角形各边的长．
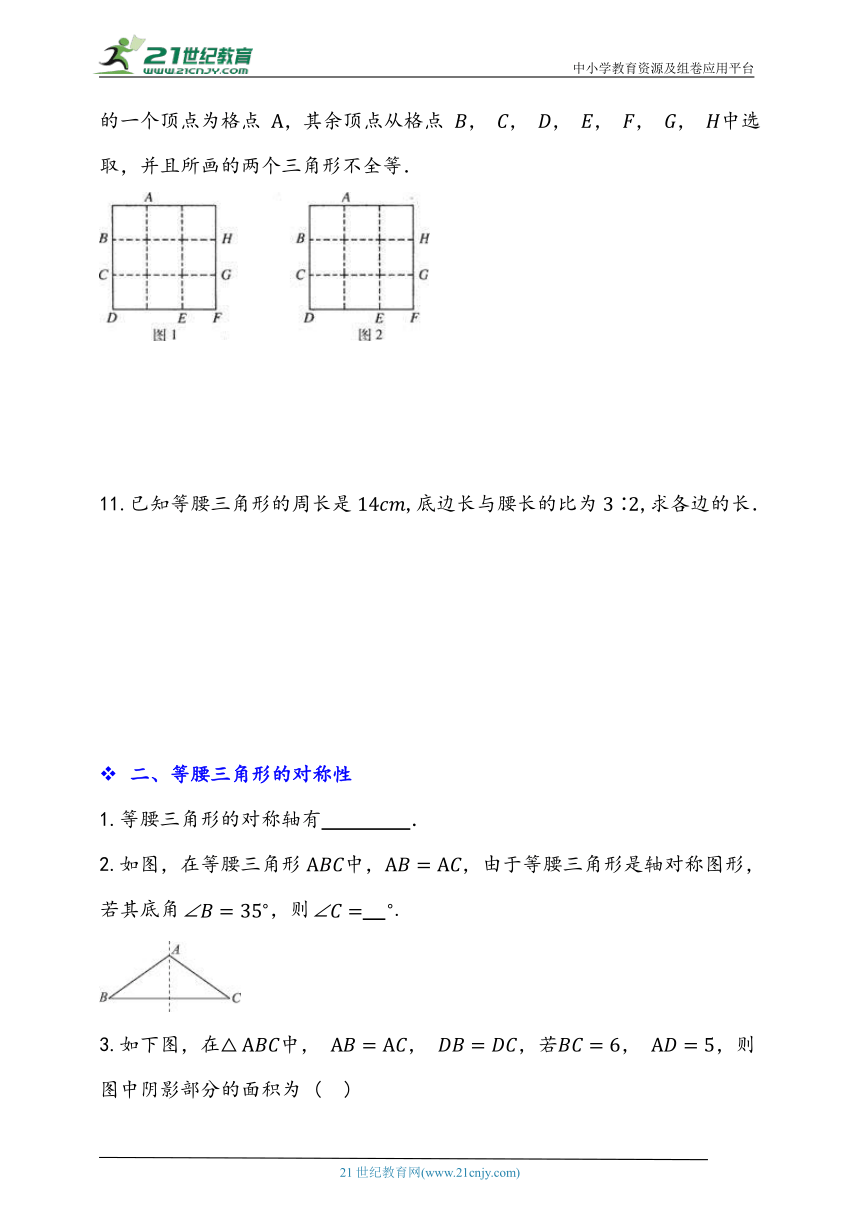
10.在正方形网格图、图中各画一个等腰三角形要求：每个等腰三角形的一个顶点为格点 ，其余顶点从格点 ， ， ， ， ， ， 中选取，并且所画的两个三角形不全等．

11.已知等腰三角形的周长是,底边长与腰长的比为∶,求各边的长．
二、等腰三角形的对称性
1.等腰三角形的对称轴有 ．
2.如图，在等腰三角形中，，由于等腰三角形是轴对称图形，若其底角，则 .

3.如下图，在中， ， ，若， ，则图中阴影部分的面积为 ( )

A. B. C. D.
4.如图，在中，，是边上的高，点、是的三等分点，若的面积为，则图中阴影部分的面积为( ).

A. B. C. D.
5.下列说法中，正确的是（ ）
A.直角三角形是轴对称图形 B.等腰三角形至少有一条对称轴
C.锐角三角形是轴对称图形 D.钝角三角形是轴对称图形
6.等腰三角形的对称轴是（ ）
A.顶角的平分线 B.底边上的高
C.底边上的中线 D.底边上的高所在的直线
7.如果三角形一边的中线和这边上的高重合，那么这个三角形是( )
A.等边三角形 B.等腰三角形 C.锐角三角形 D.钝角三角形
8.如图所示，用根火柴摆成个大小相同的等边三角形，请根据以下要求移动火柴：

(1)每次移走根火柴，使之减少个等边三角形，通过次移走，最终剩下个等边三角形(大小必须相同);
(2)每次移动根火柴，使之减少个等边三角形，通过次移动，最终剩下个等边三角形(大小可以相同)．
9.如图，在中，已知，于点，请仅用无刻度的直尺按要求画图．

(1)如图①，点为上任意一点，在上找一点，使；
(2)如图②，点为上任意一点，在上找一点，使．
10.如图，在中，，是的中点，点在上，利用轴对称的性质说明.

等腰三角形的定义参考答案
1.【答案】C
2.【答案】C
3.【答案】A
【解析】【分析】由于等腰三角形的两腰相等，题目给出了腰和底，根据周长的定义即可求解．
【解答】解：
．
故这个三角形的周长为．
故选：．
4.【答案】B
5.【答案】和；和
6.【答案】；
【解析】等腰三角形有等边三角形有.
7.【答案】③；⑤
8.【答案】
【解析】设运动的时间为，在中，，，
点从点出发以每秒的速度向点运动，点从点同时出发以每秒的速度向点运动，
当是等腰三角形时，，
，，
即，
解得．
故答案为：．
9.【答案】(1)，底边长为．
(2)设底边长为，则腰长为，，解得，，三角形三边长分别为．
10.【答案】解：下图供参考．



【解析】本题考查等腰三角形的画法，属开放题，难度较小．
【答案】设底边长为,
则一腰长为．
根据题意，得∶∶，
所以，解得.
.
所以此等腰三角形的腰长为,底边长为
【解析】设底边长为,
则一腰长为．
根据题意，得∶∶，
所以，解得.
.
所以此等腰三角形的腰长为,底边长为
等腰三角形的对称性参考答案
1.【答案】一条或三条
【解析】【分析】等腰三角形是轴对称图形，注意分一般等腰三角形和特殊等腰三角形两种情况考虑．
【解答】解：一般等腰三角形有一条，即底边上的中线所在的直线；若是特殊的等腰三角形即等边三角形，则有三条，即每条边上的中线所在的直线．
故答案为：一条或三条．
2.【答案】
3.【答案】C
4.【答案】C
【解析】由图，根据等腰三角形是轴对称图形知，和的面积相等，所以阴影部分的面积是三角形面积的一半．
∵，
∴阴影部分面积．
故选：．
5.【答案】B
6.【答案】D
7.【答案】B
【解析】线段垂直平分线上的点到线段两个端点的距离相等，所以是等腰三角形.
故选B.
8.【答案】(1)解：如图所示：

(2)如图所示：

9.【答案】(1)解：如图①，点即为所求；

(2)如图②，点即为所求．

10.【答案】∵，
∴是等腰三角形.
又∵是的中点，
∴直线是的对称轴，
∴、关于直线对称.
又∵点在上，
∴、关于直线对称.
∴由轴对称的性质得.
【解析】由，是的中点可知，直线是等腰的对称轴，、关于直线对称，点在上，所以、关于直线对称，则由轴对称的性质得.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)