全等三角形[下学期]

课件16张PPT。复习全等三角形比一比,谁的记忆好:
1、全等三角形的性质
2、全等三角形的定理对应边相等 ；对应角相等 ；周长相等 ；面积相等 SSS 三边对应相等的两个三角形全等
? ASA 角及它们的夹边对应相等的两个三角形全等
?? AAS 两角和其中一角的对边对应相等的两个三角形全等
SAS 两边及它们的夹角对应相等的两个三角形全等
HL（直角三角形全等判定） 一条直角边和斜边对应相 等的两个直角三角形全等 赛一赛，谁运用得最好：
1、全等三角形性质的运用
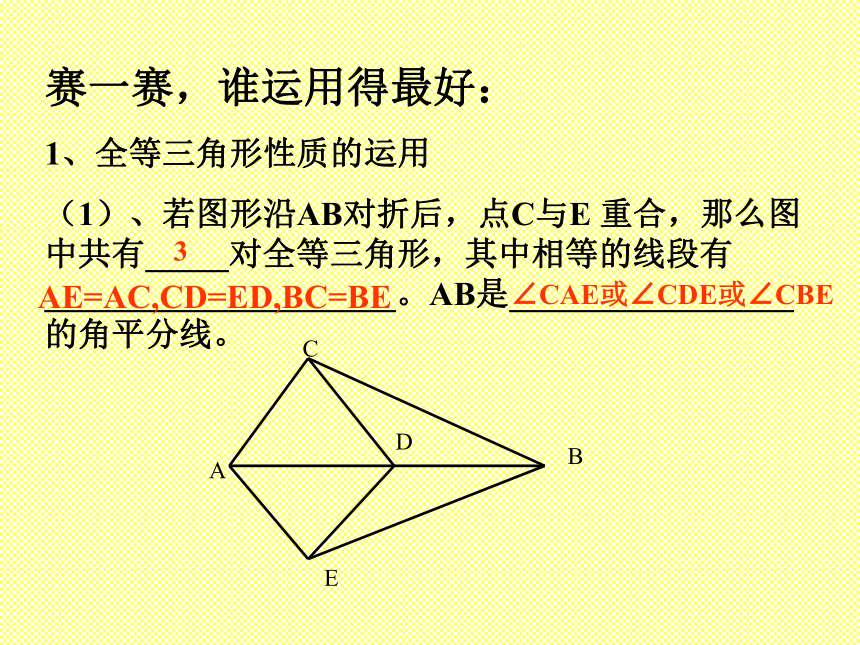
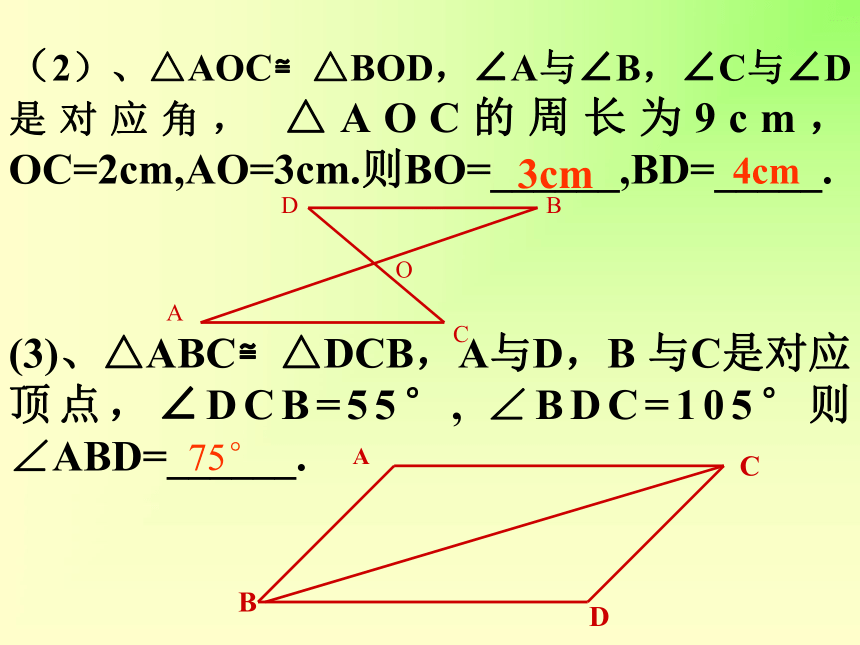
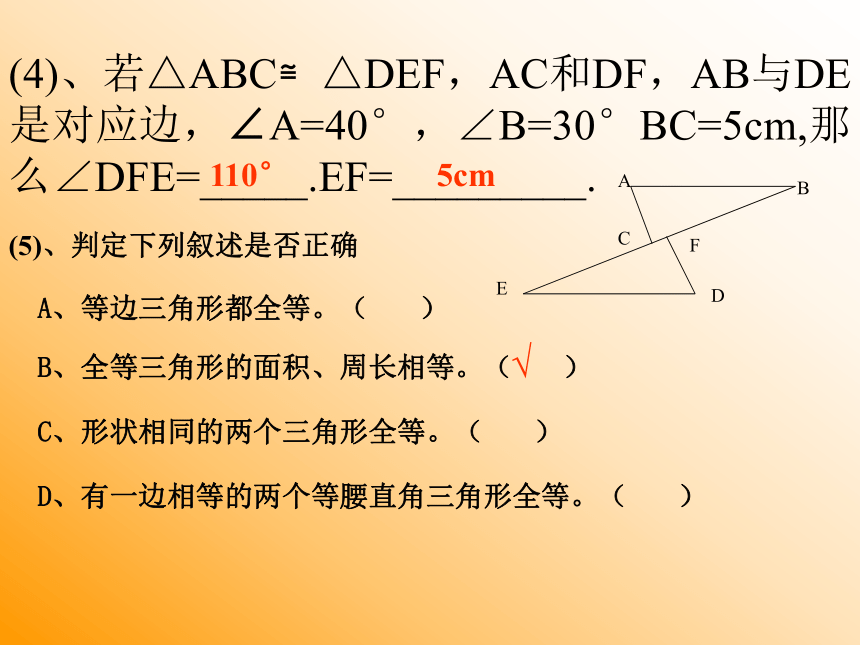
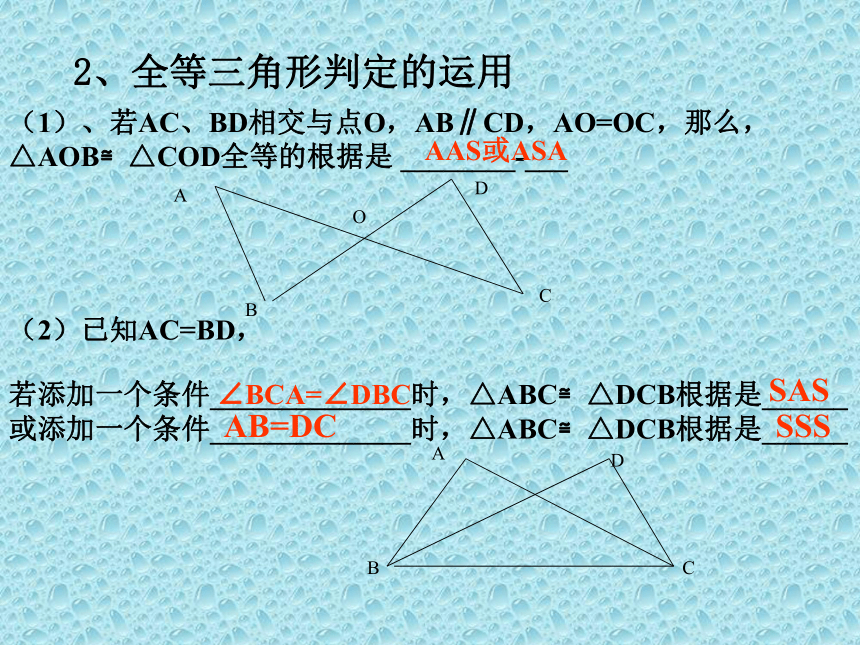
（1）、若图形沿AB对折后，点C与E 重合，那么图中共有_____对全等三角形，其中相等的线段有_____________________。AB是_________________的角平分线。 ACBED3AE=AC,CD=ED,BC=BE∠CAE或∠CDE或∠CBE（2）、△AOC≌△BOD，∠A与∠B，∠C与∠D是对应角， △AOC的周长为9cm， OC=2cm,AO=3cm.则BO=______,BD=_____. (3)、△ABC≌△DCB，A与D，B 与C是对应顶点，∠DCB=55°, ∠BDC=105°则∠ABD=______. ACDBOABCD3cm4cm75°(4)、若△ABC≌△DEF，AC和DF，AB与DE是对应边，∠A=40°，∠B=30°BC=5cm,那么∠DFE=_____.EF=_________. (5)、判定下列叙述是否正确 A、等边三角形都全等。（ ） B、全等三角形的面积、周长相等。（ ） C、形状相同的两个三角形全等。（ ） D、有一边相等的两个等腰直角三角形全等。（ ） 110°　5cm√ABCFED2、全等三角形判定的运用 （1）、若AC、BD相交与点O，AB∥CD，AO=OC，那么， △AOB≌△COD全等的根据是 ________-___
若添加一个条件______________时，△ABC≌△DCB根据是______
或添加一个条件______________时，△ABC≌△DCB根据是______
（2）已知AC=BD，AAS或ASA∠BCA=∠DBCSASAB=DCSSSBADCABDCO（3）、AD⊥BC，CE⊥AB，AD和CE交于H，若只添一个条件，
使△AEH≌△CEB，那么你会添什么呢？添条件_________,根据是___________.
( 4 )、在下列条件， 1、AB∥EF，AC∥DF ，BD=CE 2、AC=DF，BC=DE，AB=EF 3、∠A＝∠F，BC=DE，AB=EF 4、∠A ＝∠F，AB=EF，AC=FD 能判定△ABC≌△FED的是哪几个？ BE=HEASA1，2，4ABCEDHBAFEDC（5）、如果AB=AD，AC平分∠BAD，说出△ABC≌△ADC的理由： 解： ∵ AC平分∠BAD（ ） ∴ _____= ______(角平分线的意义) 在△ABC和△ADC中 AB=AD （ ）
______ = ______ AC=_____( ) ∴ △ABC≌△ADC( ) 已知∠BAC∠DAC已知∠BAC∠DACAC公共边SASABCD(6)、已知：如图，∠B=∠ C，AD=AE，说出AB=AC的理由： 解： 在△ABE和△ACD中， ∠B=______( ) ∠A=______( ) AE=_______( )
∴△ABE≌△ACD ( ) ∴AB=AC( ) ∠C已知∠A公共角AD已知AAS全等三角形对应边相等ACBED(7)、如图，CA=CB，CA⊥OA，CB⊥OB，则OC平分∠BOA，说明理由： 解： ∵CA⊥OA （ ） ∴∠CAO=90° （ ） ∵CB⊥OB （已知） ∴∠CBO=90° （ ）∴∠CAO=∠CBO在Rt△ACO和Rt△BCO中， AC=BC（ ） _______=________∴Rt△ACO≌Rt△BCO ( ) ∴___________= ___________( ) ∴OC平分∠BOA（角平分线的意义） 已知垂直的意义垂直的意义已知∠CAO∠CBOHL∠AOC∠BOC全等三角形对应角相等OADBFCE(8)、如图C是线段AB上一点，DC⊥CE， AE⊥AB，DB⊥AB，若CE=CD，试说明AC=BD的理由。解: ∵EA⊥AB，DB⊥AB
∴∠A=∠B（垂直的意义 ）
∵EC⊥CD
∴∠ECA+∠DCB=90°
∵∠E+∠ECA=90°
∴∠E=∠DCB（同角的余角相等）
在△ACE和△BDC中
∠A=∠B
∠E=∠DCB
EC=CD（ 已知 ）
∴△ACE≌△BDC（ AAS ）
∴BD=AC（全等三角形对应边相等） EACBD（9）已知：等腰三角形ABC中，F是BC中点，FE⊥AB， FD⊥AC ，试说明EF=DF的理由ABFCDE（10）、已知：∠A=∠D ，∠E=∠F，AB=CD，试说明△AGB≌△DHC 的理由解: ∵∠E+∠D+∠EBC=180°
∠A+∠F+∠FCA=180°（ 三角形内角和等于180° ）
又∵∠A=∠D，∠E=∠F
∴∠EBC=∠FCB
∵∠GBA+∠EBC=180°
∠HCD+∠FCB=180°
∴∠GBA=∠HCD（ 等角的补角相等）
在△AGB和△DHC中
∠A=∠D
AB=DC（已知 ）
∠GBA=∠HCD
∴△ABG≌△DHC（ ASA ）
ABCDEFGH3、知识的延伸： 已知：△ABC≌△A′B′C′，AD、A′D′分别是△ABC和△A′B′C′的中线，那么AD和A′D′相等吗？为什么？解： ∵△ABC≌△A′B′C′ （ ） ∴AB=_______,∠B=________.
BC=_________.( ) ∵AD、A′D′是BC、B′C′上的中线
∴BD=_________. 在△ABD和△A′B′D′中， AB=______ ∠B=________BD=______ ∴△ABD≌△A′B′D′ ( ) ∴AD=A′D′( ) 已知全等三角形对应边。对应角相等全等三角形对应边相等SASA′B′∠B′B′D′A′B′B′B′C′B′D′ABDCB`C`D`A`课内小结：