浙教版九年级数学上册1.4二次函数的应用 同步练习 (含答案)
文档属性
| 名称 | 浙教版九年级数学上册1.4二次函数的应用 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 546.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 10:13:19 | ||
图片预览



文档简介
浙教九上1.4二次函数的应用
(共18题)
一、选择题(共12题)
城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网 ”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用.名为“数据包络分析”(简称 )的一种效率评价方法,可以很好地优化出租车资源配置.为了解出租车资源的“供需匹配”,北京、上海等城市对每天 个时段的 值进行调查,调查发现, 值越大,说明匹配度越好.在某一段时间内,北京的 值 与时刻 的关系近似满足函数关系 (,, 是常数,且 ),如图记录了 个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻 是
A. B. C. D.
某旅行社要接团去外地旅游,经计算所获营业额 (元)与旅行团人数 (人)满足关系式 .若要使所获营业额最大,则此旅行团应有
A. 人 B. 人 C. 人 D. 人
如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度 (单位:)与水平距离 (单位:)近似满足函数关系 .下图记录了原子滑车在该路段运行的 与 的三组数据 ,,,根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离 满足
A. B. C. D.
心理学家发现:课堂上,学生对概念的接受能力 与提出概念的时间 (单位:)之间近似满足函数关系 , 值越大,表示接受能力越强.如图记录了学生学习某概念时 与 的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为
A. B. C. D.
某超市 月份的营业额为 万元,第一季度的营业额为 万元,如果平均每月增长率为 ,那么 与 的函数关系式是
A.
B.
C.
D.
已知抛物线 与 轴交于点 ,与直线 ( 为任意实数)相交于 , 两点,则下列结论不正确的是
A.存在实数 ,使得 为等腰三角形
B.存在实数 ,使得 的内角中有两角分别为 和
C.任意实数 ,使得 都为直角三角形
D.存在实数 ,使得 为等边三角形
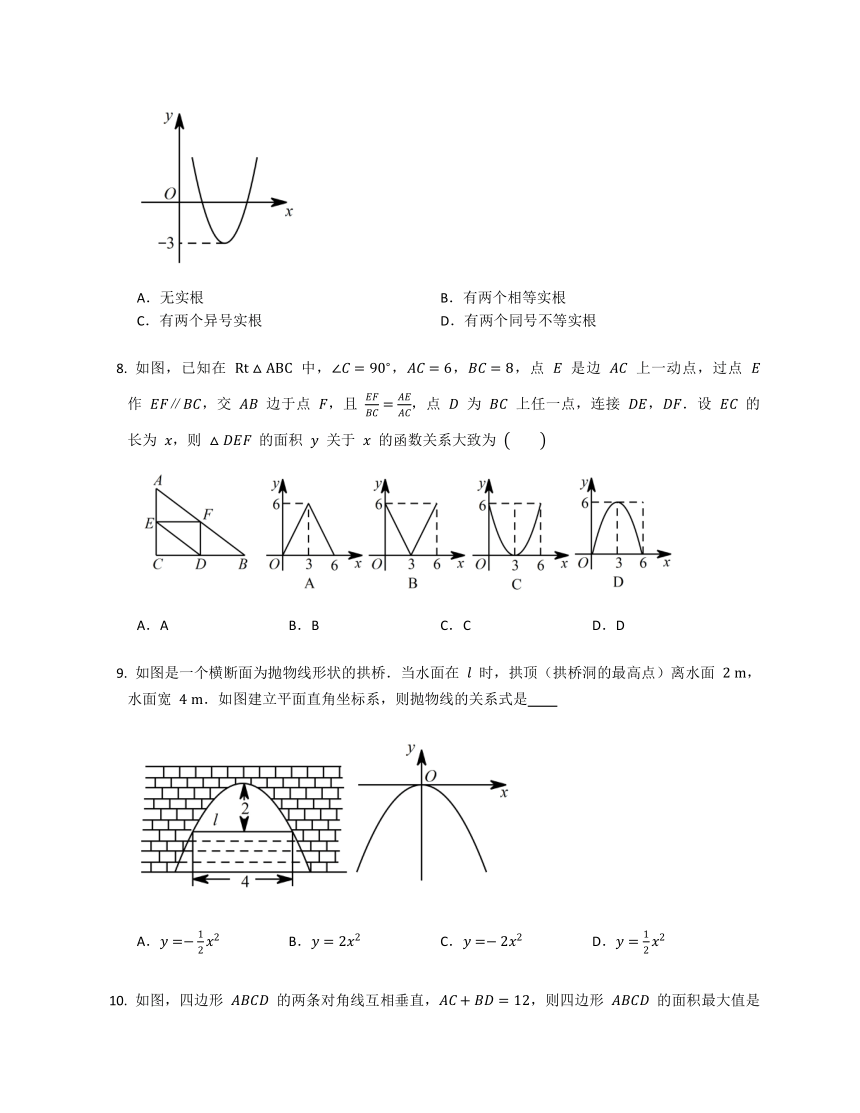
已知二次函数 的图象如图所示,那么关于 的方程 的根的情况是
A.无实根 B.有两个相等实根
C.有两个异号实根 D.有两个同号不等实根
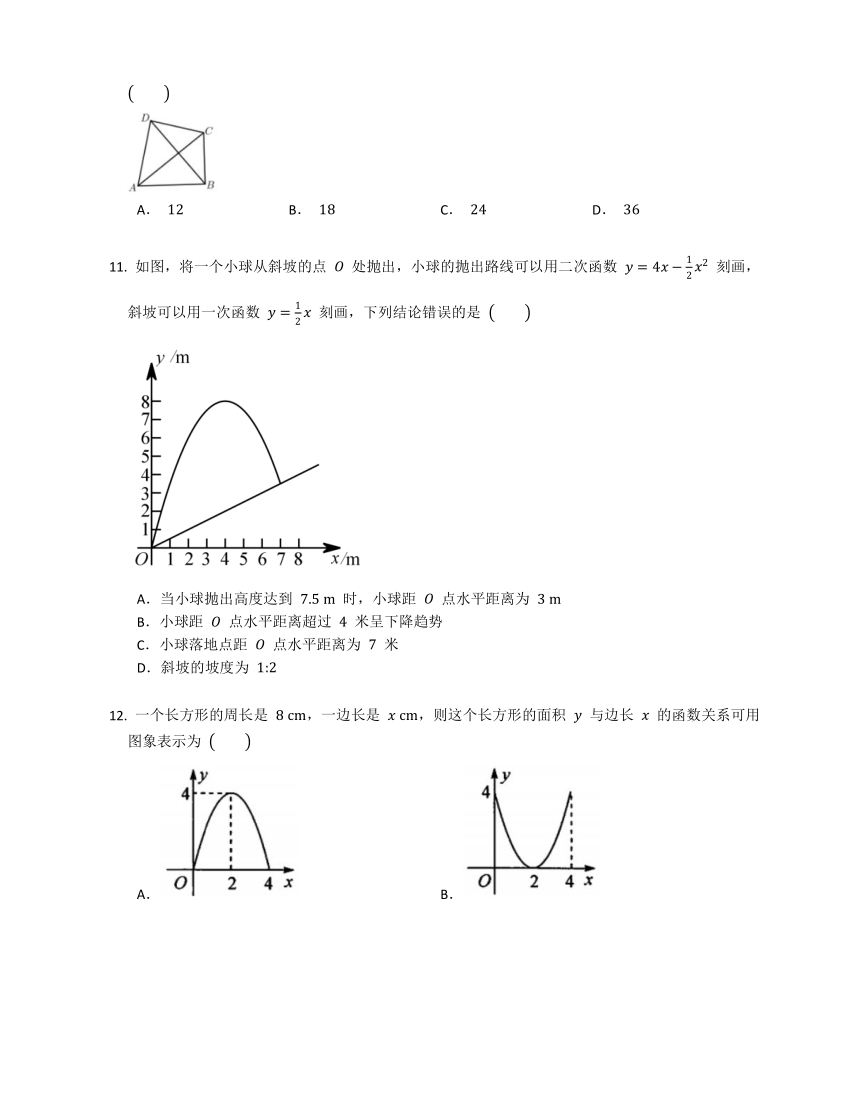
如图,已知在 中,,,,点 是边 上一动点,过点 作 ,交 边于点 ,且 ,点 为 上任一点,连接 ,.设 的长为 ,则 的面积 关于 的函数关系大致为
A.A B.B C.C D.D
如图是一个横断面为抛物线形状的拱桥.当水面在 时,拱顶(拱桥洞的最高点)离水面 ,水面宽 .如图建立平面直角坐标系,则抛物线的关系式是
A. B. C. D.
如图,四边形 的两条对角线互相垂直,,则四边形 的面积最大值是
A. B. C. D.
如图,将一个小球从斜坡的点 处抛出,小球的抛出路线可以用二次函数 刻画,斜坡可以用一次函数 刻画,下列结论错误的是
A.当小球抛出高度达到 时,小球距 点水平距离为
B.小球距 点水平距离超过 米呈下降趋势
C.小球落地点距 点水平距离为 米
D.斜坡的坡度为
一个长方形的周长是 ,一边长是 ,则这个长方形的面积 与边长 的函数关系可用图象表示为
A. B.
C. D.
二、填空题(共3题)
把 分成两个正数的和,设其中一个正数为 ,则所得两个正数的积 (用含 的代数式表示). 的最大值是 .
某商场四月份的营业额是 万元,如果该商场第二季度每个月营业额的增长率相同,都为 ,六月份的营业额为 万元,那么 关于 的函数解析式是 .
二次函数 的图象如图所示,根据图象解答下列问题:
()方程 的根是 .
()不等式 的解是 .
三、解答题(共3题)
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来积累利润 (万元)与销售时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).
根据图象提供的信息,解答下列问题:
(1) 由已知图象上的三点坐标,求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求第 个月公司所获利润是多少万元.
如图,以 的速度将小球沿与地面成 角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度 (单位:)与飞行时间 (单位:)之间具有函数关系 .
(1) 小球飞行时间是多少时,小球最高?最大高度是多少?
(2) 小球飞行时间 在什么范围时,飞行高度不低于 ?
把一个足球垂直水平地面向上踢,时间为 (秒)时该足球距离地面的高度 (米)适用公式 .
(1) 当 时,求足球距离地面的高度.
(2) 当足球距离地面的高度为 米时,求 .
(3) 若存在实数 ,,当 时,足球距离地面的高度都为 (米),求 的取值范围.
答案
一、选择题(共12题)
1. 【答案】C
2. 【答案】C
3. 【答案】B
【解析】由图可知 ,,,
将三组数据代入函数, 解得
,
当 时, 最小,
,,,
.
4. 【答案】B
5. 【答案】D
【解析】第一季度的营业额为一、二、三月份营业额之和,增长率为 ,则一月份营业额为 万.第二月增长了 万元.二月份的营业额为 万元,同理可推.
6. 【答案】D
【解析】如图 ,可以得 为等腰三角形,选项A正确;
如图 ,,,可以得 的内角中有两角分别为 和 ,选项B正确;
如图 和 ,,可以得 为直角三角形,选项C正确;
不存在实数 ,使得 为等边角形,选项D正确.
故选D.
7. 【答案】D
【解析】提示:令 ,则函数 是由函数 向上平移2个单位得到,故可画出图象如图:
根据图象可知:方程 有两个同号不等实根.
8. 【答案】D
9. 【答案】A
【解析】设抛物线的解析式为 .
由题意可知抛物线经过 .
.
抛物线的解析式为 .
10. 【答案】B
【解析】设 ,则 ,
,
,
,
当 时, 有最大值为 .
11. 【答案】A
12. 【答案】A
二、填空题(共3题)
13. 【答案】 ;
14. 【答案】
【解析】根据题意,得
15. 【答案】 , ;
三、解答题(共3题)
16. 【答案】
(1) 由图象可知其顶点坐标为 ,
故可设其函数关系式为:.
所求函数关系式的图象过 ,
于是得:,解得 .
所求函数关系式为:,即 .
答:累积利润 与时间 之间的函数关系式为:.
(2) 把 代入关系式,得 ;
把 代入关系式,得 ,.
答:第 个月公司所获利是 万元.
17. 【答案】
(1) 由已知可得,,
当 时, 有最大值 ,
小球飞行时间是 时,小球最高为 .
(2) 由题意:,解得 ,,
由图象可知,当 时,.
当 时,满足题意.
18. 【答案】
(1) 当 时,(米),
当 时,足球距离地面的高度为 米.
(2) ,
,
即 ,
解得: 或 ,
故经过 或 秒时,足球距离地面的高度为 米.
(3) ,
由题意得 , 是方程 的两个不相等的实数根,
,
,
故 的取值范围是 .
(共18题)
一、选择题(共12题)
城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网 ”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用.名为“数据包络分析”(简称 )的一种效率评价方法,可以很好地优化出租车资源配置.为了解出租车资源的“供需匹配”,北京、上海等城市对每天 个时段的 值进行调查,调查发现, 值越大,说明匹配度越好.在某一段时间内,北京的 值 与时刻 的关系近似满足函数关系 (,, 是常数,且 ),如图记录了 个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻 是
A. B. C. D.
某旅行社要接团去外地旅游,经计算所获营业额 (元)与旅行团人数 (人)满足关系式 .若要使所获营业额最大,则此旅行团应有
A. 人 B. 人 C. 人 D. 人
如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度 (单位:)与水平距离 (单位:)近似满足函数关系 .下图记录了原子滑车在该路段运行的 与 的三组数据 ,,,根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离 满足
A. B. C. D.
心理学家发现:课堂上,学生对概念的接受能力 与提出概念的时间 (单位:)之间近似满足函数关系 , 值越大,表示接受能力越强.如图记录了学生学习某概念时 与 的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为
A. B. C. D.
某超市 月份的营业额为 万元,第一季度的营业额为 万元,如果平均每月增长率为 ,那么 与 的函数关系式是
A.
B.
C.
D.
已知抛物线 与 轴交于点 ,与直线 ( 为任意实数)相交于 , 两点,则下列结论不正确的是
A.存在实数 ,使得 为等腰三角形
B.存在实数 ,使得 的内角中有两角分别为 和
C.任意实数 ,使得 都为直角三角形
D.存在实数 ,使得 为等边三角形
已知二次函数 的图象如图所示,那么关于 的方程 的根的情况是
A.无实根 B.有两个相等实根
C.有两个异号实根 D.有两个同号不等实根
如图,已知在 中,,,,点 是边 上一动点,过点 作 ,交 边于点 ,且 ,点 为 上任一点,连接 ,.设 的长为 ,则 的面积 关于 的函数关系大致为
A.A B.B C.C D.D
如图是一个横断面为抛物线形状的拱桥.当水面在 时,拱顶(拱桥洞的最高点)离水面 ,水面宽 .如图建立平面直角坐标系,则抛物线的关系式是
A. B. C. D.
如图,四边形 的两条对角线互相垂直,,则四边形 的面积最大值是
A. B. C. D.
如图,将一个小球从斜坡的点 处抛出,小球的抛出路线可以用二次函数 刻画,斜坡可以用一次函数 刻画,下列结论错误的是
A.当小球抛出高度达到 时,小球距 点水平距离为
B.小球距 点水平距离超过 米呈下降趋势
C.小球落地点距 点水平距离为 米
D.斜坡的坡度为
一个长方形的周长是 ,一边长是 ,则这个长方形的面积 与边长 的函数关系可用图象表示为
A. B.
C. D.
二、填空题(共3题)
把 分成两个正数的和,设其中一个正数为 ,则所得两个正数的积 (用含 的代数式表示). 的最大值是 .
某商场四月份的营业额是 万元,如果该商场第二季度每个月营业额的增长率相同,都为 ,六月份的营业额为 万元,那么 关于 的函数解析式是 .
二次函数 的图象如图所示,根据图象解答下列问题:
()方程 的根是 .
()不等式 的解是 .
三、解答题(共3题)
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来积累利润 (万元)与销售时间 (月)之间的关系(即前 个月的利润总和 与 之间的关系).
根据图象提供的信息,解答下列问题:
(1) 由已知图象上的三点坐标,求累积利润 (万元)与时间 (月)之间的函数关系式.
(2) 求第 个月公司所获利润是多少万元.
如图,以 的速度将小球沿与地面成 角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度 (单位:)与飞行时间 (单位:)之间具有函数关系 .
(1) 小球飞行时间是多少时,小球最高?最大高度是多少?
(2) 小球飞行时间 在什么范围时,飞行高度不低于 ?
把一个足球垂直水平地面向上踢,时间为 (秒)时该足球距离地面的高度 (米)适用公式 .
(1) 当 时,求足球距离地面的高度.
(2) 当足球距离地面的高度为 米时,求 .
(3) 若存在实数 ,,当 时,足球距离地面的高度都为 (米),求 的取值范围.
答案
一、选择题(共12题)
1. 【答案】C
2. 【答案】C
3. 【答案】B
【解析】由图可知 ,,,
将三组数据代入函数, 解得
,
当 时, 最小,
,,,
.
4. 【答案】B
5. 【答案】D
【解析】第一季度的营业额为一、二、三月份营业额之和,增长率为 ,则一月份营业额为 万.第二月增长了 万元.二月份的营业额为 万元,同理可推.
6. 【答案】D
【解析】如图 ,可以得 为等腰三角形,选项A正确;
如图 ,,,可以得 的内角中有两角分别为 和 ,选项B正确;
如图 和 ,,可以得 为直角三角形,选项C正确;
不存在实数 ,使得 为等边角形,选项D正确.
故选D.
7. 【答案】D
【解析】提示:令 ,则函数 是由函数 向上平移2个单位得到,故可画出图象如图:
根据图象可知:方程 有两个同号不等实根.
8. 【答案】D
9. 【答案】A
【解析】设抛物线的解析式为 .
由题意可知抛物线经过 .
.
抛物线的解析式为 .
10. 【答案】B
【解析】设 ,则 ,
,
,
,
当 时, 有最大值为 .
11. 【答案】A
12. 【答案】A
二、填空题(共3题)
13. 【答案】 ;
14. 【答案】
【解析】根据题意,得
15. 【答案】 , ;
三、解答题(共3题)
16. 【答案】
(1) 由图象可知其顶点坐标为 ,
故可设其函数关系式为:.
所求函数关系式的图象过 ,
于是得:,解得 .
所求函数关系式为:,即 .
答:累积利润 与时间 之间的函数关系式为:.
(2) 把 代入关系式,得 ;
把 代入关系式,得 ,.
答:第 个月公司所获利是 万元.
17. 【答案】
(1) 由已知可得,,
当 时, 有最大值 ,
小球飞行时间是 时,小球最高为 .
(2) 由题意:,解得 ,,
由图象可知,当 时,.
当 时,满足题意.
18. 【答案】
(1) 当 时,(米),
当 时,足球距离地面的高度为 米.
(2) ,
,
即 ,
解得: 或 ,
故经过 或 秒时,足球距离地面的高度为 米.
(3) ,
由题意得 , 是方程 的两个不相等的实数根,
,
,
故 的取值范围是 .
同课章节目录
