【独家】育英学校浙教版初中数学九年级上册 4.5相似三角形的性质及其应用(3) 课件
文档属性
| 名称 | 【独家】育英学校浙教版初中数学九年级上册 4.5相似三角形的性质及其应用(3) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-30 00:00:00 | ||
图片预览



文档简介
课件16张PPT。浙教版九(上)§第四章王金红 4.5相似三角形的性质及应用(3)回顾相似三角形的性质:
1 相似三角形的对应角相等,对应边成比例
2 相似三角形的周长之比等于相似比
3 相似三角形的面积之比等于相似比的平方
相似三角形对应边上的高之比,对应边上中线之比,对应角平分线之比等于相似比
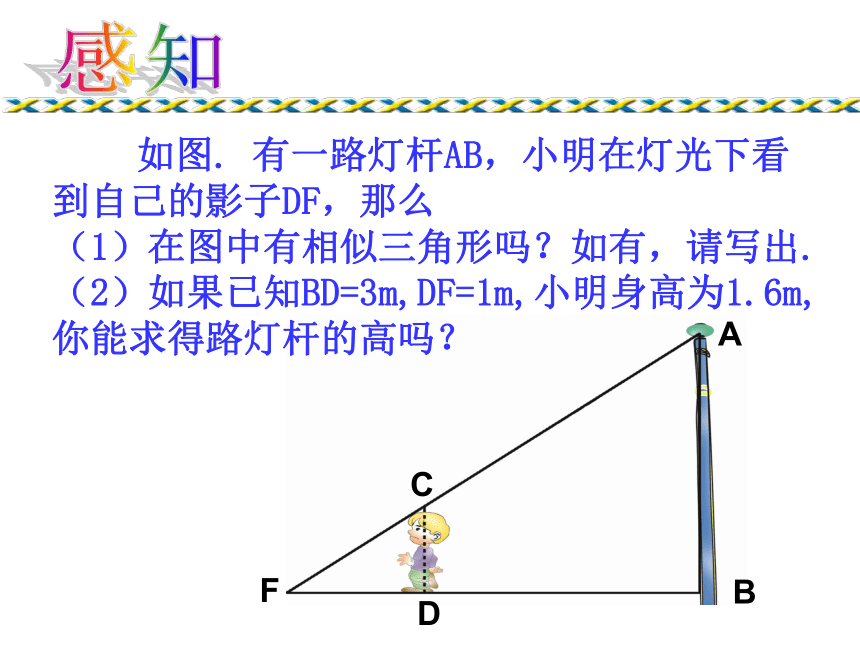
如图. 有一路灯杆AB,小明在灯光下看到自己的影子DF,那么
(1)在图中有相似三角形吗?如有,请写出.
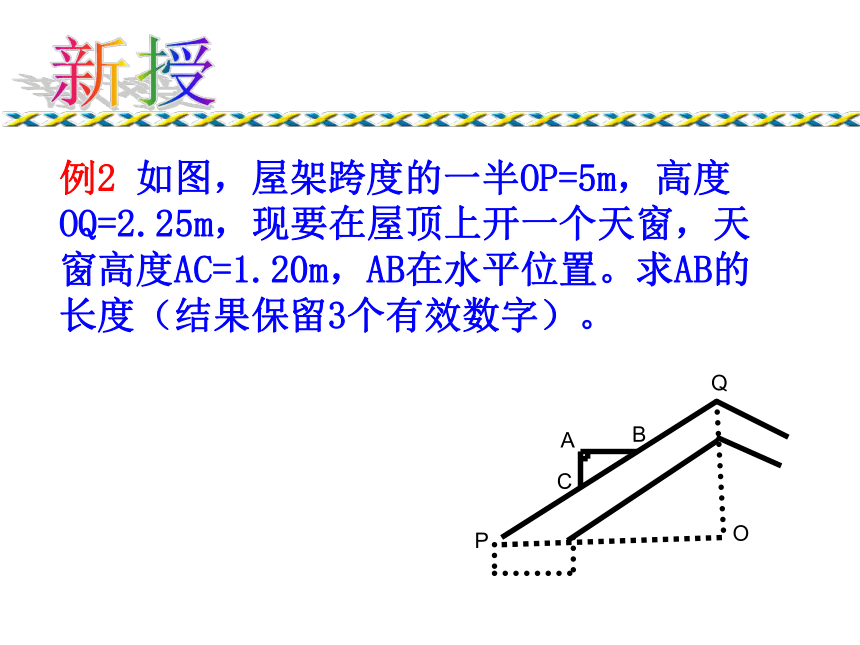
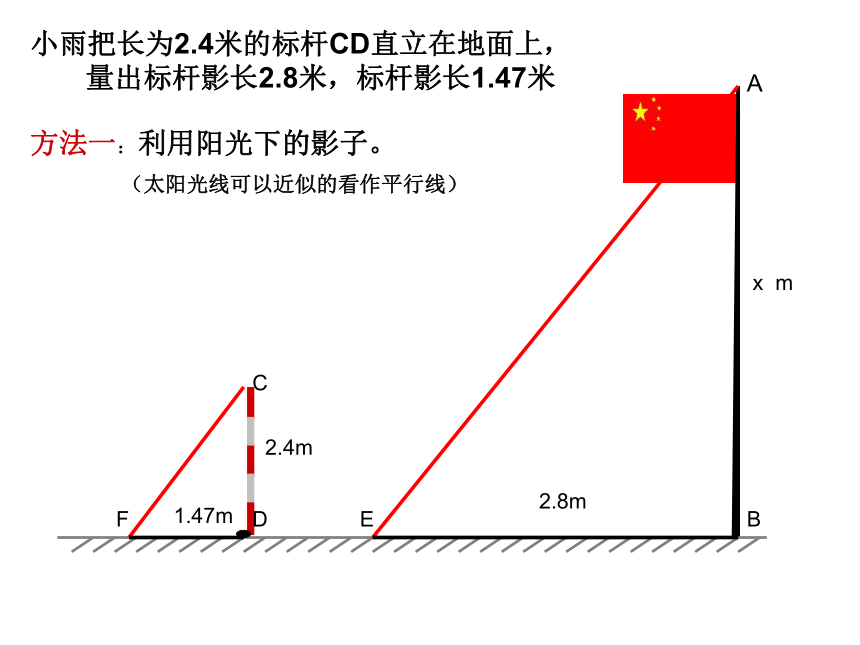
(2)如果已知BD=3m,DF=1m,小明身高为1.6m,你能求得路灯杆的高吗?ABDFC感知例2 如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置。求AB的长度(结果保留3个有效数字)。新授CPBOQA方法一:利用阳光下的影子。ABCDEF小雨把长为2.4米的标杆CD直立在地面上,
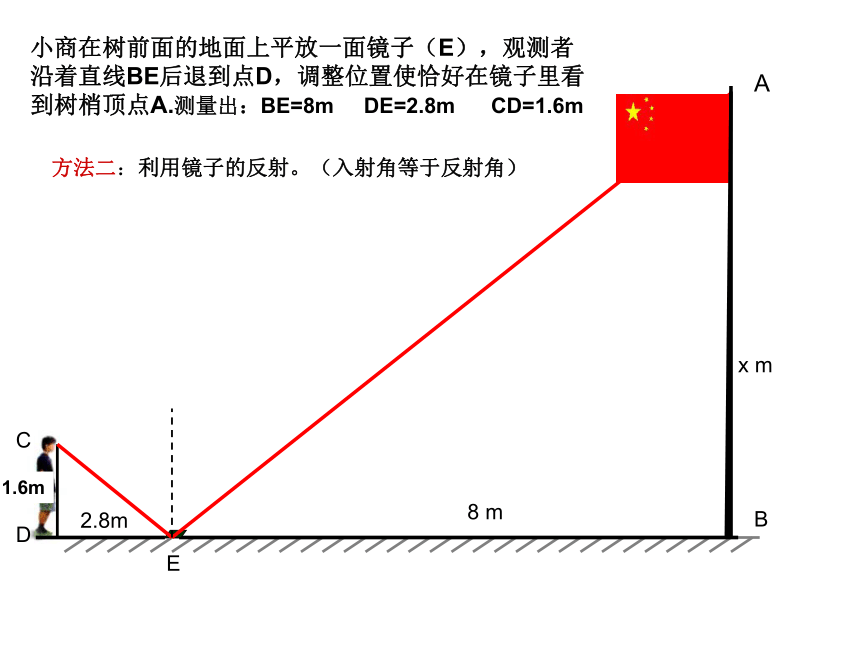
量出标杆影长2.8米,标杆影长1.47米(太阳光线可以近似的看作平行线)小商在树前面的地面上平放一面镜子(E),观测者沿着直线BE后退到点D,调整位置使恰好在镜子里看到树梢顶点A.测量出:BE=8m DE=2.8m CD=1.6m
ABECD方法二:利用镜子的反射。(入射角等于反射角)
ABCDEFGH 方法三:利用标杆
小明在地面直上立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E 、树梢的顶点A在同一直线上。测量:人与标杆的距离DF=1m,
人与树的距离DB=8
人的目高和标杆的高度EG=0.9m
人的高度CD=1.7mABCDEFGH方法四:利用标尺
用手举一根标尺EF,让标尺与地面垂直,调整人与树的距离或眼睛与标尺的距离,使标尺刚好挡住树的高度。测量:人与标尺的距离0.4m,
人与树的距离12m
确认标尺的长度0.3m依据:相似三角形对应高的比等于相似比。 步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。解:由题意得,△OAB∽ △OCD,解得:OF=20000(cm)
=200(m).基础演练小聪想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直
放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近
一楼房,影子不全落在地面上,有一部分落在墙上,他测得落
在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度. 变式一变式二小晨想测量旗杆的高度,他在某一时刻测得1米长的竹竿影长
0. 4米,在同时刻测量旗杆的影长时,影子不全落在地面上,
有一部分落在第一级台阶上,测得此影长为0.2米,一级台阶
高0.3米,此时落在地面上影长为4.4米,求旗杆的高度. 如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。分析:
如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。思考1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 2.铁道的栏杆的短臂为OA=1米,长臂OB=10米,短臂端下降AC=0.6米,则长臂端上升BD= 米。4米6体验3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)二、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 三、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题谈谈你的收获课堂小结
1 相似三角形的对应角相等,对应边成比例
2 相似三角形的周长之比等于相似比
3 相似三角形的面积之比等于相似比的平方
相似三角形对应边上的高之比,对应边上中线之比,对应角平分线之比等于相似比
如图. 有一路灯杆AB,小明在灯光下看到自己的影子DF,那么
(1)在图中有相似三角形吗?如有,请写出.
(2)如果已知BD=3m,DF=1m,小明身高为1.6m,你能求得路灯杆的高吗?ABDFC感知例2 如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置。求AB的长度(结果保留3个有效数字)。新授CPBOQA方法一:利用阳光下的影子。ABCDEF小雨把长为2.4米的标杆CD直立在地面上,
量出标杆影长2.8米,标杆影长1.47米(太阳光线可以近似的看作平行线)小商在树前面的地面上平放一面镜子(E),观测者沿着直线BE后退到点D,调整位置使恰好在镜子里看到树梢顶点A.测量出:BE=8m DE=2.8m CD=1.6m
ABECD方法二:利用镜子的反射。(入射角等于反射角)
ABCDEFGH 方法三:利用标杆
小明在地面直上立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E 、树梢的顶点A在同一直线上。测量:人与标杆的距离DF=1m,
人与树的距离DB=8
人的目高和标杆的高度EG=0.9m
人的高度CD=1.7mABCDEFGH方法四:利用标尺
用手举一根标尺EF,让标尺与地面垂直,调整人与树的距离或眼睛与标尺的距离,使标尺刚好挡住树的高度。测量:人与标尺的距离0.4m,
人与树的距离12m
确认标尺的长度0.3m依据:相似三角形对应高的比等于相似比。 步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2mm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。解:由题意得,△OAB∽ △OCD,解得:OF=20000(cm)
=200(m).基础演练小聪想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直
放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近
一楼房,影子不全落在地面上,有一部分落在墙上,他测得落
在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度. 变式一变式二小晨想测量旗杆的高度,他在某一时刻测得1米长的竹竿影长
0. 4米,在同时刻测量旗杆的影长时,影子不全落在地面上,
有一部分落在第一级台阶上,测得此影长为0.2米,一级台阶
高0.3米,此时落在地面上影长为4.4米,求旗杆的高度. 如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。分析:
如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。思考1.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为 . 2.铁道的栏杆的短臂为OA=1米,长臂OB=10米,短臂端下降AC=0.6米,则长臂端上升BD= 米。4米6体验3.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网5米的位置上,则拍击球的高度应为( ) 。A、2.7米 B、1.8米 C、0.9米 D、 6米 A一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)二、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 三、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题谈谈你的收获课堂小结
同课章节目录
