实数[上学期]

课件17张PPT。同学们好实数———浙教版 七年级上册课前练习：
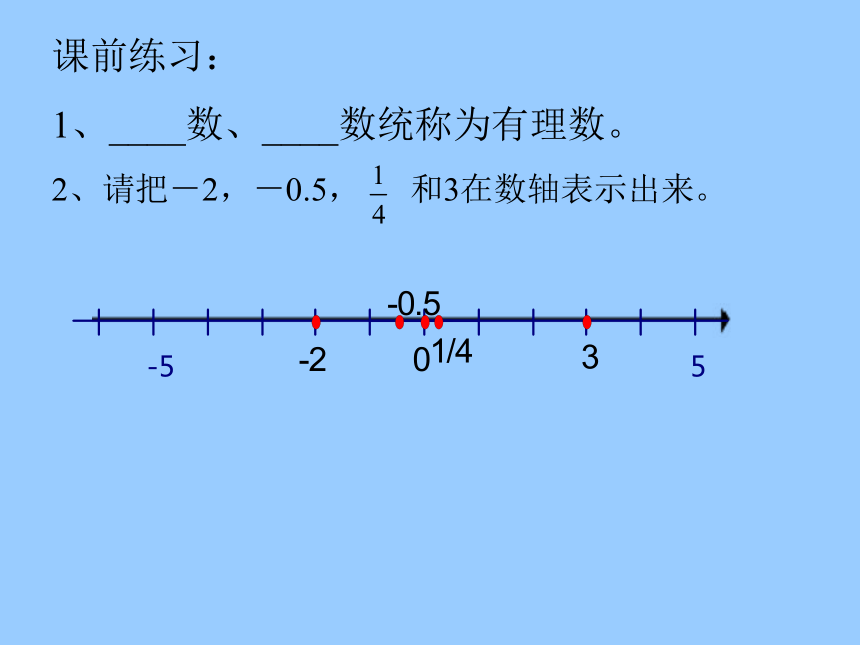
1、____数、____数统称为有理数。
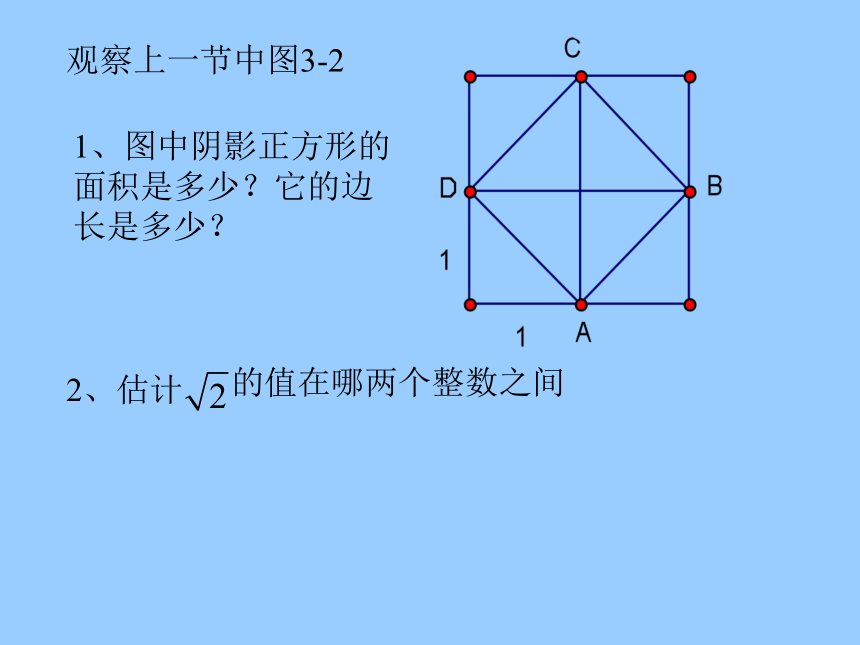
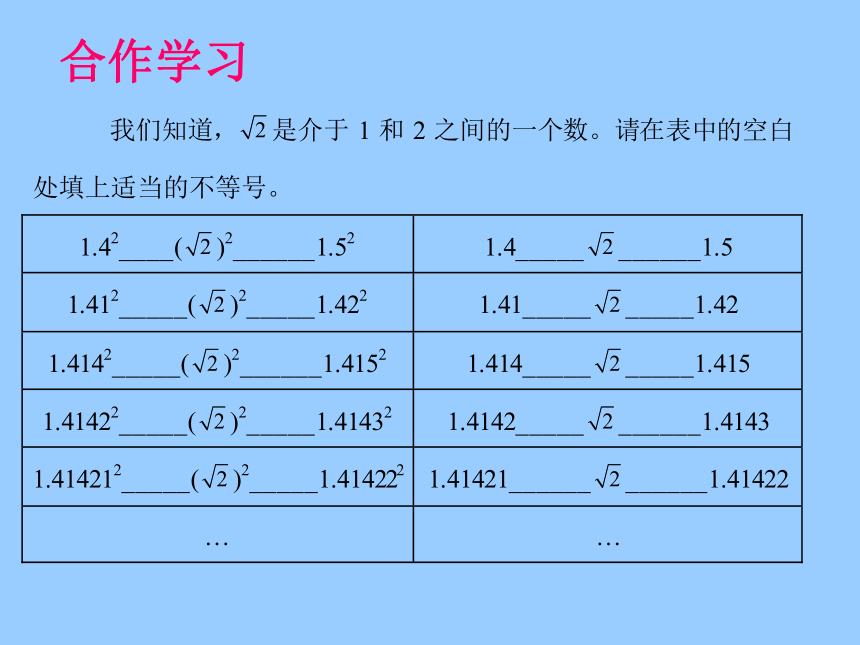
2、请把－2，－0.5，和3在数轴表示出来。观察上一节中图3-21、图中阴影正方形的面积是多少？它的边长是多少？2、估计的值在哪两个整数之间合作学习用上述方法可以得到一系列越来越接近的近似值。=1.414 213 562 373 095 048 801 688 724 209 6…那它是什么数呢？有理数整数
分数有限小数，无限循环小数像这种无限不循环小数叫做无理数讨论：如：Π=3.141 592 653 589 793 238 46…
√3=1.732 050 808…1.010010001…，-π，-√2，-√3都是无理数练习1：1、用“＜”“＞”号，或数字填空：(1)∵1.732____(√3)2_____1.742
∴1.73_____√3_______1.74
∴√3≈_________(结果保留2个有效数字)
(2)∵2.4492_______(√6)2______2.4502
∴2.449_______√6________2.450
∴√6≈_______(结果保留3个有效数字).
有理数和无理数统称实数。有理数有限小数，无限循环小数无理数正有理数负有理数零正无理数负无理数无限不循环小数实数练习2：在中，属于无理数的有：____________________________;
属于有理数的有:____________________________;
属于实数的有:_______________________________. 2600多年前，古希腊的毕达哥拉斯学派，非常崇拜数。认为“万物的本质都是数”，他们企图用数来解释一切。毕达哥拉斯学派有个叫希伯斯的年轻人，他对正方形的对角线问题很感兴趣。他根据勾股定理发现，正方形的对角线长和边长之比不能用整数比来表示。
这一发现，动摇了毕达哥拉斯学派的哲学基础，使他们大为惊恐，他们严密封锁希伯斯的发现，并规定谁要是泄露出去，就要处以极刑。
后来希伯斯还是把自己的发现传了出去，但他又十分害怕，就逃往家乡，想不到在他渡地中海时，被毕达哥拉斯学派的信徒追上，并把他投到海里，杀害了他。
无理数的发现。曾在西方引起了数学危机，然而在我国，对于古代希腊认为迷惑不解的开方不尽之数，早在公元1世纪的《九章算术》与随后的《九章算术列注》中就直截了当地“以面命之”，给出了独立成数的定义与某些运算法则，从而构成了整个实数系统。在《九章算术》里还介绍笔算开平方，国外直到公元5世纪才有开平方法的介绍。请看数轴:思考数轴上的点都表示有理数吗？你能把√2表示在数轴上吗?从数轴上来看,
在实数范围内,每一个数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数,我们说实数和数轴上的点一一对应.例 把下列实数表示在数轴上，并比较它们的大小（用“＜”连接）：
－1.4，√2，3.3，π，－√2，1.5解 －1.4，√2，3.3，π，－√2，1.5在数轴上表示如图
由图得 －√2＜－1.4＜√2＜1.5＜π＜3.3从以上数轴来看，
有理数扩充到实数后，有理数中的相反数和绝对值的概念依然适用。如，√2与－√2是互为相反数， √2 = －√2 =√2练习3：填空：
（1）－√3的相反数是_________;
(2) －√5 =_______;
(3)一个数的绝对值是π/2,则这个数是___________.从数轴上看:
在数轴上表示的两个实数,右边的数总比左边的数大.练习4
在 数轴上表示下列各数,并把它们按从小到大的顺序排列,用“＜”号连接:同学们再见