有理数总复习[上学期]

课件20张PPT。有 理 数 总 复 习一、有理数的基本概念二、有理数的运算1.负数 2.有理数 3.数轴
4.互为相反数
5.互为倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数与有效数字 加、减、乘、除、乘方运算一、有理数的基本概念1.负数：在正数前面加“—”的数；0既不是正数，也不是负数。判断：
1）a一定是正数；
2）－a一定是负数；
3）－（－a）一定大于0；
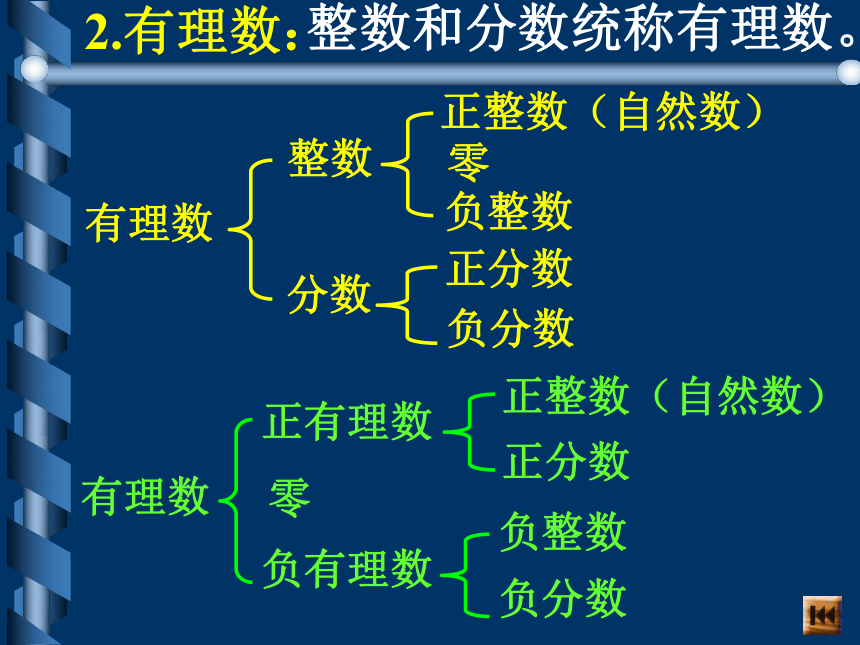
4）0是正整数。××××2.有理数：整数和分数统称有理数。有理数整数分数正整数（自然数） 零负整数正分数负分数有理数正有理数零负有理数正整数（自然数）正分数负整数负分数3.数 轴规定了原点、正方向和单位长度的直线.1）在数轴上表示的两个数，
右边的数总比左边的数大；2）正数都大于0,负数都小于0；
正数大于一切负数；3）所有有理数都可以用数轴上
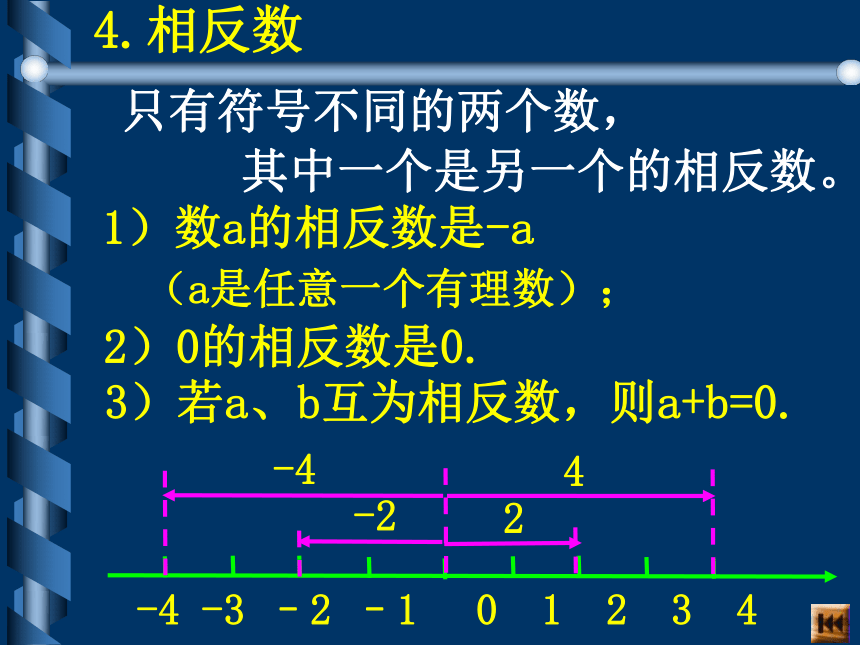
的点表示。4.相反数 只有符号不同的两个数，
其中一个是另一个的相反数。 1）数a的相反数是-a2）0的相反数是0. -22-443）若a、b互为相反数，则a+b=0. （a是任意一个有理数）；5.倒 数 乘积是1的两个数互为倒数 .1）a的倒数是 （a≠0）； 3）若a与b互为倒数，则ab=1.2）0没有倒数 ；例：下列各数，哪两个数互为倒数？
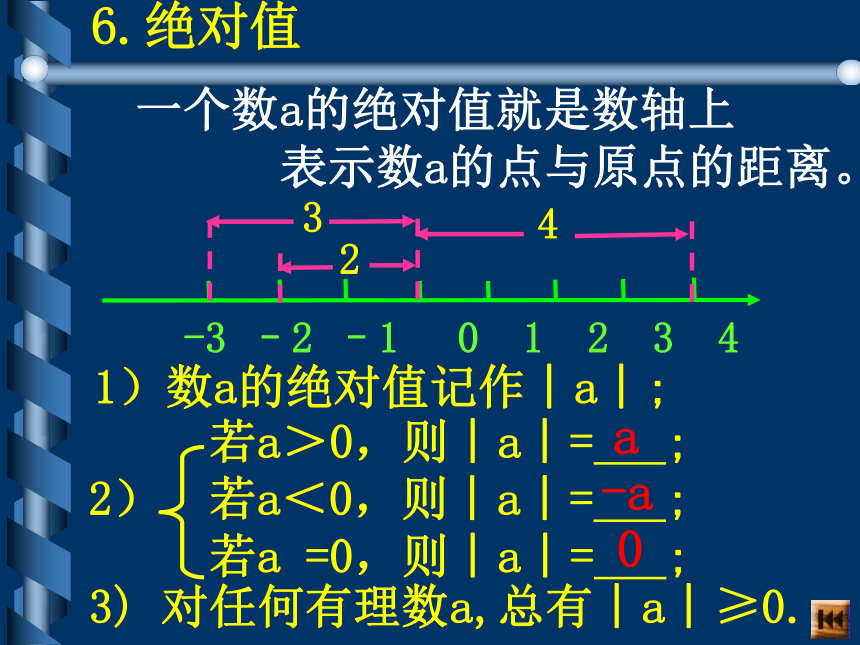
8， ，-1，+（-8），1，6.绝对值一个数a的绝对值就是数轴上
表示数a的点与原点的距离。1）数a的绝对值记作︱a︱; a-a03) 对任何有理数a,总有︱a︱≥0.7.有理数大小的比较1）可通过数轴比较：
在数轴上的两个数，右边的数
总比左边的数大；
正数都大于0，负数都小于0；
正数大于一切负数；
2）两个负数，绝对值大的反而小。
即:若a＜0,b＜0,且︱a︱＞︱b︱,
则a ＜ b.8.科学记数法、近似数与有效数字1. 把一个大于10的数记成a×10n
的形式，其中a是整数数位只有一位
的数，这种记数法叫做科学记数法 .2. 一个近似数，从左边第一个不是0
的数字起到，到精确到的数位止，所
有的数字，都叫做这个数的有效数字。 有理数的五种运算1.运算法则
2.运算顺序
3.运 算 律1.运算法则1）有理数加法法则
2）有理数减法法则
3）有理数乘法法则
4）有理数除法法则
5）有理数的乘方1)有理数加法法则① 同号两数相加,取相同的符号,并把绝对值相加；② 异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值
减去较小的绝对值；互为相反数
的两数相加得0； ③ 一个数同0相加,仍得这个数。若a>0,b<0,︱a︱>︱b︱, 则a+b=用数学语言描述有理数加法法则：①同号相加：
若a>0,b>0,则a+b=若a<0,b<0,则a+b=若a>0,b<0,︱a︱<︱b︱,
则a+b=②异号相加③与0相加若a、b互为相反数，则a+b=a是任一个有理数，则a+0=︱a︱+︱b︱-︱a︱-︱b︱(︱b︱-︱a︱)0a(︱a︱+︱b︱)-2)有理数减法法则 减去一个数，
等于加上这个数的相反数.
即 a-b=a+(-b)例：分别求出数轴上两点间的距离：
①表示2的点与表示-7的点；
②表示-3的点与表示-1的点。解：①︱2-（-7）︱=︱2+7︱=︱9︱=9
②︱-3-（-1）︱=︱-3+1︱=︱-2︱=23）有理数的乘法法则 两数相乘，同号得正，异号得负，并把绝对值相乘；
任何数同0相乘，都得0.① 几个不等于0的数相乘，积的符号
由负因数的个数决定，当负因数有奇
数个时，积为负；当负因数有偶数个
时，积为正.② 几个数相乘，有一个因数为0，
积就为0.用数学语言描述有理数乘法法则：①同号相乘
若a>0,b>0,则 ab=︱a︱×︱b︱若a<0,b<0,则 ab=︱a︱×︱b︱②异号相乘
若a>0,b<0,则 ab=若a<0,b>0,则 ab=︱a︱×︱b︱︱a︱×︱b︱③数与0相乘a为任何有理数，则 a×0=0++--4)有理数除法法则①除以一个数等于乘上这个数的倒数;

即a÷b=a× (b≠0)② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.5)有理数的乘方 ①求n个相同因数的积的运算,叫做乘方。②正数的任何次幂都是正数；
负数的奇次幂是负数，
负数的偶次幂是正数.2.运算顺序1）有括号，先算括号里面的；
2）先算乘方，再算乘除，
最后算加减；
3）对只含乘除，或只含加减的
运算，应从左往右运算。3.有理数的运算律1)加法交换律a+b=b+a2)加法结合律(a+b)+c=a+(b+c)3)乘法交换律ab=ba4)乘法结合律(ab)c=a(bc)5)分 配 律a(b+c)=ab+ac