3.5实数的复习

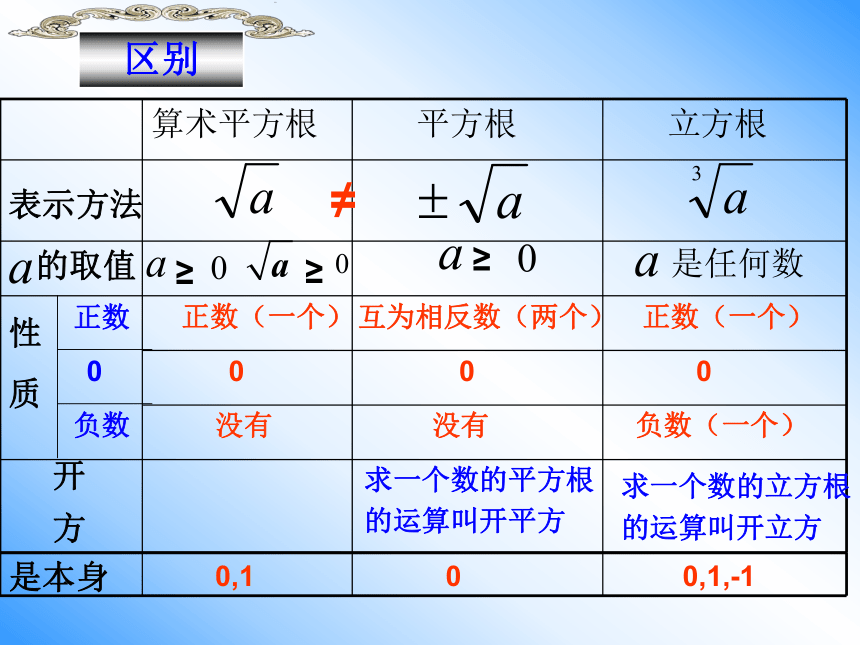
课件25张PPT。3.5 实数的复习１、平方根：
　①若　　　　，则　称为　的平方根，
　　即：
　　　　　　　　　　
　　　是被开方数，根指数是２，可以省略。
　② 正数有两个平方根，它们互为相反数，０的
　　平方根是０，负数没有平方根。
　③算术平方根：　　　　　　，它是一个非负数知识梳理2、立方根：
　①若　　　，则　称为是　的立方根，
　即：
　②一个正数有一个立方根，一个负数有一个立方
　根，０的立方根是０
　③恒等式：　　　
表示方法性
质开
方正数0负数正数（一个）0没有互为相反数（两个）0没有正数（一个）0负数（一个）求一个数的平方根
的运算叫开平方求一个数的立方根
的运算叫开立方≠是本身0,100,1,-1４、计算：
　　　　练一练１、判断：64的平方根是８
　　　　　８是64的平方根２、平方根是本身的数是（　　），算术平方根是本
　　身的数是（　　）。３、0.04的平方根是（　　），算术平方根是（　　），
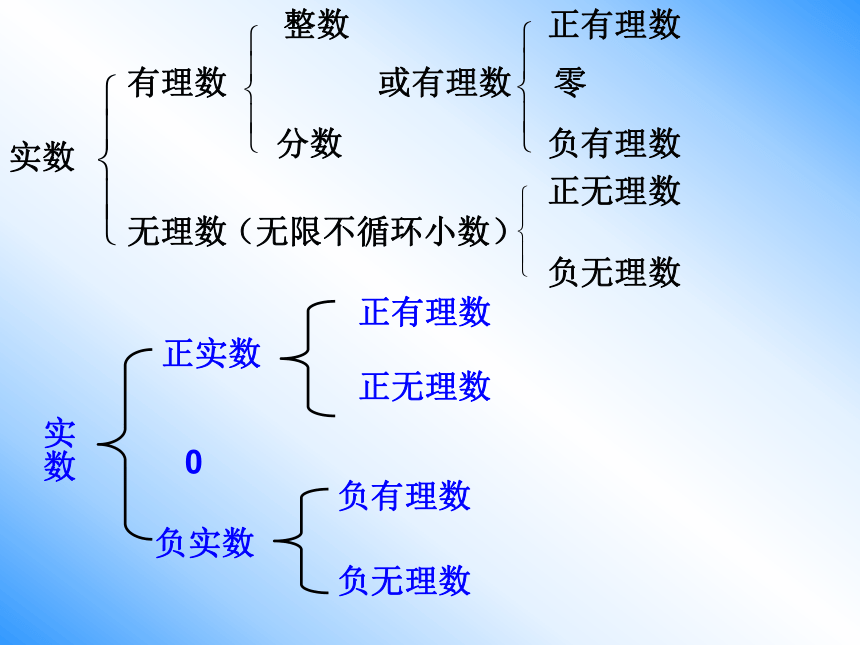
　　用符号表示为（　　）和（　　）。１、求下列各数的立方根：多学一点２、计算：３、若　　　　　　，则　的值是？3、实数：
①无理数：无限不循环小数
②无理数的常见形式：
开方开不尽的数；圆周率　，以及含有　的数；有规律但不循环的无限小数
③无理数的绝对值、相反数以及运算法则与有理数相似
④无理数在数轴上的近似表示和大小比较
⑤实数的分类：有理数和无理数统称为实数
⑥实数与数轴上的点一一对应解释: ①数轴上任何一点都可以用实数来表示②任何实数都可以表示在数轴上1.无理数有几个？
2.无理数都是用根号表示的数吗？
3.无理数都是开方开不尽的数吗？
4.用根号表示的数都是无理数吗？实数有理数正有理数负有理数零无理数正无理数负无理数或有理数整数分数（无限不循环小数）实数正实数 0负实数正有理数正无理数负有理数负无理数将下列各数分别填入下列的集合括号中自然数集合：分数集合：有理数集合：无理数集合：………在数轴上表示各数和它们的相反数，把这些数按从小到大的顺序排列，并用”<“号连接：求下列各数的相反数、倒数和绝对值：22－77下列说法正确的是：（1）无限小数是无理数（2）有理数都是有限小数（3）一个数的立方根不一定是无理数（4）任何实数都有唯一的立方根（5）只有正实数才有算术平方根√×××（6）任何数的平方根有两个，它们互为相反数×（7）不带根号的数都是有理数×√（8）两个无理数的和一定是无理数（9）两个无理数的积一定是无理数××（10）若正数a的一个平方根是b，那么a的另一个平方根是-b.若a为有理数,b为无理数,则ab必为无理数√√××（11）正数的两个平方根的和为0（12）没有平方根的数也没有立方根1.选择题：(1)、(-3)2的算术平方根是（ ）（A）无意义（B）±3（C）-3（D） 3(2)下列运算正确的是（ ）DA(3)下列各组数中，互为相反数的是（ ）（A）（B）（C）（D）B2．若 ，则 （　）．
(A) －0.7　 (B) ±0.7　 (C) 0.7　 (D) 0.49
3.下列说法中正确的是（　）．
(A)﹣3的平方根是 9 (B) 没有平方根
(C)
(D)如果 ,则 是正数或0。 4．若 ， ，则 （　）
(A) 716　 (B) 76.1　 (C) 7610　 (D) 0.761４、实数的运算：
实数的运算法则：先算乘方和开方，再算乘和除，最后算加和减，有括号的先算括号里的。巩固练习：
１、判断：不要搞错了64±884先填写下表,然后通过观察回答问题:(1)被开方数a（a≥0）的小数点位置移动的位数和它的算术平方根的小数点位置移动的位数之间有无规律？若有规律，请写出它们的移动规律. 0.0010.010. 1110100a=3240000 被开方数a（a≥0）的小数点向右（或向左）每移动两位，它的算术平方根的小数点就向右（或向左）移动一位.先填写下表,然后通过观察回答问题:(1)被开方数a的小数点向右（或向左）每移动三位时，你能探究出它的立方根的小数点移动规律吗？0.010.1110100…35.65-0.3565 被开方数a的小数点向右（或向左）每移动三位，它的立方根的小数点就向右（或向左）移动一位.掌握规律若　　　　　 　，则± 　　　　= 。 巩固练习 1、写出大于　　　且小于　　的所有整数。2、　　　的相反数是 ；绝对值是 。3、在数轴上表示　　的点与表示　　　的距离是？　　　　　　4、写出下列各数的整数部分和小数部分5、　　　界于哪两个整数之间？6、化简：　　　　　　　　　= .7.①求下列各数的平方根②求下列各数的立方根③求下列各式的值提高自我3.如图，数轴上表示1、　的对应点分别为A、B，点B关于点A的对称点为C，则点C所表示的数是（ ）已知按一定规律排列的一组数，1，，，……，，如果从中选出若干个数使它们的和大于3，
那么至少要选出几个数？