3.7正多边形
图片预览



文档简介
课件18张PPT。请你在纸上画一个正三角形和一个正方形你是怎么画的你?活动13.7 正多边形(1)问题1,什么样的图形是正多边形?各边相等,各角也相等的多边形是正多边形.活动1问题2,日常生活中,我们经常能看到正多边形的物体,利用正多边形,我们也可以得到许多美丽的图案,你还能举出一些这样的例子吗?例1 已知一个正多边形的内角为176.4°,这个正多边形是几边行?有没有内角为100°的正多边形?活动1
1.如果正多边形的一个外角等于45°,那么它的边数为 ( )
A.6 B.7
C.8 D.9【对点自测】A.正十二边形 B.正十边形
?C.正八边形 D.正六边形CB ( ) 3.正三角形外接圆的半径为R,则三角形边长为 ( )A4.正八边形如图3-7-1所示,点A,B,C是它的顶点,则∠ABC=___________.图3-7-122.5°你知道正多边形与圆的关系吗? 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.活动2 如图, 把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B = ∠C = ∠D = ∠E.又五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的 外接圆.我们以圆内接正五边形为例证明.∵弧AB=弧BC=弧CD=弧DE=弧EA,弧BCE=弧CDA,正多边形每一边所对的圆心角叫做正多边形的中心角.我们把一个正多边形外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).因此,亭子地基的周长l =4×6=24(m).利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr活动3练习1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不一定是正多边形.因为四条边不一定都相等;菱形不一定是正多边形.因为四个角不一定都相等;正方形是正多边形.因为四条边都相等,四个角都相等.活动42. 各边相等的圆内接多边形是正多边形吗?各角都相等的圆内接多边形呢?如果是,说明为什么;如果不是,举出反例.各边相等的圆内接多边形是正多边形.多边形A1A2A3A4…An是⊙O的内接多边形,且A1A2=A2A3=A3A4=…=An-1An,∴ 多边形A1A2A3A4…An是正多边形.∴弧A1A2=弧A2A3=弧A3A4=…=弧An-1An=弧AnA1,∴弧A2A3An=弧A3A4A1=
弧A4A5A2=…=弧A1A2An-1,
3.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的边BC上的高AD,垂足为D.连接OB,则OB=R.在Rt△OBD中 , ∠OBD=30°,边心距=OD=在Rt△ABD中 , ∠BAD=30°,·ABCDO由勾股定理,求得AB=解:连接OB,OC,过点O 作OE⊥BC垂足为E.
则∠OEB=90°,∠OBE= ∠ BOE=45°.Rt△OBE为等腰直角三角形.则有·ABCDOE例如,我们可以这样来画一个边长为2cm的正六边形.
第一种方法,如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O
1.如果正多边形的一个外角等于45°,那么它的边数为 ( )
A.6 B.7
C.8 D.9【对点自测】A.正十二边形 B.正十边形
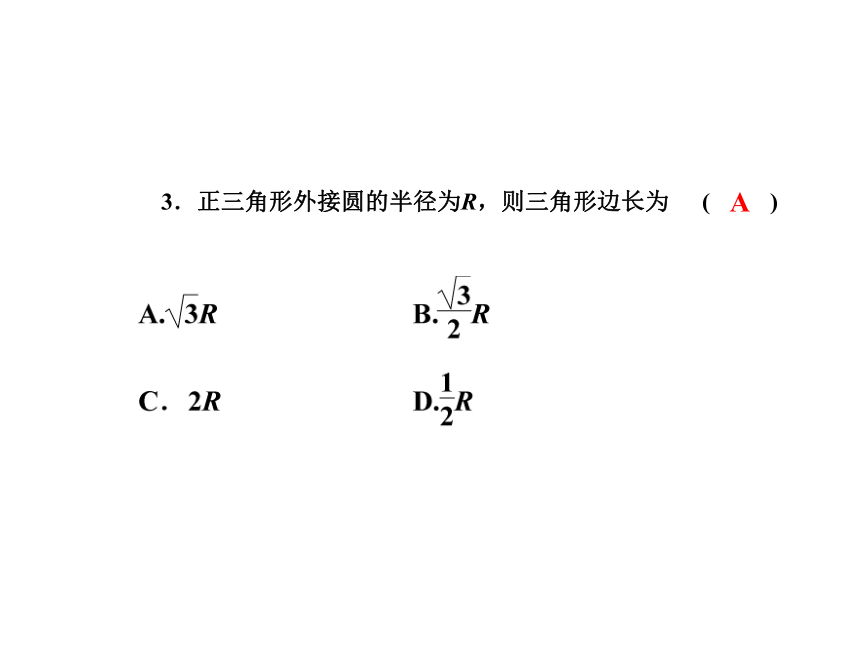
?C.正八边形 D.正六边形CB ( ) 3.正三角形外接圆的半径为R,则三角形边长为 ( )A4.正八边形如图3-7-1所示,点A,B,C是它的顶点,则∠ABC=___________.图3-7-122.5°你知道正多边形与圆的关系吗? 正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.活动2 如图, 把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴ AB=BC=CD=DE=EA,∴ ∠A=∠B.同理∠B = ∠C = ∠D = ∠E.又五边形ABCDE的顶点都在⊙O上,∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的 外接圆.我们以圆内接正五边形为例证明.∵弧AB=弧BC=弧CD=弧DE=弧EA,弧BCE=弧CDA,正多边形每一边所对的圆心角叫做正多边形的中心角.我们把一个正多边形外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).因此,亭子地基的周长l =4×6=24(m).利用勾股定理,可得边心距亭子地基的面积OABCDEFRPr活动3练习1. 矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不一定是正多边形.因为四条边不一定都相等;菱形不一定是正多边形.因为四个角不一定都相等;正方形是正多边形.因为四条边都相等,四个角都相等.活动42. 各边相等的圆内接多边形是正多边形吗?各角都相等的圆内接多边形呢?如果是,说明为什么;如果不是,举出反例.各边相等的圆内接多边形是正多边形.多边形A1A2A3A4…An是⊙O的内接多边形,且A1A2=A2A3=A3A4=…=An-1An,∴ 多边形A1A2A3A4…An是正多边形.∴弧A1A2=弧A2A3=弧A3A4=…=弧An-1An=弧AnA1,∴弧A2A3An=弧A3A4A1=
弧A4A5A2=…=弧A1A2An-1,
3.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.解:作等边△ABC的边BC上的高AD,垂足为D.连接OB,则OB=R.在Rt△OBD中 , ∠OBD=30°,边心距=OD=在Rt△ABD中 , ∠BAD=30°,·ABCDO由勾股定理,求得AB=解:连接OB,OC,过点O 作OE⊥BC垂足为E.
则∠OEB=90°,∠OBE= ∠ BOE=45°.Rt△OBE为等腰直角三角形.则有·ABCDOE例如,我们可以这样来画一个边长为2cm的正六边形.
第一种方法,如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这
条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.·O利用这种方法可以画出任意的正n边形.第二种方法,如图,以2cm为半径作一个⊙O,由于正六边形的半径等于边长,所以在圆上依次截取等于2cm的弦,就可以将圆六等分,顺次连接各分点即可.·O
同课章节目录
