2022-2023学年数学浙教版八年级下册4.2平行四边形及其性质 同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年数学浙教版八年级下册4.2平行四边形及其性质 同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 99.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 00:00:00 | ||
图片预览


文档简介
4.2平行四边形及其性质同步练习
选择题
1、如图,AB∥EF,C是EF上一个动点,当点C的位置变化时,△ABC的面积将( )
A.变大 B.变小
C.不变 D.变大变小要看点C向左还是向右移动
2、已知在四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC ②AD=BC ③OA=OC ④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.2种 B.3种 C.4种 D.5种
3、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4,则△CEF的面积是( )
A.4 B.3 C.2 D.
填空题
1、已知三角形ABC的面积为15cm2,AC=5cm,直线DE过点B且平行
于AC,则DE与AC之间的距离为____________ .
.木工师傅要检验一块长方形木板的一组对边是否平行,先用直角尺的一边紧靠木板边缘,读出与这边相对的另一边缘在直角尺上的刻度,换一个位置再读一次.试问这两次的读数相是否相等______
3、如图,在 ABCD中,∠A=70°,将 ABCD绕顶点B顺时针旋转到 A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=___________.
三、解答题
1.如图,在 ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.
(1)从对称性质看, ABCD是_________对称图形;
(2)求平行四边形ABCD的周长.
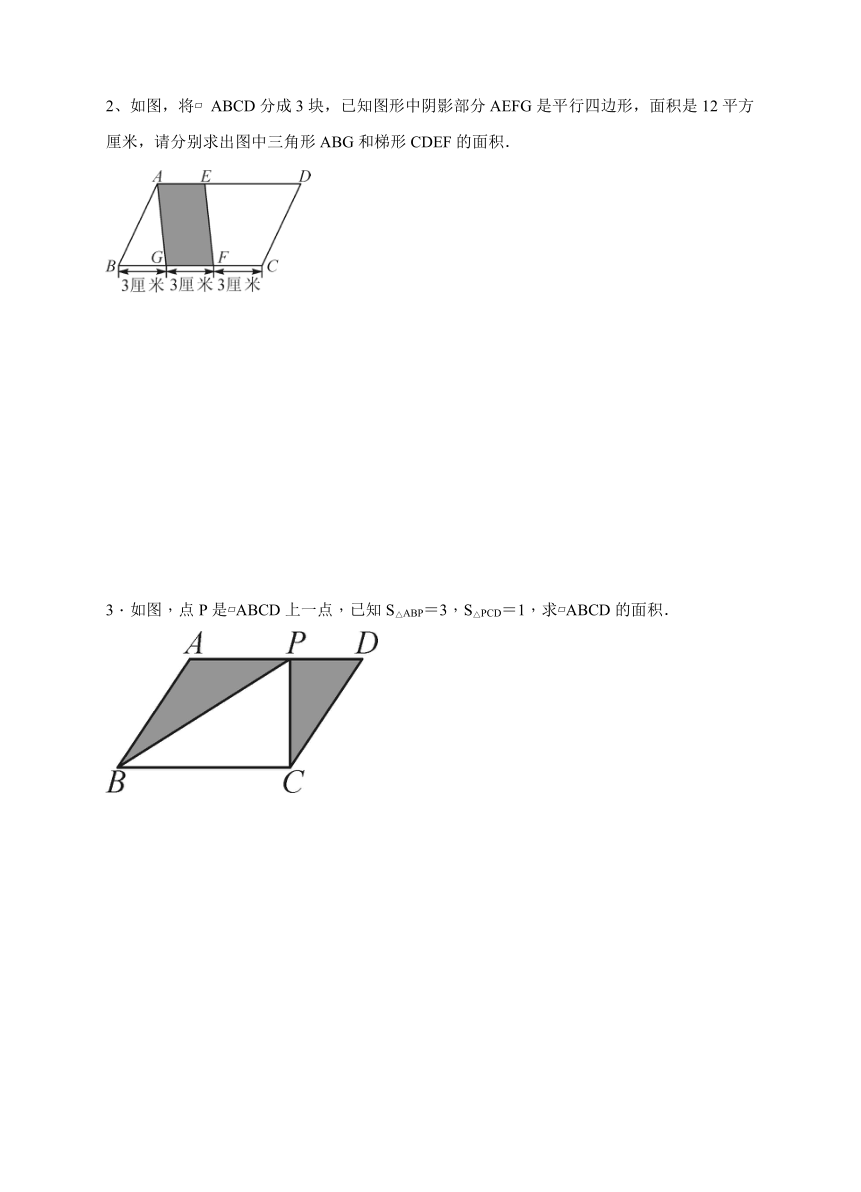
2、如图,将 ABCD分成3块,已知图形中阴影部分AEFG是平行四边形,面积是12平方厘米,请分别求出图中三角形ABG和梯形CDEF的面积.
3.如图,点P是 ABCD上一点,已知S△ABP=3,S△PCD=1,求 ABCD的面积.
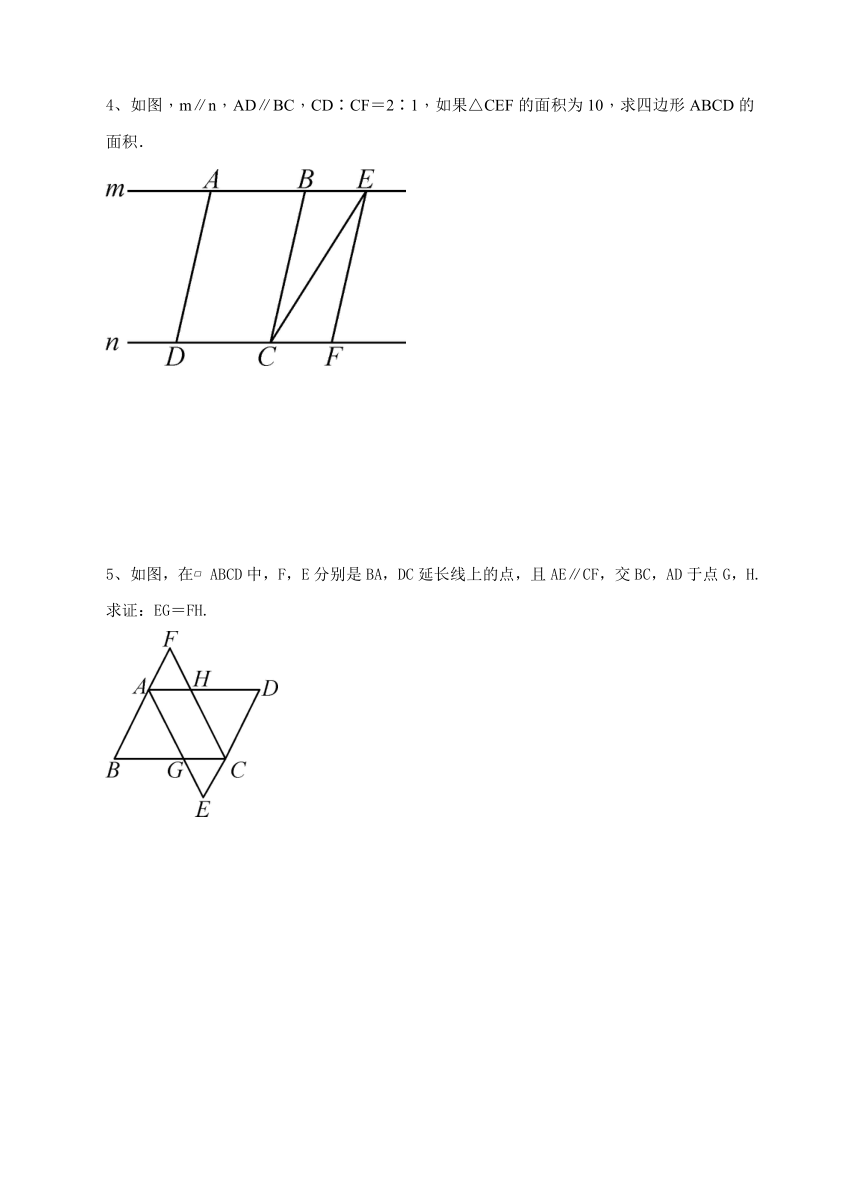
4、如图,m∥n,AD∥BC,CD∶CF=2∶1,如果△CEF的面积为10,求四边形ABCD的面积.
如图,在 ABCD中,F,E分别是BA,DC延长线上的点,且AE∥CF,交BC,AD于点G,H.求证:EG=FH.
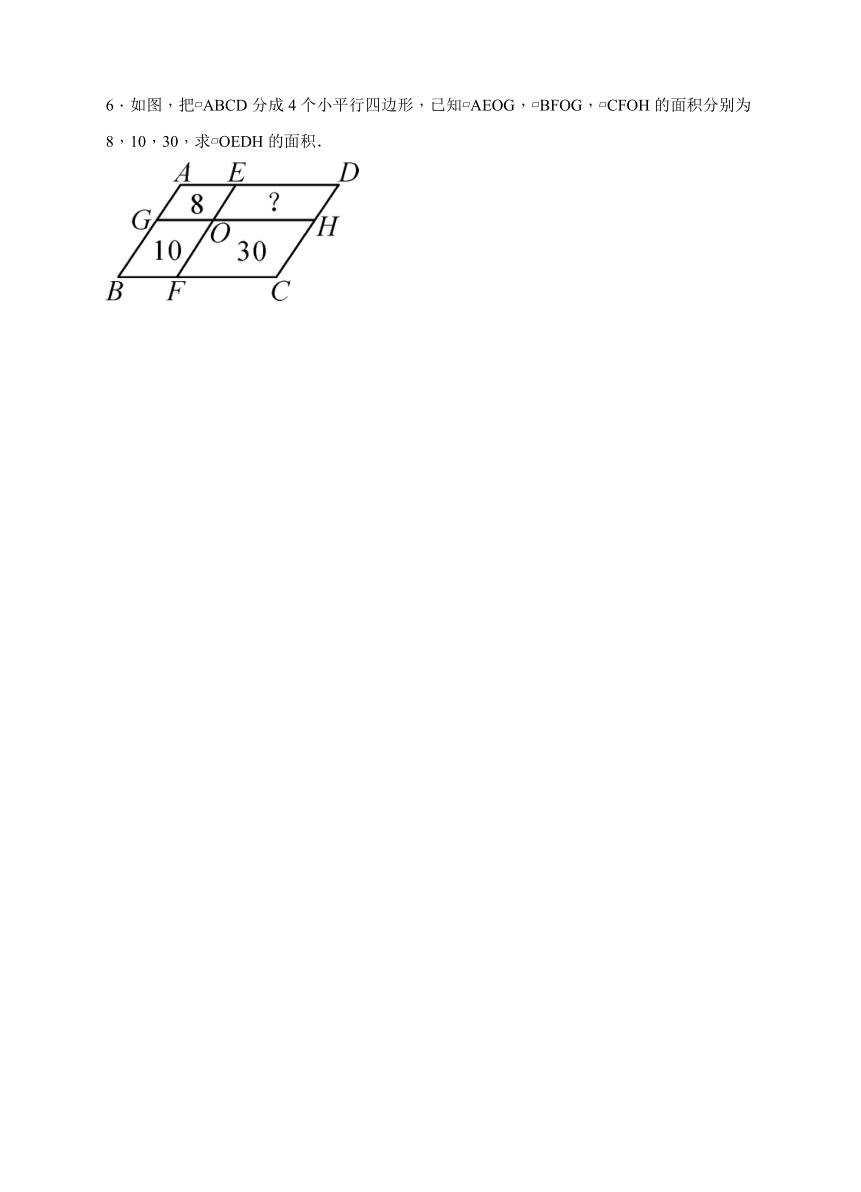
6.如图,把 ABCD分成4个小平行四边形,已知 AEOG, BFOG, CFOH的面积分别为8,10,30,求 OEDH的面积.
参考答案
一、选择题
C
【解析】 △ABC面积与AB及两平行线的距离不变.
C
【解析】
试题分析:(1)∵①AD∥BC ②AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(2)∵③OA=OC ④OB=OD
∴四边形ABCD为平行四边形(对角线互相平分的四边形是平行四边形)
(3)①AD∥BC ③OA=OC
∵①AD∥BC
∴∠OAD=∠OCB,∠ODA=∠OBC
∵③OA=OC
∴△OAD≌△OCB
∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(4)①AD∥BC ④OB=OD
∵①AD∥BC
∴∠OAD=∠OCB,∠ODA=∠OBC
∵④OB=OD
∴△OAD≌△OCB
∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
所以有4种选法,故选C
3、C
【解析】∵BG⊥AE
∴∠AGB=90°
∴AG=
∵AF平分∠BAD
∴∠BAE=∠FAD
∵四边形ABCD是平行四边形
∴AD//BC,BC=AD=9,AB//CD
∴∠DAF=∠AEB
∴∠BAE=∠AEB
∴BE=AB=6,AE=2AG=4
∴CE=BC-BE=3,S△ABE=AE·BG÷2=8
∵AB//CD
∴△ABE∽△FCE
∴
∴S△CEF=2
故选C
二、填空题
1、6cm
【解析】 DE与AC之间的距离就是三角形ABC底边AC边上高线的
长度,设此高长为xcm,则 ×5×x=15,解得x=6.
2、相等
【解析】 两次读数相等.长方形对边平行,又直角尺两次位置平行,由两平行线间的平行线段长度相等得读数相等.
3.40°
【解析】.
试题分析:∵ ABCD绕顶点B顺时针旋转到 A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=70°,
∴∠C=∠C1=70°,
∴∠BCC1=∠C1,
∴∠CBC1=180°﹣2×70°=40°,
∴∠ABA1=40°.
故答案是40°.
三、解答题
1、【解】 (1)中心;(2)40
【解析】
试题分析:(1)根据平行四边形的性质可知:对角线互相平分,所以O为旋转中心,即平行四边形ABCD是中心对称图形;(2)根据平行四边形中对角、对边分别相等,∠B=∠ADC=60°,再根据已知边长,由勾股定理可求出AB、AD的长,进而可求出平行四边形ABCD的周长.
试题解析:1)∵四边形ABCD是平行四边形,
∴对角线互相平分,
∴O为旋转中心,
即平行四边形ABCD是中心对称图形,
(2)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AB=CD,AD=BC.
∵AE⊥BC,
∵BE=4,
∴AB=8,
∴CD=AB=8,
∵CF=2,∴DF=6,
∵AF⊥DC,∠D=60°
∴在Rt△ADF中,AD=12,
∴平行四边形ABCD的周长=2(12+8)=40.
2、【解】 解:分别过点A作AM⊥BC于M,CN⊥AD于N,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=9 cm,
∴AM=CN,∵S AEFG=GF·AM,∴AM===4(cm),
∴CN=AM=4 cm,∵四边形AEFG是平行四边形,∴AE=GF=3 cm,
∴DE=6 cm,∴S△ABG=BG·AM=6(cm2),
S梯形CDEF=(CF+DE)·CN=18(cm2)
3、【解】 解:过点B作BM⊥AD,交DA的延长线于点M,过点C作CN⊥AD于点N,∵四边形ABCD是平行四边形,∴AD∥BC,∴AM=CN,∴S△ABP+S△PCD=AP·BM+DP·CN=AP·BM+DP·BM=BM(AP+DP)=AD·BM=S ABCD,∴S ABCD=2(S△ABP+S△PCD)=2(3+1)=8
4、【解】解:过点A作AG⊥n于点G,EH⊥n于点H,∵m∥n,
∴AG=EH,∵AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,又∵S△CEF=CF·EH=10,CD∶CF=2∶1,
∴S ABCD=CD·AG=2CF·EH=40
5、解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∵AB∥CD,AE∥CF,∴AE=CF,∵AD∥BC,
AE∥CF,∴AG=CH,∴AE-AG=CF-CH,即EG=FH
6、解:设平行线AD,GH之间的距离为h1,
平行线GH,BC之间的距离为h2,则==
,==,∴=,
即=,∴S OEDH=24
选择题
1、如图,AB∥EF,C是EF上一个动点,当点C的位置变化时,△ABC的面积将( )
A.变大 B.变小
C.不变 D.变大变小要看点C向左还是向右移动
2、已知在四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC ②AD=BC ③OA=OC ④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.2种 B.3种 C.4种 D.5种
3、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=4,则△CEF的面积是( )
A.4 B.3 C.2 D.
填空题
1、已知三角形ABC的面积为15cm2,AC=5cm,直线DE过点B且平行
于AC,则DE与AC之间的距离为____________ .
.木工师傅要检验一块长方形木板的一组对边是否平行,先用直角尺的一边紧靠木板边缘,读出与这边相对的另一边缘在直角尺上的刻度,换一个位置再读一次.试问这两次的读数相是否相等______
3、如图,在 ABCD中,∠A=70°,将 ABCD绕顶点B顺时针旋转到 A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=___________.
三、解答题
1.如图,在 ABCD中,AE⊥BC,AF⊥DC,垂足分别为E、F,∠ADC=60°,BE=4,CF=2.
(1)从对称性质看, ABCD是_________对称图形;
(2)求平行四边形ABCD的周长.
2、如图,将 ABCD分成3块,已知图形中阴影部分AEFG是平行四边形,面积是12平方厘米,请分别求出图中三角形ABG和梯形CDEF的面积.
3.如图,点P是 ABCD上一点,已知S△ABP=3,S△PCD=1,求 ABCD的面积.
4、如图,m∥n,AD∥BC,CD∶CF=2∶1,如果△CEF的面积为10,求四边形ABCD的面积.
如图,在 ABCD中,F,E分别是BA,DC延长线上的点,且AE∥CF,交BC,AD于点G,H.求证:EG=FH.
6.如图,把 ABCD分成4个小平行四边形,已知 AEOG, BFOG, CFOH的面积分别为8,10,30,求 OEDH的面积.
参考答案
一、选择题
C
【解析】 △ABC面积与AB及两平行线的距离不变.
C
【解析】
试题分析:(1)∵①AD∥BC ②AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(2)∵③OA=OC ④OB=OD
∴四边形ABCD为平行四边形(对角线互相平分的四边形是平行四边形)
(3)①AD∥BC ③OA=OC
∵①AD∥BC
∴∠OAD=∠OCB,∠ODA=∠OBC
∵③OA=OC
∴△OAD≌△OCB
∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
(4)①AD∥BC ④OB=OD
∵①AD∥BC
∴∠OAD=∠OCB,∠ODA=∠OBC
∵④OB=OD
∴△OAD≌△OCB
∴AD=BC
∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)
所以有4种选法,故选C
3、C
【解析】∵BG⊥AE
∴∠AGB=90°
∴AG=
∵AF平分∠BAD
∴∠BAE=∠FAD
∵四边形ABCD是平行四边形
∴AD//BC,BC=AD=9,AB//CD
∴∠DAF=∠AEB
∴∠BAE=∠AEB
∴BE=AB=6,AE=2AG=4
∴CE=BC-BE=3,S△ABE=AE·BG÷2=8
∵AB//CD
∴△ABE∽△FCE
∴
∴S△CEF=2
故选C
二、填空题
1、6cm
【解析】 DE与AC之间的距离就是三角形ABC底边AC边上高线的
长度,设此高长为xcm,则 ×5×x=15,解得x=6.
2、相等
【解析】 两次读数相等.长方形对边平行,又直角尺两次位置平行,由两平行线间的平行线段长度相等得读数相等.
3.40°
【解析】.
试题分析:∵ ABCD绕顶点B顺时针旋转到 A1BC1D1,
∴BC=BC1,
∴∠BCC1=∠C1,
∵∠A=70°,
∴∠C=∠C1=70°,
∴∠BCC1=∠C1,
∴∠CBC1=180°﹣2×70°=40°,
∴∠ABA1=40°.
故答案是40°.
三、解答题
1、【解】 (1)中心;(2)40
【解析】
试题分析:(1)根据平行四边形的性质可知:对角线互相平分,所以O为旋转中心,即平行四边形ABCD是中心对称图形;(2)根据平行四边形中对角、对边分别相等,∠B=∠ADC=60°,再根据已知边长,由勾股定理可求出AB、AD的长,进而可求出平行四边形ABCD的周长.
试题解析:1)∵四边形ABCD是平行四边形,
∴对角线互相平分,
∴O为旋转中心,
即平行四边形ABCD是中心对称图形,
(2)∵四边形ABCD是平行四边形,
∴∠B=∠D=60°,AB=CD,AD=BC.
∵AE⊥BC,
∵BE=4,
∴AB=8,
∴CD=AB=8,
∵CF=2,∴DF=6,
∵AF⊥DC,∠D=60°
∴在Rt△ADF中,AD=12,
∴平行四边形ABCD的周长=2(12+8)=40.
2、【解】 解:分别过点A作AM⊥BC于M,CN⊥AD于N,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=9 cm,
∴AM=CN,∵S AEFG=GF·AM,∴AM===4(cm),
∴CN=AM=4 cm,∵四边形AEFG是平行四边形,∴AE=GF=3 cm,
∴DE=6 cm,∴S△ABG=BG·AM=6(cm2),
S梯形CDEF=(CF+DE)·CN=18(cm2)
3、【解】 解:过点B作BM⊥AD,交DA的延长线于点M,过点C作CN⊥AD于点N,∵四边形ABCD是平行四边形,∴AD∥BC,∴AM=CN,∴S△ABP+S△PCD=AP·BM+DP·CN=AP·BM+DP·BM=BM(AP+DP)=AD·BM=S ABCD,∴S ABCD=2(S△ABP+S△PCD)=2(3+1)=8
4、【解】解:过点A作AG⊥n于点G,EH⊥n于点H,∵m∥n,
∴AG=EH,∵AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,又∵S△CEF=CF·EH=10,CD∶CF=2∶1,
∴S ABCD=CD·AG=2CF·EH=40
5、解:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∵AB∥CD,AE∥CF,∴AE=CF,∵AD∥BC,
AE∥CF,∴AG=CH,∴AE-AG=CF-CH,即EG=FH
6、解:设平行线AD,GH之间的距离为h1,
平行线GH,BC之间的距离为h2,则==
,==,∴=,
即=,∴S OEDH=24
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
