5.1多边形(1)[下学期]

课件36张PPT。5.1多边形（1）请欣赏图片! 并思考由下面这些图片你能抽象出什么几何图形？风　筝澳门:元荷兰:荷兰盾海地:古德缅甸:缅元由这些图片你能抽象出什么几何图形(平面的)？
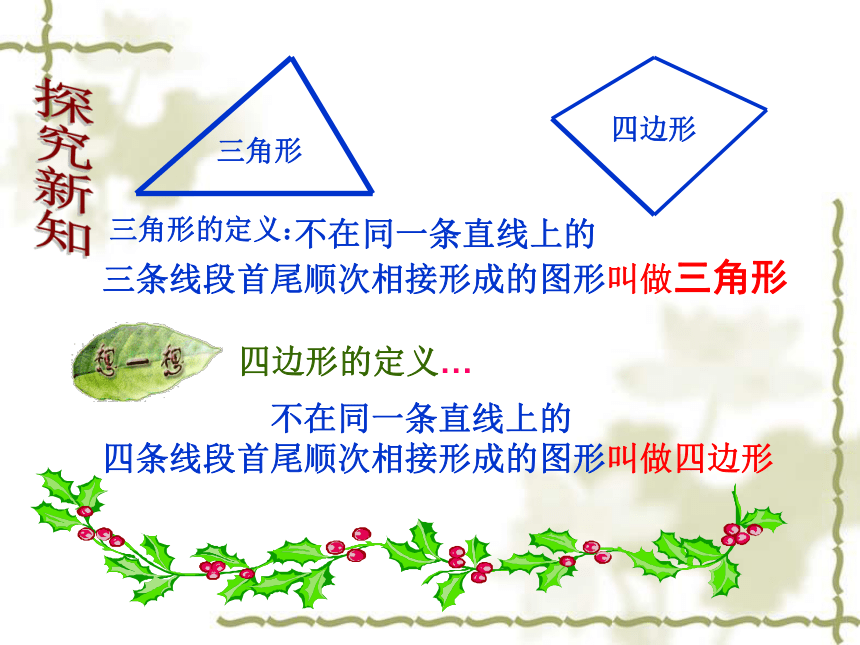
5.1多边形（1）探究新知 不在同一条直线上的
三条线段首尾顺次相接形成的图形叫做三角形　　　　　不在同一条直线上的
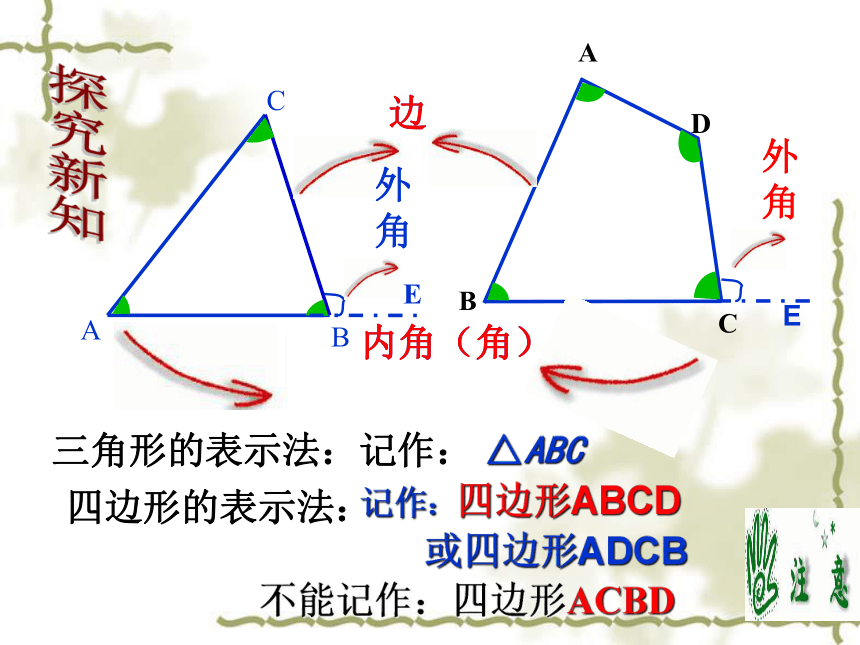
四条线段首尾顺次相接形成的图形叫做四边形三角形的定义：四边形的定义…探究新知AC内角（角）边内角（角）边四边形的表示法：
记作：四边形ABCD三角形的表示法：记作： △ABC
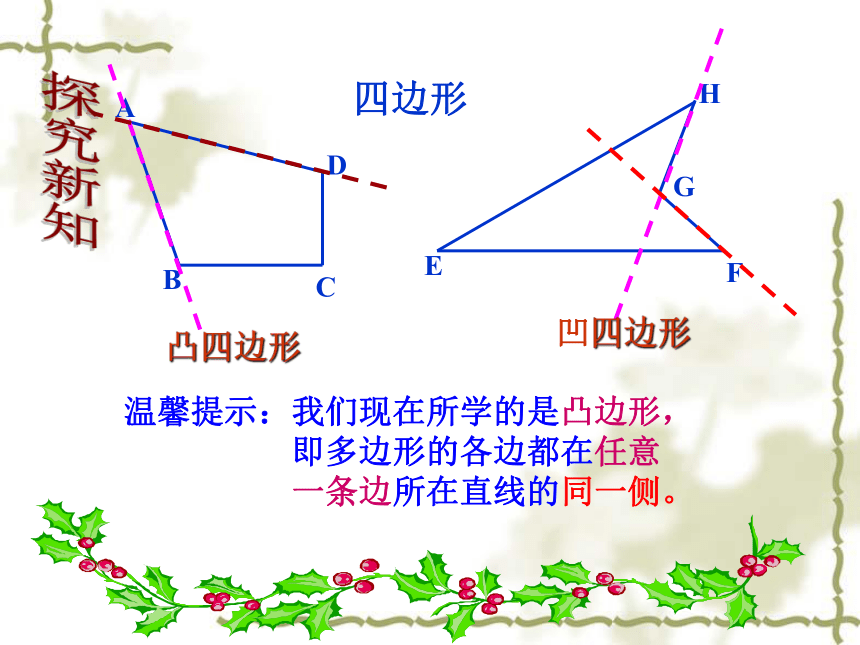
不能记作：四边形ACBDEE外角外角或四边形ADCB凸四边形凹四边形温馨提示：我们现在所学的是凸边形，
　　　　　即多边形的各边都在任意
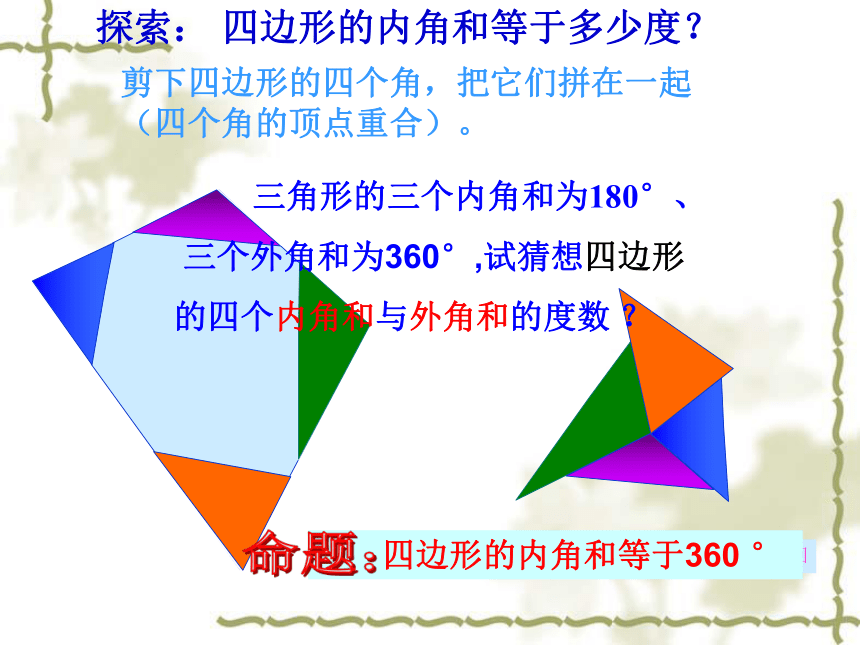
　　　　　一条边所在直线的同一侧。四边形探究新知剪下四边形的四个角，把它们拼在一起（四个角的顶点重合）。探索： 四边形的内角和等于多少度？ 三角形的三个内角和为180°、
三个外角和为360°,试猜想四边形
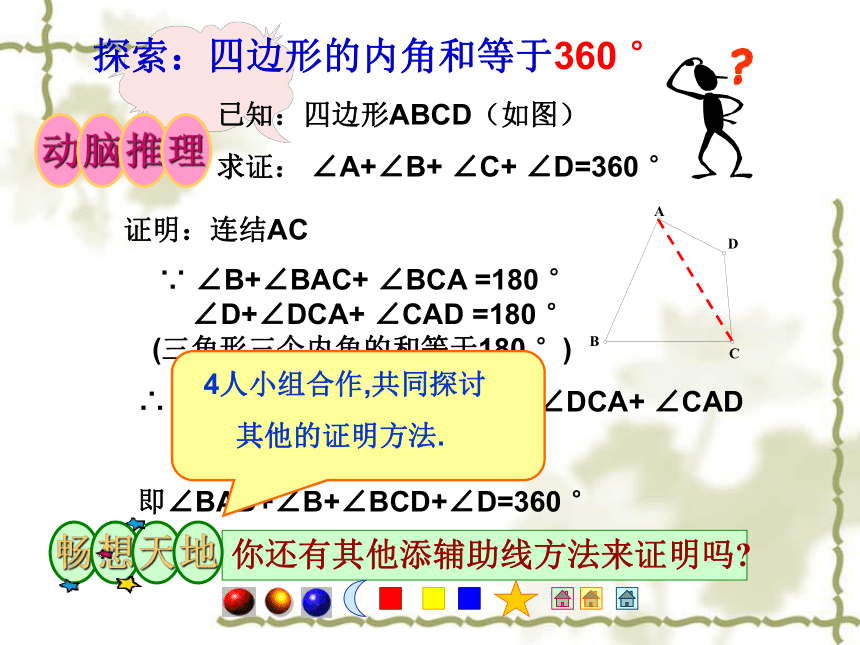
的四个内角和与外角和的度数 ？探索：四边形的内角和等于360 °
已知：四边形ABCD（如图）
求证： ∠A+∠B+ ∠C+ ∠D=360 °证明：连结AC ∵ ∠B+∠BAC+ ∠BCA =180 °
∠D+∠DCA+ ∠CAD =180 °
(三角形三个内角的和等于180 °)∴ ∠B+∠BAC+ ∠BCA+ ∠D+∠DCA+ ∠CAD
=180 °+ 180° = 360°即∠BAD+∠B+∠BCD+∠D=360 °∴∠BAC+∠B+∠C＝∠BAC+∠BAD+∠CAE
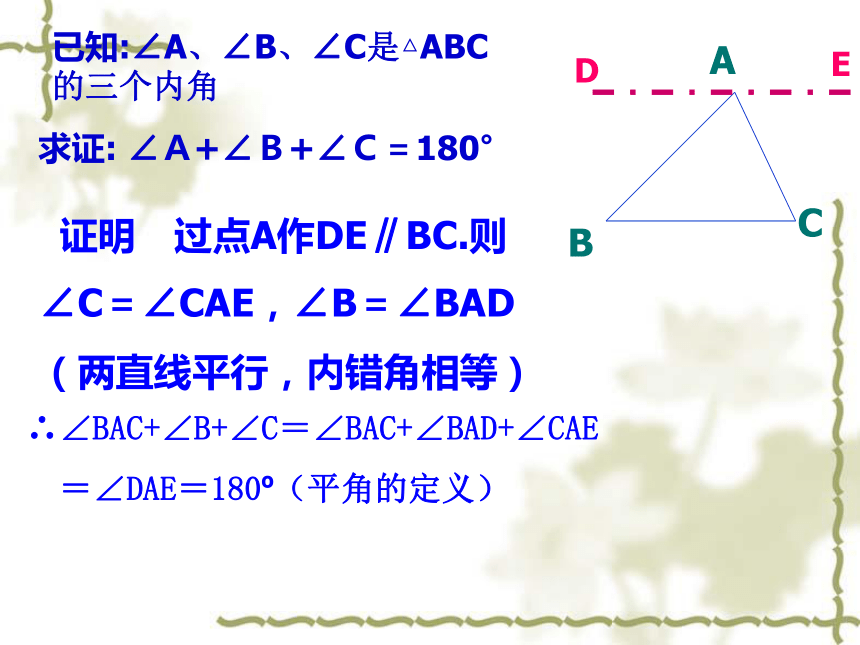
　＝∠DAE＝180o（平角的定义）ACBDE证明　过点A作DE∥BC.则∠C＝∠CAE，∠B＝∠BAD
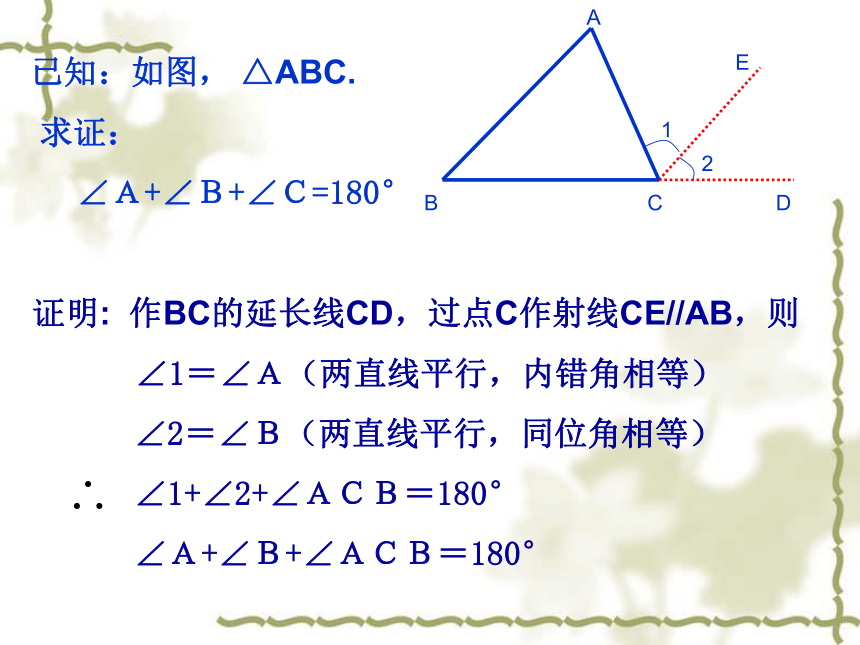
（两直线平行，内错角相等）已知:∠A、∠B、∠C是△ABC的三个内角求证: ∠Ａ+∠Ｂ+∠Ｃ＝180°证明: 作BC的延长线CD，过点C作射线CE//AB，则
∠1＝∠Ａ（两直线平行，内错角相等）
∠2＝∠Ｂ（两直线平行，同位角相等）
∠1+∠2+∠ＡＣＢ＝180°
∠Ａ+∠Ｂ+∠ＡＣＢ＝180°畅想天地探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=3个三角形的内角和－1个平角
=3×180°－180° =360°· O 证明思路：
四边形的内角和=4个三角形的内角和一1个周角
=4×180°－360° =360°畅想天地探索： 四边形的内角和等于360 °
探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=3个三角形的内角和一1个三角形的内角和
=3×180°－180° =360°畅想天地探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=2个三角形的内角和+1对同旁内角和
　　　　一2个直角 =2×180°+ 180° －180 =360°畅想天地探索： 四边形的内角和等于360 °
E过点D作DE∥BC 证明思路：
四边形的内角和=1个三角形的内角和+2对同旁内角的和
一1个平角 =180°+2× 180° －180° =360°畅想天地探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=2个平角+1个三角形的内角和一1个三
角形的内角和
=2×180°+ 180° －180° =360°畅想天地=2个平角=2×180=360°
探索： 四边形的内角和等于360 °
证明思路：
四边形的内角和=4个三角形的内角和一1个周角
=4×180°－360° =360°O。畅想天地探索： 四边形的内角和等于360 °
E 证明思路：
四边形的内角和=1个周角=360°畅想天地探索： 四边形的内角和等于360 °
EF 证明思路：
四边形的内角和=2个三角形的内角和=2×180° =360°畅想天地探索： 四边形的内角和等于360 °
探索： 四边形的内角和等于360 °
EABC2134 在每个顶点处取这个四边形的一个外角，它们的和叫做这个四边形的外角和。 解 :∵∠ 1+∠5 =∠2+ ∠6= ∠3+∠7= ∠ 4+∠8= 180°
猜想：四边形的外角和等于多少度？即:∠ 1＋∠ 2+ ∠3 +∠4 =？推论：四边形的外角和等于360°5678
∵ ∠5 +∠ 6 + ∠ 7 +∠8=360°(四边形的内角和是360°)
∴ ∠1 +∠ 2 + ∠ 3 +∠4 = 720°－ 360°= 360°∴ ∠ 1+∠5 +∠2+ ∠6+ ∠3+∠7+ ∠ 4+∠8
= 4× 180°= 720° 即: (∠ 1+∠2 +∠ 3 + ∠4)+ (∠5 +∠ 6+ ∠ 7 +∠8) = 720°妞妞原先站在A处面朝B。按逆时针方向走一
圈回到A处，然后转一个角度 ∠ 1 使面仍朝B。想一想⑴妞妞在每一次转弯时,
身体转过的角是哪个角？⑵她每跑完一圈，身体
转过的角度之和是多少？⑶这也验证了四边形的什么定理？想一想 妞妞原先站在A处面朝B。按逆时针方向走一
圈回到A处，然后转一个角度 ∠ 1 使面仍朝B。⑴妞妞在每一次转弯时,身体转过的角是哪个角？⑵她每跑完一圈，身体转过的角度之和是多少？⑶这也验证了四边形的什么定理？

想一想四边形的外角和等360° 妞妞原先站在A处面朝B。按逆时针方向走一
圈回到A处，然后转一个角度 ∠ 1 使面仍朝B。⑴妞妞在每一次转弯时,身体转过的角是哪个角？⑵她每跑完一圈，身体转过的角度之和是多少？⑶这也验证了四边形的什么定理？现学现用1.已知四边形ABCD中， ∠A＝80 °, ∠B＝60°, ∠C=70°则∠D=_____.体 验 成 功150 °128 °109°56 °100° 小A家准备用一批大小，形状一样的(全等)四边形木板来密铺（不留空隙,不重叠的铺成一片）地板,你认为可以用这些全等的四边形来密铺地板吗?生活大探秘用你们手中的纸片摆一摆,试试看?这是利用了四边形的什么性质呢？（同桌合作）四边形的内角和等于360°
我最感兴趣的地方是……这节课我的收获是……
我想进一步研究的问题是……大家说:4.已知:在四边形ABCD中, ∠A=∠C=900. BE平分∠ABC,交CD于点E,DF平分∠ADC,交AB于点F. 求证:BE∥DF.2EF3411．一个定义，一个定理，一个推论
2．重要数学方法三角形的概念 四边形的概念

四边形问题 三角形问题类比转化（已知）（未知）类比转化（未知）（已知）小结⑵必做题:
作业本(1) 及书本作业题。
作业⑴思考题:
① 探索五边形,六边形, ……, n边形的内角和、外角和,你能否发现并找出n边形的内角和与外角和的计算规律吗?
②生活中,四边形可以用来密铺平面,其它多边形可以吗?密铺的数学原理是什么?
鸟儿因为翅膀而飞翔风筝因为风儿而飞翔人类因为思考而飞翔让我们一起想象，
让我们一起飞翔！再见