有理数的加法(一)(浙江省杭州市西湖区)
文档属性
| 名称 | 有理数的加法(一)(浙江省杭州市西湖区) |  | |
| 格式 | rar | ||
| 文件大小 | 594.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-07-02 17:14:00 | ||
图片预览


文档简介
课件17张PPT。 阿贝尔留下的可以使数学家忙碌五百年。 -----埃尔米特
(C. Hermice 1822 – 1901) 2.1有理数的加法
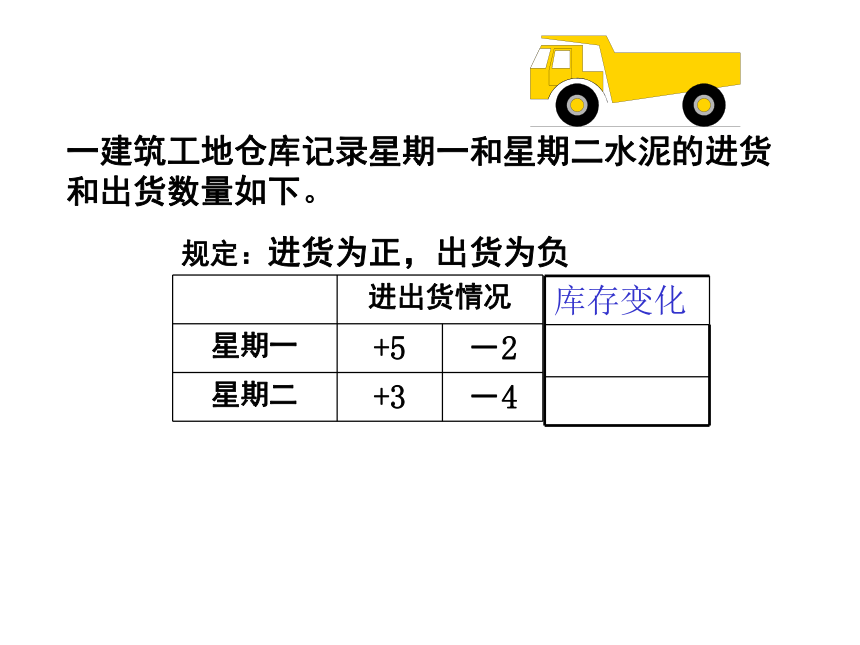
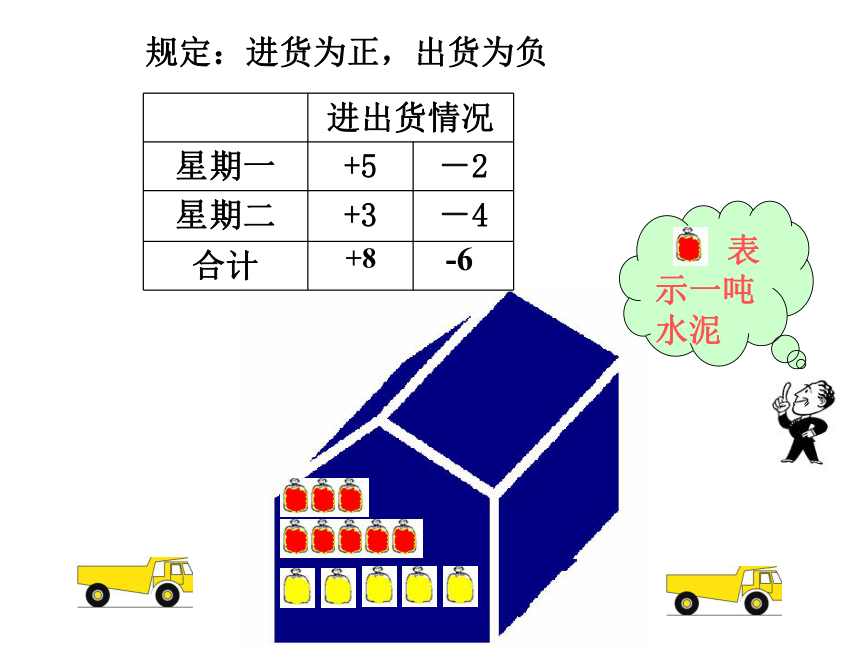
第一课时规定:进货为正,出货为负一建筑工地仓库记录星期一和星期二水泥的进货和出货数量如下。 表示一吨水泥 规定:进货为正,出货为负+8-6有 (+5)+(+3)=+8
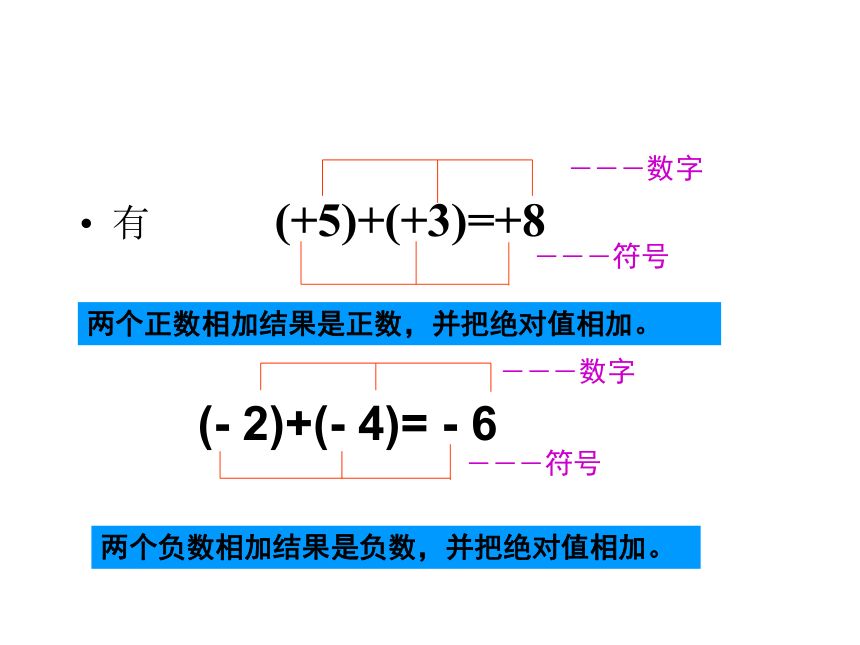
两个正数相加结果是正数,并把绝对值相加。 (- 2)+(- 4)= - 6两个负数相加结果是负数,并把绝对值相加。---数字---符号---数字---符号确定下列各题中和的符号,并说明理由.
(1)(+5)+(+7);
(2)(-10)+(-3);
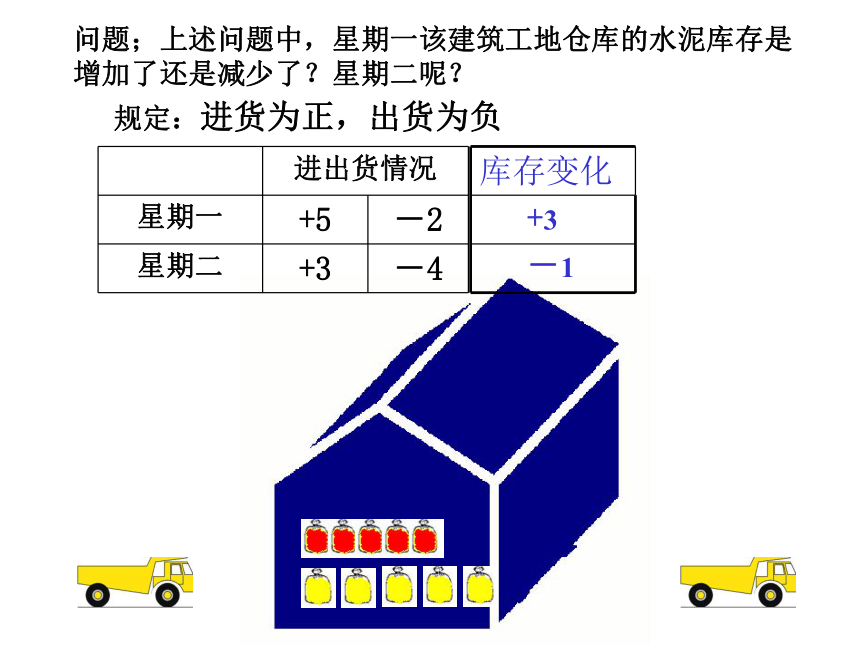
(3)(+6)+(-5); 试一 试 规定:进货为正,出货为负-1+3问题;上述问题中,星期一该建筑工地仓库的水泥库存是增加了还是减少了?星期二呢?
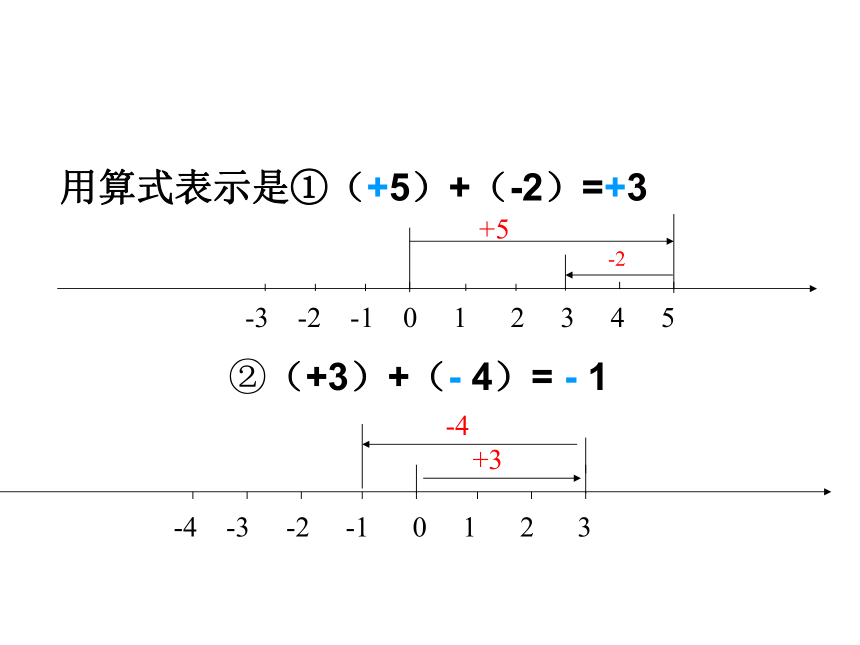
用算式表示是①(+5)+(-2)=+3
+5-2 -4 -3 -2 -1 0 1 2 3 -4+3②(+3)+(- 4)= - 1
有理数的加法 同号两数相加,取与加数相同的符号,并把绝对值相加.
异号两数相加,取与绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零;一个数同零相加仍得这个数.
一起说一说有理数加法运算的步骤:
先确定结果的符号,再计算结果的绝对值。确定下列各题中的符号,并说明理由:
(1)(+5)+(+7);
(2)(-3)+(-10);
(3)(+6)+(—5);
(4)(+3)+(-7);
(5)(- )+(+ );
(6) 0+(- );
——+ —0 + 一起算一算(1)(-11)+(-9) (2)(-3.5)+(+7)
(3)(-1.08)+0 (4)( + )+(- )(11+9)解:(1) (-11)+(-9)== -20-确定符号确定绝对值过关斩将 (+7.3)+(+3.7)
(-42)+(+17)
0+(-39.98)
计算下列各题 老板派了甲、乙、丙、丁辆车向四个地方运送水泥. 如果规定向东为正,向西为负,你能算出它们最后停在哪里吗?过关斩将甲:从仓库出发,先向东 行驶 2 千米,
再向东 行驶 3 千米;
乙:从仓库出发,先向东 行驶 2 千米,
再向西 行驶 3 千米;
丙:从仓库出发,先向西 行驶 3 千米,
再向西 行驶 2 千米;
丁:从仓库出发,先向西 行驶 5 千米,
再向东 行驶 4 千米.规定以仓库为原点,向东为正方向,向西为负方向. 甲:从仓库出发,先向东行驶2千米,再向东行驶3千米. 乙:从仓库出发,先向东行驶2千米,再向西行驶3千米.你能利用数轴上求得丙与丁最后停在哪里吗?
过关斩将三 丙:从仓库出发,先向 西 行驶 3 千米,
再向 西 行驶 2 千米;
丁:从仓库出发,先向 西 行驶 5 千米,
再向 东 行驶 4 千米.
1、下列两个有理数相加:①两个正数;②两个负数;③一正一负,但正数的绝对值较大;④一正一负,但正数的绝对值较小;⑤零与正数;⑥零与负数;那么,
(1)和为正数的是(填入代号,下同) ;
(2)和为负数的是 ;
(3)和的绝对值等于加数绝对值的和的是 ;
(4)和的绝对值等于加数中较大绝对值与较小绝对值的差的是 ;
(5)和等于其中一个加数的是 ;
2、两个有理数相加,和是否一定大于每一个加数?请举例说明。 ① ③ ⑤② ④ ⑥① ② ⑤ ⑥③ ④ ⑤ ⑥⑤ ⑥练一练:2. 在括号里填上适当的符号,使下列式子成立:
(1) ( 5) + ( 5) = 0
(2) ( 7) + ( - 5 ) = -12
(3) ( -10 ) + ( 11) = +1
(4) ( 2.5) + ( 2.5) = -5 +--+--作业:1。作业本,2。每课一练
3。课本P26作业题 2.根据
编一道应用题.算式:-45+30=-15
(C. Hermice 1822 – 1901) 2.1有理数的加法
第一课时规定:进货为正,出货为负一建筑工地仓库记录星期一和星期二水泥的进货和出货数量如下。 表示一吨水泥 规定:进货为正,出货为负+8-6有 (+5)+(+3)=+8
两个正数相加结果是正数,并把绝对值相加。 (- 2)+(- 4)= - 6两个负数相加结果是负数,并把绝对值相加。---数字---符号---数字---符号确定下列各题中和的符号,并说明理由.
(1)(+5)+(+7);
(2)(-10)+(-3);
(3)(+6)+(-5); 试一 试 规定:进货为正,出货为负-1+3问题;上述问题中,星期一该建筑工地仓库的水泥库存是增加了还是减少了?星期二呢?
用算式表示是①(+5)+(-2)=+3
+5-2 -4 -3 -2 -1 0 1 2 3 -4+3②(+3)+(- 4)= - 1
有理数的加法 同号两数相加,取与加数相同的符号,并把绝对值相加.
异号两数相加,取与绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
互为相反数的两个数相加得零;一个数同零相加仍得这个数.
一起说一说有理数加法运算的步骤:
先确定结果的符号,再计算结果的绝对值。确定下列各题中的符号,并说明理由:
(1)(+5)+(+7);
(2)(-3)+(-10);
(3)(+6)+(—5);
(4)(+3)+(-7);
(5)(- )+(+ );
(6) 0+(- );
——+ —0 + 一起算一算(1)(-11)+(-9) (2)(-3.5)+(+7)
(3)(-1.08)+0 (4)( + )+(- )(11+9)解:(1) (-11)+(-9)== -20-确定符号确定绝对值过关斩将 (+7.3)+(+3.7)
(-42)+(+17)
0+(-39.98)
计算下列各题 老板派了甲、乙、丙、丁辆车向四个地方运送水泥. 如果规定向东为正,向西为负,你能算出它们最后停在哪里吗?过关斩将甲:从仓库出发,先向东 行驶 2 千米,
再向东 行驶 3 千米;
乙:从仓库出发,先向东 行驶 2 千米,
再向西 行驶 3 千米;
丙:从仓库出发,先向西 行驶 3 千米,
再向西 行驶 2 千米;
丁:从仓库出发,先向西 行驶 5 千米,
再向东 行驶 4 千米.规定以仓库为原点,向东为正方向,向西为负方向. 甲:从仓库出发,先向东行驶2千米,再向东行驶3千米. 乙:从仓库出发,先向东行驶2千米,再向西行驶3千米.你能利用数轴上求得丙与丁最后停在哪里吗?
过关斩将三 丙:从仓库出发,先向 西 行驶 3 千米,
再向 西 行驶 2 千米;
丁:从仓库出发,先向 西 行驶 5 千米,
再向 东 行驶 4 千米.
1、下列两个有理数相加:①两个正数;②两个负数;③一正一负,但正数的绝对值较大;④一正一负,但正数的绝对值较小;⑤零与正数;⑥零与负数;那么,
(1)和为正数的是(填入代号,下同) ;
(2)和为负数的是 ;
(3)和的绝对值等于加数绝对值的和的是 ;
(4)和的绝对值等于加数中较大绝对值与较小绝对值的差的是 ;
(5)和等于其中一个加数的是 ;
2、两个有理数相加,和是否一定大于每一个加数?请举例说明。 ① ③ ⑤② ④ ⑥① ② ⑤ ⑥③ ④ ⑤ ⑥⑤ ⑥练一练:2. 在括号里填上适当的符号,使下列式子成立:
(1) ( 5) + ( 5) = 0
(2) ( 7) + ( - 5 ) = -12
(3) ( -10 ) + ( 11) = +1
(4) ( 2.5) + ( 2.5) = -5 +--+--作业:1。作业本,2。每课一练
3。课本P26作业题 2.根据
编一道应用题.算式:-45+30=-15
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
