3.8 弧长公式第1课时

课件18张PPT。3.8 弧长及扇形的面积第1课时 弧长公式做一做1.已知圆的半径为10CM，求：
（1）半圆的弧长.
（2）90°圆心角所对的弧长.
（3）1°圆心角所对的弧长.
（4）60°圆心角所对的弧长.
2.已知圆的半径为R，
求n°圆心角所对的弧长L.
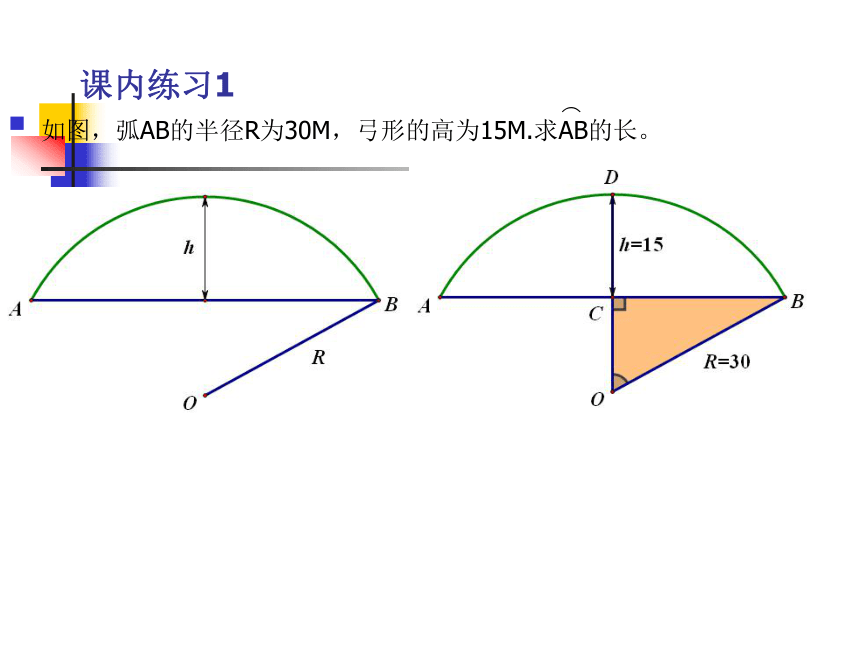
课内练习1如图，弧AB的半径R为30M，弓形的高为15M.求AB的长。
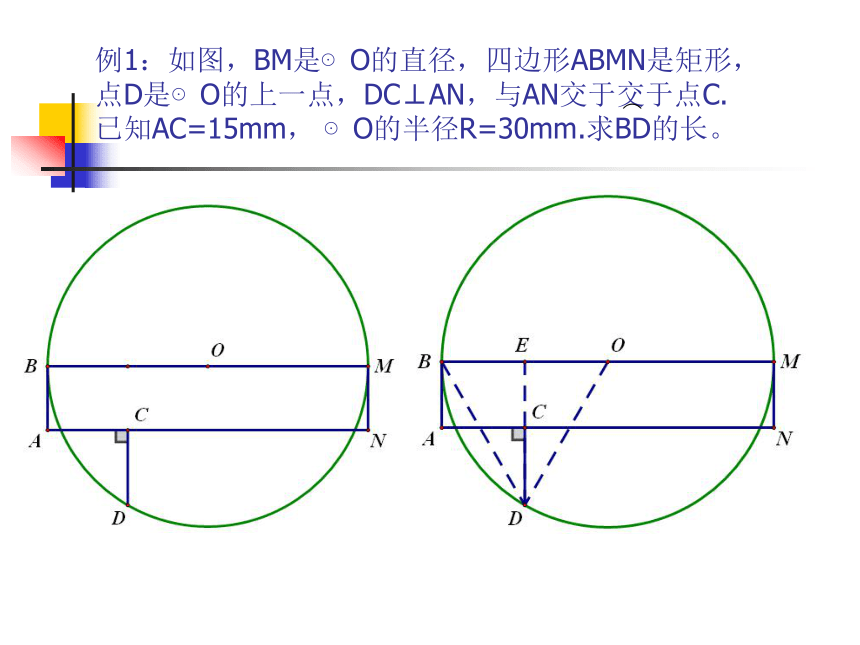
⌒例1：如图，BM是⊙O的直径，四边形ABMN是矩形，点D是⊙O的上一点，DC⊥AN，与AN交于交于点C.已知AC=15mm， ⊙O的半径R=30mm.求BD的长。⌒填 一 填
1．圆周长公式
公式：圆周长l＝_________.
2．弧长计算公式【知识管理】2πR
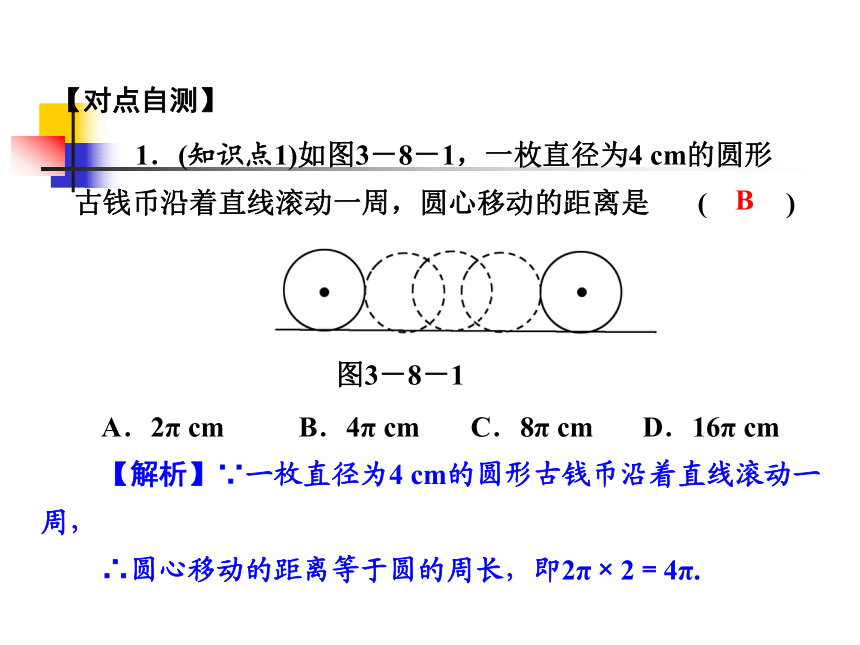
1．(知识点1)如图3－8－1，一枚直径为4 cm的圆形古钱币沿着直线滚动一周，圆心移动的距离是 (　 　)【对点自测】图3－8－1A．2π cm　 B．4π cm　 C．8π cm　 D．16π cm
【解析】∵一枚直径为4 cm的圆形古钱币沿着直线滚动一周，
∴圆心移动的距离等于圆的周长，即2π×2＝4π.B2．(知识点2)弧长计算公式是 (　 　)3．(知识点2)一个扇形的圆心角为90°.半径为2，则这个扇形的弧长为______.(结果保留π)Aπ4．(知识点2)已知一弧长为20π cm，其所对圆心角为150°，则此弧所在圆的半径为_______cm.24研 一 研类型之一　利用弧长公式求弧长
例1　已知扇形的圆心角为120°，半径为30 cm，则扇形的弧长为_______cm(结果保留π)．2π图3－8－22．已知圆上一段弧长为5π cm，它所对的圆心角为100°，则该圆的半径为 (　 　)
A．6 cm　　　　　　 　 B．9 cm
C．12 cm D．18 cmB3．一定滑轮的起重装置如图3－8－3，滑轮半径为12 cm，当重物上升4π cm时，滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动) (　 　)图3－8－3A．12° B．30°
C．60° D．90°C类型之二　滚动物体的弧长计算 图3－8－4 1．在Rt△ABC中，∠C＝90°，BC＝4 cm，AC＝3 cm.把△ABC绕点A顺时针旋转90°后，得到△AB1C1(如图3－8－5所示)，则点B所走过的路径长为(　 　)图3－8－5C图3－8－63．如图3－8－7所示，在Rt△ABC中，∠BAC＝90°，BC＝6，点D为BC中点，将△ABD绕点A按逆时针方向旋转120°得到△AB′D′，则点D在旋转过程中所经过的路线长为_______.图3－8－72π