第1章 二次函数单元经典题型检测卷(含解析)
文档属性
| 名称 | 第1章 二次函数单元经典题型检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 813.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 16:48:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1章 二次函数 单元经典题型检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B. C.y=(x+2)(x+1)﹣x2 D.y=2x2+3x
2.抛物线y=3(x﹣2)2+1的顶点坐标是( )
A.(2,1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
3.抛物线y=﹣3(x﹣4)2﹣5的最大值为( )
A.4 B.﹣4 C.5 D.﹣5
4.已知抛物线y=x2+mx的对称轴为直线x=2,则m的值是( )
A.4 B.2 C.﹣2 D.﹣4
5.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
6.已知抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,则方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为( )
A.x1=x2=2 B.x1=﹣1,x2=3 C.x1=0,x2=4 D.x1=﹣2,x2=2
7.如图,李大爷用24米长的篱笆靠墙围成一个长方形(ABCD)菜园,若菜园靠墙的一边(AD)长为x(米),那么菜园的面积y(平方米)与x的关系式为( )
A. B.y=x(12﹣x) C. D.y=x(24﹣x)
8.在平面直角坐标系中,将二次函数y=(x+1)2的图象关于x轴对称后,再向下平移2个单位长度所得抛物线对应的函数表达式为( )
A.y=(x+1)2﹣2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x+1)2+2
9.若函数y=x2﹣2x﹣m与x轴没有交点,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限.
A.一 B.二 C.三 D.四
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2﹣4ac>0,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分24分,每小题4分)
11.如果函数+3是二次函数,则m的值为 .
12.若抛物线y=﹣x2+4x﹣n的顶点在x轴的下方,则实数n的取值范围是 .
13.已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … ﹣5 0 3 4 3 m ﹣5 …
根据表格内容,该二次函数的m值为 .
14.已知点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,如果MN∥x轴,那么点N的坐标为 .
15.某种型号的小型无人机着陆后滑行的距离S(米)关于滑行的时间t(秒)的函数解析式是S=﹣0.25t2+8t,无人机着陆后滑行 秒才能停下来.
16.已知直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,则b取值范围是 .
三.解答题(共7小题,满分66分)
17.(6分)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=﹣2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
18.(6分)在如图所示的平面直角坐标系中,画出y=x2﹣4x+3的图象.
19.(8分)已知二次函数的图象经过A(0,﹣6)、B(﹣1,﹣5)、C(m,m)三点.
(1)若点A为该函数图象的顶点,求二次函数的表达式;
(2)若该函数图象的对称轴为直线x=﹣3,求m的值;
(3)若a>0,当﹣1<x<0时,y随x的增大而减小.结合图象,直接写出m的取值范围.
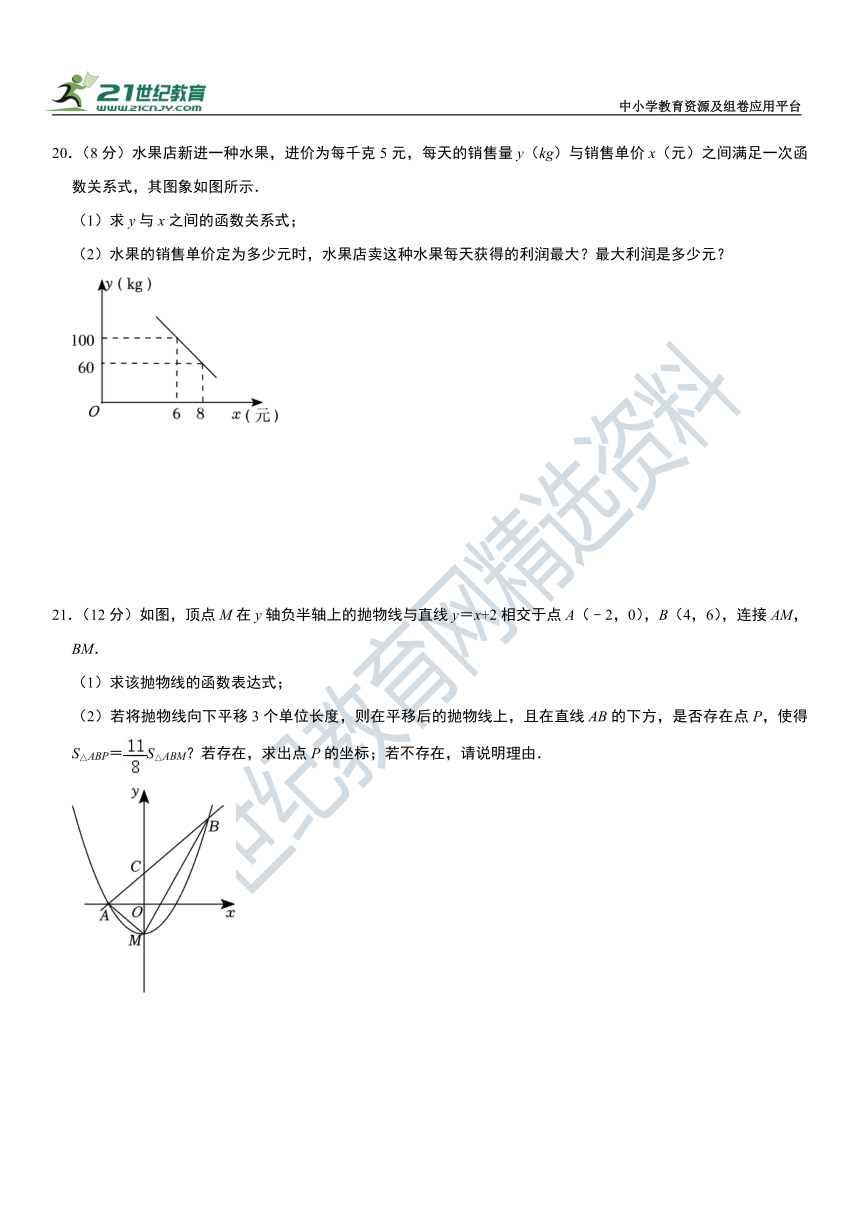
20.(8分)水果店新进一种水果,进价为每千克5元,每天的销售量y(kg)与销售单价x(元)之间满足一次函数关系式,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)水果的销售单价定为多少元时,水果店卖这种水果每天获得的利润最大?最大利润是多少元?
21.(12分)如图,顶点M在y轴负半轴上的抛物线与直线y=x+2相交于点A(﹣2,0),B(4,6),连接AM,BM.
(1)求该抛物线的函数表达式;
(2)若将抛物线向下平移3个单位长度,则在平移后的抛物线上,且在直线AB的下方,是否存在点P,使得S△ABP=S△ABM?若存在,求出点P的坐标;若不存在,请说明理由.
22.(12分)如图是一个东西走向近似于抛物线的山坡,以地面的东西方向为x轴、西侧的坡底为原点建立平面直角坐标系,山坡近似满足函数表达式y=﹣x,无人机从西侧距坡底O为10米处的B点起飞,沿山坡由西向东飞行,飞行轨迹近似满足抛物线y=﹣x2+bx+c,当无人机飞越坡底上空时(即点D,与地面的距离为20米.
(1)求无人机飞行轨迹的函数表达式,并写出自变量x的取值范围;
(2)当无人机飞行的水平距离距起点为30米时,求无人机与山坡的竖直距离d;
(3)由于山坡上有障碍物,无人机不能离山坡过近.当无人机与山坡的竖直距离大于9米时,无人机飞行才是安全的,请判断无人机此次飞行是否安全,并说明理由.
23.(14分)如图,抛物线y=ax2+4x+c与直线y=﹣x+5交x轴于点A,交y轴于点B.
(1)求抛物线的解析式,并求出当﹣2≤x≤3时,y的取值范围;
(2)抛物线与x轴另一交点为E,连接BE,在抛物线上是否存在点F,使得∠ABF=∠ABE,若存在请求出点F的坐标,若不存在说明理由.
(3)如图2,以AB为边作矩形ABCD,设点C的横坐标为m.当CD边与抛物线只有一个公共点时,请直接写出m的取值范围.
第1章 二次函数 单元经典题型检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B.
C.y=(x+2)(x+1)﹣x2 D.y=2x2+3x
【分析】根据二次函数的一般形式:形如y=ax2+bx+c(a,b,c为常数且a≠0),逐一判断即可解答.
【解答】解:A、y=(a+2)x2+1(a≠﹣2),是二次函数,故A不符合题意;
B、y=+1,不是二次函数,故B不符合题意;
C、y=(x+2)(x+1)﹣x2=3x+2,是一次函数,故C不符合题意;
D、y=2x2+3x,是二次函数,故D符合题意;
故选:D.
2.抛物线y=3(x﹣2)2+1的顶点坐标是( )
A.(2,1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
【分析】直接由抛物线解析式可求得答案.
【解答】解:∵y=3(x﹣2)2+1,
∴抛物线顶点坐标为(2,1),
故选:A.
3.抛物线y=﹣3(x﹣4)2﹣5的最大值为( )
A.4 B.﹣4 C.5 D.﹣5
【分析】所给抛物线是顶点式,可直接得出抛物线的对称轴.
【解答】解:∵抛物线y=a(x+h)2+k的最大值是k,
∴抛物线y=﹣3(x﹣4)2﹣5的最大值为﹣5.
故选:D.
4.已知抛物线y=x2+mx的对称轴为直线x=2,则m的值是( )
A.4 B.2 C.﹣2 D.﹣4
【分析】根据二次函数对称轴的公式即可求解.
【解答】解:y=x2+mx,
∴对称轴为直线x==2,
解得m=﹣4,
故选:D.
5.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
【分析】利用对称轴x=﹣,左同右异判断对称轴位置,结合一次函数图象走向与二次函数开口方向逐个判断即可.
【解答】解:A,结合图象y=mx﹣n中,m>0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣<0,与图象不符,不符合题意;
B,结合图象y=mx﹣n中,m>0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣<0,图象没过原点,与图象不合,不符合题意;
C,结合图象y=mx﹣n中,m>0,n<0,此时二次函数y=mx2+nx中对称轴x=﹣>0,与图象不符,不符合题意;
D,结合图象y=mx﹣n中,m<0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣>0与图象符合,符合题意;
故选:D.
6.已知抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,则方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为( )
A.x1=x2=2 B.x1=﹣1,x2=3 C.x1=0,x2=4 D.x1=﹣2,x2=2
【分析】先将方程(x﹣1)2+m2=2m(x﹣1)﹣n化简,再根据抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点和二次函数图象平移的特点,即可写出抛物线y=(x﹣m﹣1)2+n与x轴交于(0,0)、(4,0)两点,然后即可得到方程(x﹣1)2+m2=2m(x﹣1)﹣n的解.
【解答】解:(x﹣1)2+m2=2m(x﹣1)﹣n,
化简,得:(x﹣m﹣1)2+n=0,
∵抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,
∴抛物线y=(x﹣m﹣1)2+n与x轴交于(0,0)、(4,0)两点,
∴方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为x1=0,x2=4,
故选:C.
7.如图,李大爷用24米长的篱笆靠墙围成一个长方形(ABCD)菜园,若菜园靠墙的一边(AD)长为x(米),那么菜园的面积y(平方米)与x的关系式为( )
A. B.y=x(12﹣x) C. D.y=x(24﹣x)
【分析】根据AD的边长为x米,可以得出AB的长为米,然后根据矩形的面积公式即可求出函数关系式.
【解答】解:∵AD的边长为x米,而菜园ABCD是矩形菜园,
∴AB=米,
∵菜园的面积=AD×AB=x ,
∴y=.
故选:C.
8.在平面直角坐标系中,将二次函数y=(x+1)2的图象关于x轴对称后,再向下平移2个单位长度所得抛物线对应的函数表达式为( )
A.y=(x+1)2﹣2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x+1)2+2
【分析】直接利用关于x对称的点横坐标不变,纵坐标互为相反数得到关于x轴对称后的解析式,进而利用上下平移规律得出答案.
【解答】解:将二次函数y=(x+1)2的图象关于x轴对称后,得抛物线解析式为:﹣y=(x+1)2,即y=﹣(x+1)2,再向下平移2个单位长度所得抛物线对应的函数表达式是:y=﹣(x+1)2﹣2.
故选:C.
9.若函数y=x2﹣2x﹣m与x轴没有交点,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限.
A.一 B.二 C.三 D.四
【分析】由二次函数y=x2﹣2x﹣m与x轴没有交点,可知Δ<0,得出m<﹣1,然后根据m的取值判定m+1,m﹣1的取值即可.
【解答】解:∵二次函数y=x2﹣2x﹣m与x轴没有交点,
∴Δ<0,即4+4m<0,
∴m<﹣1,
∴m+1<0,m﹣1<0,
一次函数经过二、三、四象限,不经过第一象限.
故选:A.
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2﹣4ac>0,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线开口方向得到a<0以及函数经过原点即可判断①,根据x=1时的函数值可以判断②;由抛物线的对称轴方程得到为b=2a<0,以及a的符号即可判断③;根据抛物线与x轴交点个数得到Δ=b2﹣4ac>0,则可对④进行判断.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线经过原点,
∴c=0,
则abc=0,所以①正确;
当x=1时,函数值是a+b+c<0,则②错误;
∵抛物线的对称轴为直线x=﹣=﹣<0,
∴b=3a<0,
又∵a<0,
∴a>b,则③正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以④正确.
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
11.如果函数+3是二次函数,则m的值为 2 .
【分析】由二次函数的定义进行计算,即可得到答案.
【解答】解:∵是二次函数,
∴,
解得:,
∴m=2;
故答案为:2.
12.若抛物线y=﹣x2+4x﹣n的顶点在x轴的下方,则实数n的取值范围是 n>4 .
【分析】先根据函数解析式得出抛物线的开口向下,根据顶点在x轴的下方得出Δ<0,求出即可.
【解答】解:∵抛物线y=﹣x2+4x﹣n的开口向下,顶点在x轴的下方,
而与x轴没有交点,
方程﹣x2+4x﹣n=0无实数根,
即b2﹣4ac=16﹣4n<0,
∴n>4.
故答案为:n>4.
13.已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … ﹣5 0 3 4 3 m ﹣5 …
根据表格内容,该二次函数的m值为 0 .
【分析】由表格个可得抛物线对称轴,再由抛物线对称性求解.
【解答】解:由表格可得抛物线经过(﹣2,3),(0,3),
∴抛物线对称轴为直线x=﹣1,
∴(﹣3,0),(1,m)关于对称轴对称,
∴m=0,
故答案为:0.
14.已知点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,如果MN∥x轴,那么点N的坐标为 (3,2) .
【分析】根据抛物线的对称性即可求得点N的坐标.
【解答】解:∵抛物线y=x2﹣2x+c,
∴抛物线的对称轴为直线x=﹣=1,
∵点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,且MN∥x轴,
∴M、N关于直线x=1对称,
∴点N的坐标为(3,2).
故答案为:(3,2).
15.某种型号的小型无人机着陆后滑行的距离S(米)关于滑行的时间t(秒)的函数解析式是S=﹣0.25t2+8t,无人机着陆后滑行 16 秒才能停下来.
【分析】飞机停下时,也就是滑行距离最远时,即在本题中需求出s最大时对应的t值.
【解答】解:由题意得,
S=﹣0.25t2+8t
=﹣0.25(t2﹣32t+256﹣256)
=﹣0.25(t﹣16)2+64,
∵﹣0.25<0,
∴t=16时,飞机滑行的距离最大,
即当t=16秒时,飞机才能停下来.
故答案为:16.
16.已知直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,则b取值范围是 ﹣1<b≤3 .
【分析】画出y=x2﹣4|x|+3图象即可求解.
【解答】解:根据描点法画出y=x2﹣4|x|+3图象,如图所示,
若直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,
由图象可得:﹣1<b≤3,
故答案为:﹣1<b≤3.
三.解答题(共7小题,满分66分)
17.(6分)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=﹣2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
【分析】(1)把x=3,y=3代入y=ax2求出a,得到这个二次函数的表达式,再将x=﹣2代入即可求出y的值;
(2)根据a的符号判断抛物线的开口方向,把抛物线解析式化为顶点式,进而求出对称轴、顶点坐标.
【解答】解:(1)把x=3,y=3代入y=ax2得,
a 32=3,解得a=,
所以这个二次函数的表达式为y=x2;
当x=﹣2时,y=×(﹣2)2=;
(2)∵y=x2,a=>0,
∴图象开口向上;
对称轴是直线x=0,顶点坐标是(0,0).
18.(6分)在如图所示的平面直角坐标系中,画出y=x2﹣4x+3的图象.
【分析】根据函数解析式,求出对称轴、交点坐标与y轴交点坐标,用平滑的曲线连接即可.
【解答】解:由题意可知,
y=x2﹣4x+3与x轴的交点坐标为(1,0)和(3,0),与y轴的交点为(0,3),
对称轴为x===2,
顶点坐标为(2,﹣1),
如图,
.
19.(8分)已知二次函数的图象经过A(0,﹣6)、B(﹣1,﹣5)、C(m,m)三点.
(1)若点A为该函数图象的顶点,求二次函数的表达式;
(2)若该函数图象的对称轴为直线x=﹣3,求m的值;
(3)若a>0,当﹣1<x<0时,y随x的增大而减小.结合图象,直接写出m的取值范围.
【分析】(1)先设抛物线的顶点式,再代入求解;
(2)先设抛物线的顶点式,再求出解析式,再求出当x=y时的x值;
(3)由题意得:抛物线的对称轴为:x≥0,结合图象求解.
【解答】解:(1)设二次函数的解析式为:y=ax2﹣6,
由题意得:a﹣6=﹣5,
解得:a=1,
∴二次函数的解析式为:y=x2﹣6;
(2)设二次函数的解析式为:y=a(x+3)2+k,
由题意得:,
解得:,
∴y=﹣(x+3)2﹣,
∴m=﹣(m+3)2﹣,
解得:m=﹣5或m=﹣6;
(3)当抛物线的顶点为:(0,﹣6),且过(﹣1,﹣5)时,有y=x2﹣6,
当x=y时有x=x2﹣6,
解得:x=﹣2或x=3,
∴m≤﹣2或m≥3.
20.(8分)水果店新进一种水果,进价为每千克5元,每天的销售量y(kg)与销售单价x(元)之间满足一次函数关系式,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)水果的销售单价定为多少元时,水果店卖这种水果每天获得的利润最大?最大利润是多少元?
【分析】(1)根据图示,运用待定系数法即可求解;
(2)根据销售利润的计算方法,结合二次函数图象的性质即可求解.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可知:,
解得:,
∴y与x的函数关系式为y=﹣20x+220.
(2)设每天销售这种水果所获的利润为w元,
∵y=﹣20x+220,
∴w=(x﹣5)×y=(x﹣5)(﹣20x+220)=﹣20x2+320x﹣1100=﹣20(x﹣8)2+180,
∴当x=8时,w有最大值,最大值为180,
∴售价定为8元/件时,每天最大利润为180元.
21.(12分)如图,顶点M在y轴负半轴上的抛物线与直线y=x+2相交于点A(﹣2,0),B(4,6),连接AM,BM.
(1)求该抛物线的函数表达式;
(2)若将抛物线向下平移3个单位长度,则在平移后的抛物线上,且在直线AB的下方,是否存在点P,使得S△ABP=S△ABM?若存在,求出点P的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法求解求得;
(2)先计算△ABM的面积,根据S△ABP=S△ABM,可得△ABP的面积,在y轴上取一点D,使S△ABD=S△ABM,过点D作AB的平行线交平移后的抛物线于点P,求得D点的坐标,即可求得直线PD的解析式,与平移后的抛物线解析式联立,解方程组即可求得P点坐标.
【解答】解:(1)设抛物线解析式为y=ax2+b,
∵抛物线经过点A(﹣2,0),B(4,6),
∴,
解得,
∴该抛物线的函数表达式为y=;
(3)令x=0,则y=x+2=2,
∴C(0,2),
∵M(0,﹣2),
∴CM=4,
∴S△ABM==12,
∵S△ABP=S△ABM,
∴S△ABP=×12=,
在y轴上取一点D,使S△ABD=S△ABM,过点D作AB的平行线交平移后的抛物线于点P,
∴CD (4+2)=,
∴CD=,
∵C(0,2),
∴OD==,
∴D(0,﹣),
∴直线PD的解析式为为y=﹣,
将抛物线向下平移3个单位长度,得到y=,
令﹣=,整理得x2﹣x﹣3=0,
解得x=,
y==,
∴P点的坐标为(,)或(,).
22.(12分)如图是一个东西走向近似于抛物线的山坡,以地面的东西方向为x轴、西侧的坡底为原点建立平面直角坐标系,山坡近似满足函数表达式y=﹣x,无人机从西侧距坡底O为10米处的B点起飞,沿山坡由西向东飞行,飞行轨迹近似满足抛物线y=﹣x2+bx+c,当无人机飞越坡底上空时(即点D,与地面的距离为20米.
(1)求无人机飞行轨迹的函数表达式,并写出自变量x的取值范围;
(2)当无人机飞行的水平距离距起点为30米时,求无人机与山坡的竖直距离d;
(3)由于山坡上有障碍物,无人机不能离山坡过近.当无人机与山坡的竖直距离大于9米时,无人机飞行才是安全的,请判断无人机此次飞行是否安全,并说明理由.
【分析】(1)把点 B(﹣10,0),D(0,20)代入,解答即可;
(2)根据已知求得无人机与山坡的竖直距离d=,把x=20代入求得即可;
(3)无人机与山坡的竖直距离d=,d的最小值与9比较即可得解.
【解答】解:(1)由题意可知,点 B(﹣10,0),D(0,20),将B,D坐标分别代入y=+bx+c,
得:,
解得:,
∴无人机飞行轨迹的函数表达式 为;
令y=0,则
解得:x1=﹣10,x2=100,
∴x的取值范围为﹣10≤x≤100;
(2)当无人机飞行的水平距离距起点为30米 时,x=30﹣10=20,
∵无人机与山坡的竖直距离d=+x+=,
∴当x=20时,d=﹣+20=13(米),
答:当无人机飞行的水平距离距起点为30米时,无人机与山坡的竖直距离d为13米;
(3)安全,理由如下:
由(2)知,d====,
∵,
∴x=45时,d有最小值,
∴无人机此次飞行是安全的.
23.(14分)如图,抛物线y=ax2+4x+c与直线y=﹣x+5交x轴于点A,交y轴于点B.
(1)求抛物线的解析式,并求出当﹣2≤x≤3时,y的取值范围;
(2)抛物线与x轴另一交点为E,连接BE,在抛物线上是否存在点F,使得∠ABF=∠ABE,若存在请求出点F的坐标,若不存在说明理由.
(3)如图2,以AB为边作矩形ABCD,设点C的横坐标为m.当CD边与抛物线只有一个公共点时,请直接写出m的取值范围.
【分析】(1)根据直线y=﹣x+5交x轴于点A,交y轴于点B,求出点A,点B的坐标,根据点A,点B在抛物线上,可求出抛物线的解析式,再根据﹣2≤x≤3,求出y的取值范围;
(2)由(1)得,抛物线为y=﹣x2+4x+5,求出点E,将△ABE沿直线AB折叠得到△ABE′,AE′与抛物线的交点为点F,则∠ABF=∠ABE,根据折叠的性质,交点坐标,即可求出点F的坐标;
(3)如图所示,延长DA交抛物线于点D2交y轴于点Q,过点D2作C2D2⊥AD交AD延长线于C2,CC2交x轴于P,根据矩形的性质,全等三角形的判定和性质,求出点P,Q的坐标,求出直线CC2的解析式和直线DD2的解析式,根据线段CD沿直线CC2移动,在C1C2之间时,CD与抛物线只有一个交点,求出m,即可.
【解答】解:(1)∵直线y=﹣x+5交x轴于点A,交y轴于点B,
∴A(5,0),B(0,5);
∵点A,点B在抛物线y=ax2+4x+c上,
∴,
解得:,
∴抛物线y=﹣x2+4x+5,
∴抛物线y=﹣x2+4x+5的对称轴为:x=2,
∴y=﹣(x﹣2)2+9,
当﹣2≤x≤2时,﹣7≤y≤9,
当2≤x≤3时,8≤y≤9,
∴当﹣2≤x≤3时,﹣7≤y≤9;
(2)存在,理由如下:
∵抛物线y=﹣x2+4x+5与x轴另一交点为E,
∴点E(﹣1,0),
将△ABE沿直线AB折叠得到△ABE′,AE′与抛物线的交点为点F,
∴∠ABF=∠ABE,
∴EE′的中点G(2,3),
∴点E′(5,6),
设直线BE′的解析式为:y=kx+b(k≠0),
∴,
解得:,
∴,
设点F(a,﹣a2+4a+5),
∵点F在直线上,
∴,
解得:a1=0(舍去),,
∴,
∴点;
(3)如图所示,延长DA交抛物线于点D2交y轴于点Q,过点D2作C2D2⊥AD交AD延长线于C2,CC2交x轴于P,
∵直线AB的解析式为y=﹣x+5,
∵四边形ABCD是矩形,
∴CC2⊥AB,DD2⊥AB,
∵A(5,0),B(0,5),
∴△ABO是等腰直角三角形,
∴∠PBO=45°,∠QAO=45°
∴△POB≌△BOA(AAS),△BOA≌△QOA(AAS),
∴OP=OA=5,QO=BO=5,
∴P(﹣5,0),Q(0,﹣5),
∴设直线CC2的解析式为y=k1x+b1(k≠0),直线DD2的解析式为:y=k2x+b2,
∴,,
解得:,,
∴直线CC2的解析式为y=x+5,直线DD2的解析式为y=x﹣5,
当线段CD沿直线CC2移动,在C1C2之间时,CD与抛物线只有一个交点,
∴,
∴C1(3,8);
∴,
∴D2(﹣2,﹣7),
∵四边形ABC2D2是矩形,
∴AB=C2D2,
∵直线AB向下平移7个单位,向左平移2个单位,得到C2D2,
∴C2(﹣7,﹣2),
∵C在C1C2间(包含端点,不与B重合)时,CD与抛物线只有一个交点,
∴﹣7≤m≤3且m≠0.
第1章 二次函数 单元经典题型检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B. C.y=(x+2)(x+1)﹣x2 D.y=2x2+3x
2.抛物线y=3(x﹣2)2+1的顶点坐标是( )
A.(2,1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
3.抛物线y=﹣3(x﹣4)2﹣5的最大值为( )
A.4 B.﹣4 C.5 D.﹣5
4.已知抛物线y=x2+mx的对称轴为直线x=2,则m的值是( )
A.4 B.2 C.﹣2 D.﹣4
5.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
6.已知抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,则方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为( )
A.x1=x2=2 B.x1=﹣1,x2=3 C.x1=0,x2=4 D.x1=﹣2,x2=2
7.如图,李大爷用24米长的篱笆靠墙围成一个长方形(ABCD)菜园,若菜园靠墙的一边(AD)长为x(米),那么菜园的面积y(平方米)与x的关系式为( )
A. B.y=x(12﹣x) C. D.y=x(24﹣x)
8.在平面直角坐标系中,将二次函数y=(x+1)2的图象关于x轴对称后,再向下平移2个单位长度所得抛物线对应的函数表达式为( )
A.y=(x+1)2﹣2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x+1)2+2
9.若函数y=x2﹣2x﹣m与x轴没有交点,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限.
A.一 B.二 C.三 D.四
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2﹣4ac>0,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分24分,每小题4分)
11.如果函数+3是二次函数,则m的值为 .
12.若抛物线y=﹣x2+4x﹣n的顶点在x轴的下方,则实数n的取值范围是 .
13.已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … ﹣5 0 3 4 3 m ﹣5 …
根据表格内容,该二次函数的m值为 .
14.已知点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,如果MN∥x轴,那么点N的坐标为 .
15.某种型号的小型无人机着陆后滑行的距离S(米)关于滑行的时间t(秒)的函数解析式是S=﹣0.25t2+8t,无人机着陆后滑行 秒才能停下来.
16.已知直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,则b取值范围是 .
三.解答题(共7小题,满分66分)
17.(6分)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=﹣2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
18.(6分)在如图所示的平面直角坐标系中,画出y=x2﹣4x+3的图象.
19.(8分)已知二次函数的图象经过A(0,﹣6)、B(﹣1,﹣5)、C(m,m)三点.
(1)若点A为该函数图象的顶点,求二次函数的表达式;
(2)若该函数图象的对称轴为直线x=﹣3,求m的值;
(3)若a>0,当﹣1<x<0时,y随x的增大而减小.结合图象,直接写出m的取值范围.
20.(8分)水果店新进一种水果,进价为每千克5元,每天的销售量y(kg)与销售单价x(元)之间满足一次函数关系式,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)水果的销售单价定为多少元时,水果店卖这种水果每天获得的利润最大?最大利润是多少元?
21.(12分)如图,顶点M在y轴负半轴上的抛物线与直线y=x+2相交于点A(﹣2,0),B(4,6),连接AM,BM.
(1)求该抛物线的函数表达式;
(2)若将抛物线向下平移3个单位长度,则在平移后的抛物线上,且在直线AB的下方,是否存在点P,使得S△ABP=S△ABM?若存在,求出点P的坐标;若不存在,请说明理由.
22.(12分)如图是一个东西走向近似于抛物线的山坡,以地面的东西方向为x轴、西侧的坡底为原点建立平面直角坐标系,山坡近似满足函数表达式y=﹣x,无人机从西侧距坡底O为10米处的B点起飞,沿山坡由西向东飞行,飞行轨迹近似满足抛物线y=﹣x2+bx+c,当无人机飞越坡底上空时(即点D,与地面的距离为20米.
(1)求无人机飞行轨迹的函数表达式,并写出自变量x的取值范围;
(2)当无人机飞行的水平距离距起点为30米时,求无人机与山坡的竖直距离d;
(3)由于山坡上有障碍物,无人机不能离山坡过近.当无人机与山坡的竖直距离大于9米时,无人机飞行才是安全的,请判断无人机此次飞行是否安全,并说明理由.
23.(14分)如图,抛物线y=ax2+4x+c与直线y=﹣x+5交x轴于点A,交y轴于点B.
(1)求抛物线的解析式,并求出当﹣2≤x≤3时,y的取值范围;
(2)抛物线与x轴另一交点为E,连接BE,在抛物线上是否存在点F,使得∠ABF=∠ABE,若存在请求出点F的坐标,若不存在说明理由.
(3)如图2,以AB为边作矩形ABCD,设点C的横坐标为m.当CD边与抛物线只有一个公共点时,请直接写出m的取值范围.
第1章 二次函数 单元经典题型检测卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.下列y关于x的函数中,一定是二次函数的是( )
A.y=(a+2)x2+1 B.
C.y=(x+2)(x+1)﹣x2 D.y=2x2+3x
【分析】根据二次函数的一般形式:形如y=ax2+bx+c(a,b,c为常数且a≠0),逐一判断即可解答.
【解答】解:A、y=(a+2)x2+1(a≠﹣2),是二次函数,故A不符合题意;
B、y=+1,不是二次函数,故B不符合题意;
C、y=(x+2)(x+1)﹣x2=3x+2,是一次函数,故C不符合题意;
D、y=2x2+3x,是二次函数,故D符合题意;
故选:D.
2.抛物线y=3(x﹣2)2+1的顶点坐标是( )
A.(2,1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
【分析】直接由抛物线解析式可求得答案.
【解答】解:∵y=3(x﹣2)2+1,
∴抛物线顶点坐标为(2,1),
故选:A.
3.抛物线y=﹣3(x﹣4)2﹣5的最大值为( )
A.4 B.﹣4 C.5 D.﹣5
【分析】所给抛物线是顶点式,可直接得出抛物线的对称轴.
【解答】解:∵抛物线y=a(x+h)2+k的最大值是k,
∴抛物线y=﹣3(x﹣4)2﹣5的最大值为﹣5.
故选:D.
4.已知抛物线y=x2+mx的对称轴为直线x=2,则m的值是( )
A.4 B.2 C.﹣2 D.﹣4
【分析】根据二次函数对称轴的公式即可求解.
【解答】解:y=x2+mx,
∴对称轴为直线x==2,
解得m=﹣4,
故选:D.
5.在同一平面直角坐标系中,一次函数y=mx﹣n的图象和二次函数y=mx2+nx的图象可能是( )
A. B.
C. D.
【分析】利用对称轴x=﹣,左同右异判断对称轴位置,结合一次函数图象走向与二次函数开口方向逐个判断即可.
【解答】解:A,结合图象y=mx﹣n中,m>0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣<0,与图象不符,不符合题意;
B,结合图象y=mx﹣n中,m>0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣<0,图象没过原点,与图象不合,不符合题意;
C,结合图象y=mx﹣n中,m>0,n<0,此时二次函数y=mx2+nx中对称轴x=﹣>0,与图象不符,不符合题意;
D,结合图象y=mx﹣n中,m<0,n>0,此时二次函数y=mx2+nx中对称轴x=﹣>0与图象符合,符合题意;
故选:D.
6.已知抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,则方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为( )
A.x1=x2=2 B.x1=﹣1,x2=3 C.x1=0,x2=4 D.x1=﹣2,x2=2
【分析】先将方程(x﹣1)2+m2=2m(x﹣1)﹣n化简,再根据抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点和二次函数图象平移的特点,即可写出抛物线y=(x﹣m﹣1)2+n与x轴交于(0,0)、(4,0)两点,然后即可得到方程(x﹣1)2+m2=2m(x﹣1)﹣n的解.
【解答】解:(x﹣1)2+m2=2m(x﹣1)﹣n,
化简,得:(x﹣m﹣1)2+n=0,
∵抛物线y=(x﹣m)2+n与x轴交于(﹣1,0)、(3,0)两点,
∴抛物线y=(x﹣m﹣1)2+n与x轴交于(0,0)、(4,0)两点,
∴方程(x﹣1)2+m2=2m(x﹣1)﹣n的解为x1=0,x2=4,
故选:C.
7.如图,李大爷用24米长的篱笆靠墙围成一个长方形(ABCD)菜园,若菜园靠墙的一边(AD)长为x(米),那么菜园的面积y(平方米)与x的关系式为( )
A. B.y=x(12﹣x) C. D.y=x(24﹣x)
【分析】根据AD的边长为x米,可以得出AB的长为米,然后根据矩形的面积公式即可求出函数关系式.
【解答】解:∵AD的边长为x米,而菜园ABCD是矩形菜园,
∴AB=米,
∵菜园的面积=AD×AB=x ,
∴y=.
故选:C.
8.在平面直角坐标系中,将二次函数y=(x+1)2的图象关于x轴对称后,再向下平移2个单位长度所得抛物线对应的函数表达式为( )
A.y=(x+1)2﹣2 B.y=﹣(x﹣1)2+2
C.y=﹣(x+1)2﹣2 D.y=﹣(x+1)2+2
【分析】直接利用关于x对称的点横坐标不变,纵坐标互为相反数得到关于x轴对称后的解析式,进而利用上下平移规律得出答案.
【解答】解:将二次函数y=(x+1)2的图象关于x轴对称后,得抛物线解析式为:﹣y=(x+1)2,即y=﹣(x+1)2,再向下平移2个单位长度所得抛物线对应的函数表达式是:y=﹣(x+1)2﹣2.
故选:C.
9.若函数y=x2﹣2x﹣m与x轴没有交点,则一次函数y=(m+1)x+m﹣1的图象不经过第( )象限.
A.一 B.二 C.三 D.四
【分析】由二次函数y=x2﹣2x﹣m与x轴没有交点,可知Δ<0,得出m<﹣1,然后根据m的取值判定m+1,m﹣1的取值即可.
【解答】解:∵二次函数y=x2﹣2x﹣m与x轴没有交点,
∴Δ<0,即4+4m<0,
∴m<﹣1,
∴m+1<0,m﹣1<0,
一次函数经过二、三、四象限,不经过第一象限.
故选:A.
10.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④b2﹣4ac>0,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线开口方向得到a<0以及函数经过原点即可判断①,根据x=1时的函数值可以判断②;由抛物线的对称轴方程得到为b=2a<0,以及a的符号即可判断③;根据抛物线与x轴交点个数得到Δ=b2﹣4ac>0,则可对④进行判断.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线经过原点,
∴c=0,
则abc=0,所以①正确;
当x=1时,函数值是a+b+c<0,则②错误;
∵抛物线的对称轴为直线x=﹣=﹣<0,
∴b=3a<0,
又∵a<0,
∴a>b,则③正确;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以④正确.
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
11.如果函数+3是二次函数,则m的值为 2 .
【分析】由二次函数的定义进行计算,即可得到答案.
【解答】解:∵是二次函数,
∴,
解得:,
∴m=2;
故答案为:2.
12.若抛物线y=﹣x2+4x﹣n的顶点在x轴的下方,则实数n的取值范围是 n>4 .
【分析】先根据函数解析式得出抛物线的开口向下,根据顶点在x轴的下方得出Δ<0,求出即可.
【解答】解:∵抛物线y=﹣x2+4x﹣n的开口向下,顶点在x轴的下方,
而与x轴没有交点,
方程﹣x2+4x﹣n=0无实数根,
即b2﹣4ac=16﹣4n<0,
∴n>4.
故答案为:n>4.
13.已知二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … ﹣5 0 3 4 3 m ﹣5 …
根据表格内容,该二次函数的m值为 0 .
【分析】由表格个可得抛物线对称轴,再由抛物线对称性求解.
【解答】解:由表格可得抛物线经过(﹣2,3),(0,3),
∴抛物线对称轴为直线x=﹣1,
∴(﹣3,0),(1,m)关于对称轴对称,
∴m=0,
故答案为:0.
14.已知点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,如果MN∥x轴,那么点N的坐标为 (3,2) .
【分析】根据抛物线的对称性即可求得点N的坐标.
【解答】解:∵抛物线y=x2﹣2x+c,
∴抛物线的对称轴为直线x=﹣=1,
∵点M(﹣1,2)和点N都在抛物线y=x2﹣2x+c上,且MN∥x轴,
∴M、N关于直线x=1对称,
∴点N的坐标为(3,2).
故答案为:(3,2).
15.某种型号的小型无人机着陆后滑行的距离S(米)关于滑行的时间t(秒)的函数解析式是S=﹣0.25t2+8t,无人机着陆后滑行 16 秒才能停下来.
【分析】飞机停下时,也就是滑行距离最远时,即在本题中需求出s最大时对应的t值.
【解答】解:由题意得,
S=﹣0.25t2+8t
=﹣0.25(t2﹣32t+256﹣256)
=﹣0.25(t﹣16)2+64,
∵﹣0.25<0,
∴t=16时,飞机滑行的距离最大,
即当t=16秒时,飞机才能停下来.
故答案为:16.
16.已知直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,则b取值范围是 ﹣1<b≤3 .
【分析】画出y=x2﹣4|x|+3图象即可求解.
【解答】解:根据描点法画出y=x2﹣4|x|+3图象,如图所示,
若直线y=b与函数y=x2﹣4|x|+3的图象至少3个交点,
由图象可得:﹣1<b≤3,
故答案为:﹣1<b≤3.
三.解答题(共7小题,满分66分)
17.(6分)已知二次函数y=ax2,当x=3时,y=3.
(1)求当x=﹣2时,y的值.
(2)写出它的图象的对称轴、顶点坐标和开口方向.
【分析】(1)把x=3,y=3代入y=ax2求出a,得到这个二次函数的表达式,再将x=﹣2代入即可求出y的值;
(2)根据a的符号判断抛物线的开口方向,把抛物线解析式化为顶点式,进而求出对称轴、顶点坐标.
【解答】解:(1)把x=3,y=3代入y=ax2得,
a 32=3,解得a=,
所以这个二次函数的表达式为y=x2;
当x=﹣2时,y=×(﹣2)2=;
(2)∵y=x2,a=>0,
∴图象开口向上;
对称轴是直线x=0,顶点坐标是(0,0).
18.(6分)在如图所示的平面直角坐标系中,画出y=x2﹣4x+3的图象.
【分析】根据函数解析式,求出对称轴、交点坐标与y轴交点坐标,用平滑的曲线连接即可.
【解答】解:由题意可知,
y=x2﹣4x+3与x轴的交点坐标为(1,0)和(3,0),与y轴的交点为(0,3),
对称轴为x===2,
顶点坐标为(2,﹣1),
如图,
.
19.(8分)已知二次函数的图象经过A(0,﹣6)、B(﹣1,﹣5)、C(m,m)三点.
(1)若点A为该函数图象的顶点,求二次函数的表达式;
(2)若该函数图象的对称轴为直线x=﹣3,求m的值;
(3)若a>0,当﹣1<x<0时,y随x的增大而减小.结合图象,直接写出m的取值范围.
【分析】(1)先设抛物线的顶点式,再代入求解;
(2)先设抛物线的顶点式,再求出解析式,再求出当x=y时的x值;
(3)由题意得:抛物线的对称轴为:x≥0,结合图象求解.
【解答】解:(1)设二次函数的解析式为:y=ax2﹣6,
由题意得:a﹣6=﹣5,
解得:a=1,
∴二次函数的解析式为:y=x2﹣6;
(2)设二次函数的解析式为:y=a(x+3)2+k,
由题意得:,
解得:,
∴y=﹣(x+3)2﹣,
∴m=﹣(m+3)2﹣,
解得:m=﹣5或m=﹣6;
(3)当抛物线的顶点为:(0,﹣6),且过(﹣1,﹣5)时,有y=x2﹣6,
当x=y时有x=x2﹣6,
解得:x=﹣2或x=3,
∴m≤﹣2或m≥3.
20.(8分)水果店新进一种水果,进价为每千克5元,每天的销售量y(kg)与销售单价x(元)之间满足一次函数关系式,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)水果的销售单价定为多少元时,水果店卖这种水果每天获得的利润最大?最大利润是多少元?
【分析】(1)根据图示,运用待定系数法即可求解;
(2)根据销售利润的计算方法,结合二次函数图象的性质即可求解.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可知:,
解得:,
∴y与x的函数关系式为y=﹣20x+220.
(2)设每天销售这种水果所获的利润为w元,
∵y=﹣20x+220,
∴w=(x﹣5)×y=(x﹣5)(﹣20x+220)=﹣20x2+320x﹣1100=﹣20(x﹣8)2+180,
∴当x=8时,w有最大值,最大值为180,
∴售价定为8元/件时,每天最大利润为180元.
21.(12分)如图,顶点M在y轴负半轴上的抛物线与直线y=x+2相交于点A(﹣2,0),B(4,6),连接AM,BM.
(1)求该抛物线的函数表达式;
(2)若将抛物线向下平移3个单位长度,则在平移后的抛物线上,且在直线AB的下方,是否存在点P,使得S△ABP=S△ABM?若存在,求出点P的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法求解求得;
(2)先计算△ABM的面积,根据S△ABP=S△ABM,可得△ABP的面积,在y轴上取一点D,使S△ABD=S△ABM,过点D作AB的平行线交平移后的抛物线于点P,求得D点的坐标,即可求得直线PD的解析式,与平移后的抛物线解析式联立,解方程组即可求得P点坐标.
【解答】解:(1)设抛物线解析式为y=ax2+b,
∵抛物线经过点A(﹣2,0),B(4,6),
∴,
解得,
∴该抛物线的函数表达式为y=;
(3)令x=0,则y=x+2=2,
∴C(0,2),
∵M(0,﹣2),
∴CM=4,
∴S△ABM==12,
∵S△ABP=S△ABM,
∴S△ABP=×12=,
在y轴上取一点D,使S△ABD=S△ABM,过点D作AB的平行线交平移后的抛物线于点P,
∴CD (4+2)=,
∴CD=,
∵C(0,2),
∴OD==,
∴D(0,﹣),
∴直线PD的解析式为为y=﹣,
将抛物线向下平移3个单位长度,得到y=,
令﹣=,整理得x2﹣x﹣3=0,
解得x=,
y==,
∴P点的坐标为(,)或(,).
22.(12分)如图是一个东西走向近似于抛物线的山坡,以地面的东西方向为x轴、西侧的坡底为原点建立平面直角坐标系,山坡近似满足函数表达式y=﹣x,无人机从西侧距坡底O为10米处的B点起飞,沿山坡由西向东飞行,飞行轨迹近似满足抛物线y=﹣x2+bx+c,当无人机飞越坡底上空时(即点D,与地面的距离为20米.
(1)求无人机飞行轨迹的函数表达式,并写出自变量x的取值范围;
(2)当无人机飞行的水平距离距起点为30米时,求无人机与山坡的竖直距离d;
(3)由于山坡上有障碍物,无人机不能离山坡过近.当无人机与山坡的竖直距离大于9米时,无人机飞行才是安全的,请判断无人机此次飞行是否安全,并说明理由.
【分析】(1)把点 B(﹣10,0),D(0,20)代入,解答即可;
(2)根据已知求得无人机与山坡的竖直距离d=,把x=20代入求得即可;
(3)无人机与山坡的竖直距离d=,d的最小值与9比较即可得解.
【解答】解:(1)由题意可知,点 B(﹣10,0),D(0,20),将B,D坐标分别代入y=+bx+c,
得:,
解得:,
∴无人机飞行轨迹的函数表达式 为;
令y=0,则
解得:x1=﹣10,x2=100,
∴x的取值范围为﹣10≤x≤100;
(2)当无人机飞行的水平距离距起点为30米 时,x=30﹣10=20,
∵无人机与山坡的竖直距离d=+x+=,
∴当x=20时,d=﹣+20=13(米),
答:当无人机飞行的水平距离距起点为30米时,无人机与山坡的竖直距离d为13米;
(3)安全,理由如下:
由(2)知,d====,
∵,
∴x=45时,d有最小值,
∴无人机此次飞行是安全的.
23.(14分)如图,抛物线y=ax2+4x+c与直线y=﹣x+5交x轴于点A,交y轴于点B.
(1)求抛物线的解析式,并求出当﹣2≤x≤3时,y的取值范围;
(2)抛物线与x轴另一交点为E,连接BE,在抛物线上是否存在点F,使得∠ABF=∠ABE,若存在请求出点F的坐标,若不存在说明理由.
(3)如图2,以AB为边作矩形ABCD,设点C的横坐标为m.当CD边与抛物线只有一个公共点时,请直接写出m的取值范围.
【分析】(1)根据直线y=﹣x+5交x轴于点A,交y轴于点B,求出点A,点B的坐标,根据点A,点B在抛物线上,可求出抛物线的解析式,再根据﹣2≤x≤3,求出y的取值范围;
(2)由(1)得,抛物线为y=﹣x2+4x+5,求出点E,将△ABE沿直线AB折叠得到△ABE′,AE′与抛物线的交点为点F,则∠ABF=∠ABE,根据折叠的性质,交点坐标,即可求出点F的坐标;
(3)如图所示,延长DA交抛物线于点D2交y轴于点Q,过点D2作C2D2⊥AD交AD延长线于C2,CC2交x轴于P,根据矩形的性质,全等三角形的判定和性质,求出点P,Q的坐标,求出直线CC2的解析式和直线DD2的解析式,根据线段CD沿直线CC2移动,在C1C2之间时,CD与抛物线只有一个交点,求出m,即可.
【解答】解:(1)∵直线y=﹣x+5交x轴于点A,交y轴于点B,
∴A(5,0),B(0,5);
∵点A,点B在抛物线y=ax2+4x+c上,
∴,
解得:,
∴抛物线y=﹣x2+4x+5,
∴抛物线y=﹣x2+4x+5的对称轴为:x=2,
∴y=﹣(x﹣2)2+9,
当﹣2≤x≤2时,﹣7≤y≤9,
当2≤x≤3时,8≤y≤9,
∴当﹣2≤x≤3时,﹣7≤y≤9;
(2)存在,理由如下:
∵抛物线y=﹣x2+4x+5与x轴另一交点为E,
∴点E(﹣1,0),
将△ABE沿直线AB折叠得到△ABE′,AE′与抛物线的交点为点F,
∴∠ABF=∠ABE,
∴EE′的中点G(2,3),
∴点E′(5,6),
设直线BE′的解析式为:y=kx+b(k≠0),
∴,
解得:,
∴,
设点F(a,﹣a2+4a+5),
∵点F在直线上,
∴,
解得:a1=0(舍去),,
∴,
∴点;
(3)如图所示,延长DA交抛物线于点D2交y轴于点Q,过点D2作C2D2⊥AD交AD延长线于C2,CC2交x轴于P,
∵直线AB的解析式为y=﹣x+5,
∵四边形ABCD是矩形,
∴CC2⊥AB,DD2⊥AB,
∵A(5,0),B(0,5),
∴△ABO是等腰直角三角形,
∴∠PBO=45°,∠QAO=45°
∴△POB≌△BOA(AAS),△BOA≌△QOA(AAS),
∴OP=OA=5,QO=BO=5,
∴P(﹣5,0),Q(0,﹣5),
∴设直线CC2的解析式为y=k1x+b1(k≠0),直线DD2的解析式为:y=k2x+b2,
∴,,
解得:,,
∴直线CC2的解析式为y=x+5,直线DD2的解析式为y=x﹣5,
当线段CD沿直线CC2移动,在C1C2之间时,CD与抛物线只有一个交点,
∴,
∴C1(3,8);
∴,
∴D2(﹣2,﹣7),
∵四边形ABC2D2是矩形,
∴AB=C2D2,
∵直线AB向下平移7个单位,向左平移2个单位,得到C2D2,
∴C2(﹣7,﹣2),
∵C在C1C2间(包含端点,不与B重合)时,CD与抛物线只有一个交点,
∴﹣7≤m≤3且m≠0.
同课章节目录
