2022-2023学年浙教版数学八年级下册 第一章 二次根式:1.1二次根式课件 33张PPT
文档属性
| 名称 | 2022-2023学年浙教版数学八年级下册 第一章 二次根式:1.1二次根式课件 33张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
1.1 二次根式
浙教版八年级下册
学习目标
1、经历二次根式概念的发生过程,了解二次根式的概念.
2、理解二次根式何时有意义,何时无意义,会在简单情况下求根号内所有含字母的取值范围.
3、会求含字母的二次根式的值.
(1) 3的平方根是______
(2) 3的算术平方根是______
(3) 有意义吗?为什么?
(4)一个非负数a的算术平方根应表示为__________ .
想一想:
无意义.负数没有算数平方根.有意义.
新知导入
(1)如图,是一块长方形绿地,如果绿地长AB=4m,
宽BC=2m,那么中间连接相对两角的小路AC的长为多少m?
由勾股定理:
40m
A
am
B
C
2m
?
如果绿地长AB为am,宽BC为2m,又怎样求AC的长呢?
新知导入
(2)一块面积为b-3的正方形草坪,它每条边的长为多少?
(3)一块面积为scm2的等腰直角三角形的草坪,它的腰长为多少呢?
(b – 3)cm
思考:这3个代数式在形式上有什么共同特点吗?
①都表示算术平方根;
②根号里面的式子都含有字母.
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式.
注意:为了方便起见,我们把一个数的算术平方根也叫做二次根式.如
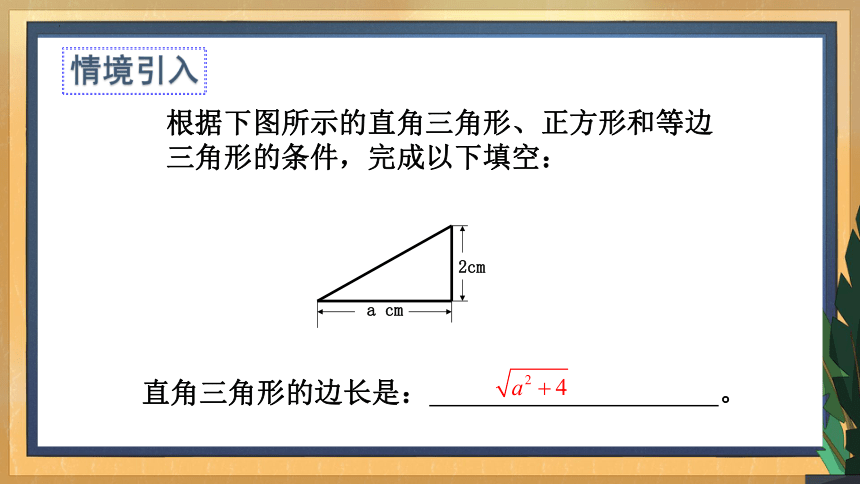
根据下图所示的直角三角形、正方形和等边三角形的条件,完成以下填空:
2cm
a cm
直角三角形的边长是: 。
情境引入
(b – 3)cm
正方形的边长是:
S
等腰直角三角形的的直角边长是
你认为所得的各代数式的共同特点是什么?
探究一
的共同特点:
表示的是算术平方根
根号内含有字母的代数式
归纳总结
为了方便起见,我们把一个数的算术平方根也叫二次根式。
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式。
例如: 也叫二次根式。
被开方数
二次根号
读作“根号 ”
下列代数式中哪些是二次根式?
⑴
⑵
⑶
⑷
⑸
⑹
练习 1
a取何值时,下列根式有意义
解:(1)∵a+1≥0,解得a≥-1。
解:(2)由
探究二
举一反三
(a为任何实数)
(a=1)
(a为任何实数)
变式
①被开方数≥0;
②分母中有字母时,分母≠0。
求二次根式中字母的取值范围的基本依据是什么呢?
归纳总结
求下列二次根式中字母的取值范围:
(1) (2)
(1)解:由题意得,
可取全体实数
(2)解:由题意得,
练习 2
(4)解:由题意得,
(3)解:由题意得,
(3) (4)
当x=-4时,求二次根式 的值。
解:将x=-4代入二次根式,得
探究三
1、若二次根式 的值增加3,求x的值
2、当x=-2时,求二次根式 的值
x=3或x=-3
x=1
练习 3
典题精讲
1.下列各式是二次根式吗
是
是
是
是
不是
不是
不是
不是
不是
不是
达标评测
2.x取何值时,下列二次根式有意义
(7)
解:由3-x≥0 得 x≤3
由|x|-4≠0 得 x≠±4
所以当
有意义
x ≤3且x≠-4时,
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零。
③多个条件组合时,应用不等式组求解
3. 已知
,求
的值.
解:由题意得,
4.若a.b为实数 ,且
求 的值。
解:
一艘轮船先向东北方向航行2小时,再向西
北方向航行t小时。船的航速是每时25千米。
1)、用关于t的代数式表示船离开出发地的距离。
2)、求当t=3时,船离开出发地多少千米。
(精确到0.01)
应用提高
东
北
解:(1)设船离出发地的距离为s千米
(2)当t=3时,
s=
1.二次根式的概念
课堂总结
2.二次根式有意义的条件
条件:二次根式根号内字母的取值范围必须满足被开方数____________________.
方法:根据二次根式的定义列不等式(或不等式组)求解.
拓展:求字母的取值范围是指求字母满足题目要求的条件,一般可分为两种类型思考:一类是求字母所在的式子有意义时字母满足的条件;另一类是求使字母所在的实际问题有意义时字母必须满足的条件.
大于或等于零
作业布置
教材5页习题第2、4题。
下 课 休 息
浙教版八年级下册
1.1 二次根式
浙教版八年级下册
学习目标
1、经历二次根式概念的发生过程,了解二次根式的概念.
2、理解二次根式何时有意义,何时无意义,会在简单情况下求根号内所有含字母的取值范围.
3、会求含字母的二次根式的值.
(1) 3的平方根是______
(2) 3的算术平方根是______
(3) 有意义吗?为什么?
(4)一个非负数a的算术平方根应表示为__________ .
想一想:
无意义.负数没有算数平方根.有意义.
新知导入
(1)如图,是一块长方形绿地,如果绿地长AB=4m,
宽BC=2m,那么中间连接相对两角的小路AC的长为多少m?
由勾股定理:
40m
A
am
B
C
2m
?
如果绿地长AB为am,宽BC为2m,又怎样求AC的长呢?
新知导入
(2)一块面积为b-3的正方形草坪,它每条边的长为多少?
(3)一块面积为scm2的等腰直角三角形的草坪,它的腰长为多少呢?
(b – 3)cm
思考:这3个代数式在形式上有什么共同特点吗?
①都表示算术平方根;
②根号里面的式子都含有字母.
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式.
注意:为了方便起见,我们把一个数的算术平方根也叫做二次根式.如
根据下图所示的直角三角形、正方形和等边三角形的条件,完成以下填空:
2cm
a cm
直角三角形的边长是: 。
情境引入
(b – 3)cm
正方形的边长是:
S
等腰直角三角形的的直角边长是
你认为所得的各代数式的共同特点是什么?
探究一
的共同特点:
表示的是算术平方根
根号内含有字母的代数式
归纳总结
为了方便起见,我们把一个数的算术平方根也叫二次根式。
像 这样表示的是算术平方根,且根号内含有字母的代数式叫二次根式。
例如: 也叫二次根式。
被开方数
二次根号
读作“根号 ”
下列代数式中哪些是二次根式?
⑴
⑵
⑶
⑷
⑸
⑹
练习 1
a取何值时,下列根式有意义
解:(1)∵a+1≥0,解得a≥-1。
解:(2)由
探究二
举一反三
(a为任何实数)
(a=1)
(a为任何实数)
变式
①被开方数≥0;
②分母中有字母时,分母≠0。
求二次根式中字母的取值范围的基本依据是什么呢?
归纳总结
求下列二次根式中字母的取值范围:
(1) (2)
(1)解:由题意得,
可取全体实数
(2)解:由题意得,
练习 2
(4)解:由题意得,
(3)解:由题意得,
(3) (4)
当x=-4时,求二次根式 的值。
解:将x=-4代入二次根式,得
探究三
1、若二次根式 的值增加3,求x的值
2、当x=-2时,求二次根式 的值
x=3或x=-3
x=1
练习 3
典题精讲
1.下列各式是二次根式吗
是
是
是
是
不是
不是
不是
不是
不是
不是
达标评测
2.x取何值时,下列二次根式有意义
(7)
解:由3-x≥0 得 x≤3
由|x|-4≠0 得 x≠±4
所以当
有意义
x ≤3且x≠-4时,
求二次根式中字母的取值范围的基本依据:
①被开方数大于等于零;
②分母中有字母时,要保证分母不为零。
③多个条件组合时,应用不等式组求解
3. 已知
,求
的值.
解:由题意得,
4.若a.b为实数 ,且
求 的值。
解:
一艘轮船先向东北方向航行2小时,再向西
北方向航行t小时。船的航速是每时25千米。
1)、用关于t的代数式表示船离开出发地的距离。
2)、求当t=3时,船离开出发地多少千米。
(精确到0.01)
应用提高
东
北
解:(1)设船离出发地的距离为s千米
(2)当t=3时,
s=
1.二次根式的概念
课堂总结
2.二次根式有意义的条件
条件:二次根式根号内字母的取值范围必须满足被开方数____________________.
方法:根据二次根式的定义列不等式(或不等式组)求解.
拓展:求字母的取值范围是指求字母满足题目要求的条件,一般可分为两种类型思考:一类是求字母所在的式子有意义时字母满足的条件;另一类是求使字母所在的实际问题有意义时字母必须满足的条件.
大于或等于零
作业布置
教材5页习题第2、4题。
下 课 休 息
浙教版八年级下册
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
