浙教版数学七年级上册单元训练卷(7) 实数(二)(考查知识点+答案详解+名师点评)
文档属性
| 名称 | 浙教版数学七年级上册单元训练卷(7) 实数(二)(考查知识点+答案详解+名师点评) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-09 00:00:00 | ||
图片预览




文档简介
浙教版数学七年级上册单元训练卷(7)
实数(二)
班级 姓名
一、选择题(每题3分,共30分)
1.计算:﹣2﹣5的结果是( )
A. ﹣7 B. ﹣3 C. 3 D. 7
2.首届中国(北京)国际服务贸易交易会(京交会),本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为( )
A. B. C. D.
3.在﹣3,﹣1,0,2这四个数中,最小的数是( ) A.﹣3 B.﹣1 C.0 D.221教育网
5. 如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( )
A.-7 ℃ B.+7 ℃ C.+12 ℃ D.-12 ℃
已知,则a+b=( )
A.﹣8 B.﹣6 C.6 D.8
7.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是( )
A.43 B.44 C.45 D.46
若与|x﹣y﹣3|互为相反数,则x+y的值为( )
A. 3 B. 9 C. 12 D. 27
9.如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )21·cn·jy·com
A.41 B.40 C.39 D.38
10.若,则m的值为( )
A.3 B.4 C.5 D. 6
二、填空题(每题4分,共24分)
1.计算:∣-2∣= ,= ,= ,=
。
2. 计算= .
3.若x,y为实数,且满足,则的值是 .
4、实数m、n在数轴上的位置如图所示,则|n﹣m|= .
5.计算= .
6.已知整数满足下列条件:,,,
,…,依次类推,则的值为 .
A. B. C. D.
三、解答题(17题6分,18题8分,23题12分,其余每题10分,共66分)
17.计算:.
18.(1) (2)
19.把代表下列各数的序号填在相应的大括号内。
② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0)
整数集合: { }
负分数集合:{ }
无理数集合:{ }
实数:{ }
20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;www.21-cn-jy.com
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
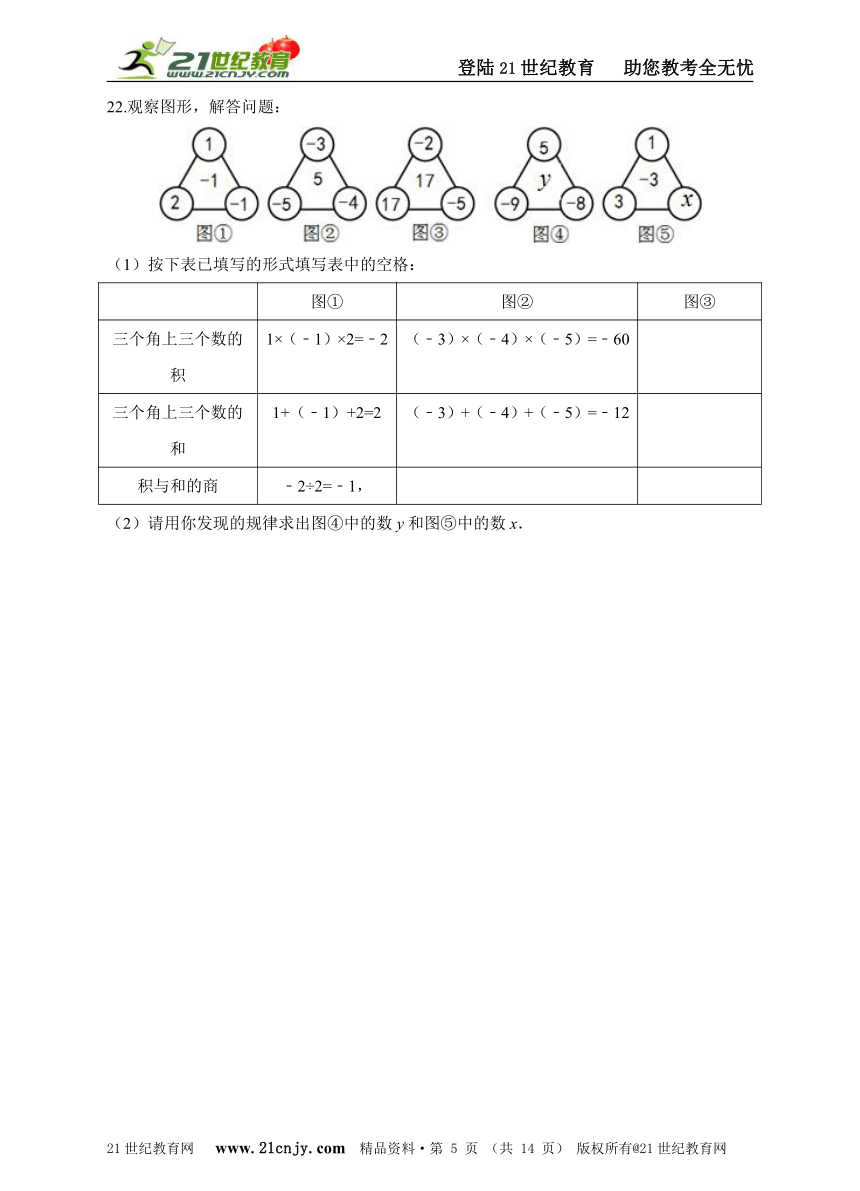
22.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
﹣2÷2=﹣1,
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
参考答案
一、选择题(每题3分,共30分)
1.计算:﹣2﹣5的结果是( )
A. ﹣7 B. ﹣3 C. 3 D. 7
【答案】A。
【考点】有理数的加法。
【分析】根据有理数的加法运算法则计算即可:﹣2﹣5=﹣(2+5)=﹣7。故选A。
2.首届中国(北京)国际服务贸易交易会(京交会),本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为( )
A. B. C. D.
【答案】C。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值。在确定n的值时,看该数是大于或等于1还是小于1。当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0)。60 110 000 000一共11位,从而60 110 000 000=6.011×1010。故选C。【来源:21·世纪·教育·网】
3.在﹣3,﹣1,0,2这四个数中,最小的数是( ) A.﹣3 B.﹣1 C.0 D.221·世纪*教育网
【答案】A。
【考点】有理数大小比较。
【分析】画数轴,这四个数在数轴上的位置如图所示:
由数轴的特点可知,这四个数中最小的数是﹣3。故选A。
5. 如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( )
A.-7 ℃ B.+7 ℃ C.+12 ℃ D.-12 ℃
【答案】A。
【考点】正数和负数。
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示。因此,
∵“正”和“负”相对,∴零上5℃记作+5℃,则零下7℃可记作-7℃。故选A。
6. 已知,则a+b=( ) A.﹣8 B.﹣6 C.6 D.8
【答案】B。
【考点】非负数的性质,绝对值,算术平方,求代数式的值。
【分析】∵,,∴a﹣1=0,7+b=0,解得a=1,b=﹣7。
∴a+b=1+(﹣7)=﹣6。故选B。
7.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是( )
A.43 B.44 C.45 D.46
【答案】C。
【考点】分类归纳(数字的变化类)。
【分析】分析规律,然后找出2013所在的奇数的范围,即可得解:
∵23=3+5,33=7+9+11,43=13+15+17+19,
…
∴m3分裂后的第一个数是m(m-1)+1,共有m个奇数。
∵45×(45-1)+1=1981,46×(46-1)+1=2071,
∴第2013个奇数是底数为45的数的立方分裂后的一个奇数,
∴m=45。故选C。
若与|x﹣y﹣3|互为相反数,则x+y的值为( )
A. 3 B. 9 C. 12 D. 27
【答案】D。
【考点】相反数,非负数的性质,算术平方根的性质,绝对值的性质。
【分析】∵与|x﹣y﹣3|互为相反数,∴+|x﹣y﹣3|=0,
∴,解得。∴x+y=12+15=27。故选D。
9.如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )2·1·c·n·j·y
A.41 B.40 C.39 D.38
【答案】C。
【考点】正方体相对两个面上的文字。
【分析】∵三个骰子18个面上的数字的总和为:3(1+2+3+4+5+6)=3×21=63,
看得见的7个面上的数字的和为:1+2+3+5+4+6+3=24,
∴看不见的面上的点数总和是:63﹣24=39。故选C。
10.若,则m的值为( )
A.3 B.4 C.5 D. 6
【答案】A。
【考点】幂的乘方,同底数幂的乘法。
【分析】∵,∴,即,即。
∴1+5m=11,解得m=2。故选A。
二、填空题(每题4分,共24分)
1.计算:∣-2∣= ▲ ,= ▲ ,= ▲ ,=
▲ 。
【答案】2,,4,3。
【考点】绝对值,负整数指数幂,有理数的乘方,立方根化简。
【分析】根据乘法分配律,同底幂乘法,合并同类项,幂的乘方运算法则逐一计算即可。
2. 计算= ▲ .
【答案】。
【考点】有理数的减法,绝对值。
【分析】。
3.若x,y为实数,且满足,则的值是 ▲ .
【答案】1。
【考点】非负数的性质,算术平方根,绝对值。
【分析】根据算术平方根和绝对值非负数的性质,要使,必须有且,即x=3,y=3。∴。
4、实数m、n在数轴上的位置如图所示,则|n﹣m|= ▲ .
【答案】m﹣n。
【考点】实数与数轴。
【分析】如图可得:n<m,即n﹣m<0,∴|n﹣m|=﹣(n﹣m)=m﹣n。
5.计算= ▲ .
【答案】。
【考点】实数的运算,算术平方根,负整数指数幂,零指数幂。
【分析】针对算术平方根,负整数指数幂,零指数幂3个考点分别进行计算,然后根据实数的运算法则求得计算结果:。
6.已知整数满足下列条件:,,,
,…,依次类推,则的值为 .
A. B. C. D.
【答案】B。
【考点】分类归纳(数字的变化类)
【分析】根据条件求出前几个数的值,寻找规律,分是奇数和偶数讨论::
∵, ,
,,
,,
,,
…,
∴当是奇数时,,是偶数时, 。
∴。故选B。
三、解答题(17题6分,18题8分,23题12分,其余每题10分,共66分)
17.计算:.
【答案】解:原式=2+1-5+1+9=8。
【考点】实数的运算,算术平方根,零指数幂,绝对值,乘方,负整数指数幂。
【分析】针对算术平方根,零指数幂,绝对值,乘方,负整数指数幂5个考点分别进行计算,然后根据实数的运算法则求得计算结果。21世纪教育网版权所有
18.(1) (2)
(1)
(2)
19.把代表下列各数的序号填在相应的大括号内。
② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0)
整数集合: { -5 0 }
负分数集合:{ - 0.86 - }
无理数集合:{ 1.1010010001...(每两个1之间依次多一个0)}
实数:{ ② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0) }
20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;21cnjy.com
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
解:(1)64,8,15;
(2),,;
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
【答案】解:(1)。
(2)。
(3)a1+a2+a3+a4+…+a100
。
【考点】分类归纳(数字的变化类)。
【分析】(1)(2)观察知,找等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1。
(3)运用变化规律计算。
22.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
﹣2÷2=﹣1,
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
【答案】解:(1)填表如下:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
(﹣2)×(﹣5)×17=170
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
(﹣2)+(﹣5)+17=17
积与和的商
﹣2÷2=﹣1
(﹣60)÷(﹣12)=5
170÷10=17
(2)图④:∵5×(﹣8)×(﹣9)=360,5+(﹣8)+(﹣9)=﹣1,
∴y=360÷(﹣12)=﹣30。
图⑤:由(1·x·3)÷(1+x+3)=﹣3,解得x=﹣2。.
【考点】分类归纳(数字的变化类)。
【分析】(1)根据图形和表中已填写的形式,即可求出表中的空格;
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,列出方程,即可求出x、y的值。
23.请你规定一种适合任意非零实数a,b的新运算“a⊕b”,使得下列算式成立:
1⊕2=2⊕1=3,(﹣3)⊕(﹣4)=(﹣4)⊕(﹣3)=﹣,(﹣3)⊕5=5⊕(﹣3)=﹣,…
你规定的新运算a⊕b=?(用a,b的一个代数式表示).
【答案】。
【考点】分类归纳(数字的变化类),新定义。
【分析】寻找规律:
∵,
,···
∴。
实数(二)
班级 姓名
一、选择题(每题3分,共30分)
1.计算:﹣2﹣5的结果是( )
A. ﹣7 B. ﹣3 C. 3 D. 7
2.首届中国(北京)国际服务贸易交易会(京交会),本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为( )
A. B. C. D.
3.在﹣3,﹣1,0,2这四个数中,最小的数是( ) A.﹣3 B.﹣1 C.0 D.221教育网
5. 如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( )
A.-7 ℃ B.+7 ℃ C.+12 ℃ D.-12 ℃
已知,则a+b=( )
A.﹣8 B.﹣6 C.6 D.8
7.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是( )
A.43 B.44 C.45 D.46
若与|x﹣y﹣3|互为相反数,则x+y的值为( )
A. 3 B. 9 C. 12 D. 27
9.如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )21·cn·jy·com
A.41 B.40 C.39 D.38
10.若,则m的值为( )
A.3 B.4 C.5 D. 6
二、填空题(每题4分,共24分)
1.计算:∣-2∣= ,= ,= ,=
。
2. 计算= .
3.若x,y为实数,且满足,则的值是 .
4、实数m、n在数轴上的位置如图所示,则|n﹣m|= .
5.计算= .
6.已知整数满足下列条件:,,,
,…,依次类推,则的值为 .
A. B. C. D.
三、解答题(17题6分,18题8分,23题12分,其余每题10分,共66分)
17.计算:.
18.(1) (2)
19.把代表下列各数的序号填在相应的大括号内。
② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0)
整数集合: { }
负分数集合:{ }
无理数集合:{ }
实数:{ }
20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;www.21-cn-jy.com
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
22.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
﹣2÷2=﹣1,
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
参考答案
一、选择题(每题3分,共30分)
1.计算:﹣2﹣5的结果是( )
A. ﹣7 B. ﹣3 C. 3 D. 7
【答案】A。
【考点】有理数的加法。
【分析】根据有理数的加法运算法则计算即可:﹣2﹣5=﹣(2+5)=﹣7。故选A。
2.首届中国(北京)国际服务贸易交易会(京交会),本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为( )
A. B. C. D.
【答案】C。
【考点】科学记数法。
【分析】根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值。在确定n的值时,看该数是大于或等于1还是小于1。当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0)。60 110 000 000一共11位,从而60 110 000 000=6.011×1010。故选C。【来源:21·世纪·教育·网】
3.在﹣3,﹣1,0,2这四个数中,最小的数是( ) A.﹣3 B.﹣1 C.0 D.221·世纪*教育网
【答案】A。
【考点】有理数大小比较。
【分析】画数轴,这四个数在数轴上的位置如图所示:
由数轴的特点可知,这四个数中最小的数是﹣3。故选A。
5. 如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( )
A.-7 ℃ B.+7 ℃ C.+12 ℃ D.-12 ℃
【答案】A。
【考点】正数和负数。
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示。因此,
∵“正”和“负”相对,∴零上5℃记作+5℃,则零下7℃可记作-7℃。故选A。
6. 已知,则a+b=( ) A.﹣8 B.﹣6 C.6 D.8
【答案】B。
【考点】非负数的性质,绝对值,算术平方,求代数式的值。
【分析】∵,,∴a﹣1=0,7+b=0,解得a=1,b=﹣7。
∴a+b=1+(﹣7)=﹣6。故选B。
7.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是( )
A.43 B.44 C.45 D.46
【答案】C。
【考点】分类归纳(数字的变化类)。
【分析】分析规律,然后找出2013所在的奇数的范围,即可得解:
∵23=3+5,33=7+9+11,43=13+15+17+19,
…
∴m3分裂后的第一个数是m(m-1)+1,共有m个奇数。
∵45×(45-1)+1=1981,46×(46-1)+1=2071,
∴第2013个奇数是底数为45的数的立方分裂后的一个奇数,
∴m=45。故选C。
若与|x﹣y﹣3|互为相反数,则x+y的值为( )
A. 3 B. 9 C. 12 D. 27
【答案】D。
【考点】相反数,非负数的性质,算术平方根的性质,绝对值的性质。
【分析】∵与|x﹣y﹣3|互为相反数,∴+|x﹣y﹣3|=0,
∴,解得。∴x+y=12+15=27。故选D。
9.如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )2·1·c·n·j·y
A.41 B.40 C.39 D.38
【答案】C。
【考点】正方体相对两个面上的文字。
【分析】∵三个骰子18个面上的数字的总和为:3(1+2+3+4+5+6)=3×21=63,
看得见的7个面上的数字的和为:1+2+3+5+4+6+3=24,
∴看不见的面上的点数总和是:63﹣24=39。故选C。
10.若,则m的值为( )
A.3 B.4 C.5 D. 6
【答案】A。
【考点】幂的乘方,同底数幂的乘法。
【分析】∵,∴,即,即。
∴1+5m=11,解得m=2。故选A。
二、填空题(每题4分,共24分)
1.计算:∣-2∣= ▲ ,= ▲ ,= ▲ ,=
▲ 。
【答案】2,,4,3。
【考点】绝对值,负整数指数幂,有理数的乘方,立方根化简。
【分析】根据乘法分配律,同底幂乘法,合并同类项,幂的乘方运算法则逐一计算即可。
2. 计算= ▲ .
【答案】。
【考点】有理数的减法,绝对值。
【分析】。
3.若x,y为实数,且满足,则的值是 ▲ .
【答案】1。
【考点】非负数的性质,算术平方根,绝对值。
【分析】根据算术平方根和绝对值非负数的性质,要使,必须有且,即x=3,y=3。∴。
4、实数m、n在数轴上的位置如图所示,则|n﹣m|= ▲ .
【答案】m﹣n。
【考点】实数与数轴。
【分析】如图可得:n<m,即n﹣m<0,∴|n﹣m|=﹣(n﹣m)=m﹣n。
5.计算= ▲ .
【答案】。
【考点】实数的运算,算术平方根,负整数指数幂,零指数幂。
【分析】针对算术平方根,负整数指数幂,零指数幂3个考点分别进行计算,然后根据实数的运算法则求得计算结果:。
6.已知整数满足下列条件:,,,
,…,依次类推,则的值为 .
A. B. C. D.
【答案】B。
【考点】分类归纳(数字的变化类)
【分析】根据条件求出前几个数的值,寻找规律,分是奇数和偶数讨论::
∵, ,
,,
,,
,,
…,
∴当是奇数时,,是偶数时, 。
∴。故选B。
三、解答题(17题6分,18题8分,23题12分,其余每题10分,共66分)
17.计算:.
【答案】解:原式=2+1-5+1+9=8。
【考点】实数的运算,算术平方根,零指数幂,绝对值,乘方,负整数指数幂。
【分析】针对算术平方根,零指数幂,绝对值,乘方,负整数指数幂5个考点分别进行计算,然后根据实数的运算法则求得计算结果。21世纪教育网版权所有
18.(1) (2)
(1)
(2)
19.把代表下列各数的序号填在相应的大括号内。
② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0)
整数集合: { -5 0 }
负分数集合:{ - 0.86 - }
无理数集合:{ 1.1010010001...(每两个1之间依次多一个0)}
实数:{ ② - 0.86 ; ③ -5; ④ 0; ⑤ -; ⑥; ⑦3.14;
⑧ ⑨ ⑩1.1010010001……(每两个1之间依次多一个0) }
20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;21cnjy.com
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
解:(1)64,8,15;
(2),,;
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
【答案】解:(1)。
(2)。
(3)a1+a2+a3+a4+…+a100
。
【考点】分类归纳(数字的变化类)。
【分析】(1)(2)观察知,找等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1。
(3)运用变化规律计算。
22.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
﹣2÷2=﹣1,
(2)请用你发现的规律求出图④中的数y和图⑤中的数x.
【答案】解:(1)填表如下:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
(﹣2)×(﹣5)×17=170
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
(﹣2)+(﹣5)+17=17
积与和的商
﹣2÷2=﹣1
(﹣60)÷(﹣12)=5
170÷10=17
(2)图④:∵5×(﹣8)×(﹣9)=360,5+(﹣8)+(﹣9)=﹣1,
∴y=360÷(﹣12)=﹣30。
图⑤:由(1·x·3)÷(1+x+3)=﹣3,解得x=﹣2。.
【考点】分类归纳(数字的变化类)。
【分析】(1)根据图形和表中已填写的形式,即可求出表中的空格;
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,列出方程,即可求出x、y的值。
23.请你规定一种适合任意非零实数a,b的新运算“a⊕b”,使得下列算式成立:
1⊕2=2⊕1=3,(﹣3)⊕(﹣4)=(﹣4)⊕(﹣3)=﹣,(﹣3)⊕5=5⊕(﹣3)=﹣,…
你规定的新运算a⊕b=?(用a,b的一个代数式表示).
【答案】。
【考点】分类归纳(数字的变化类),新定义。
【分析】寻找规律:
∵,
,···
∴。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
