浙教版数学七年级上册 6.9直线的相交 第二课时 课件(共20张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 6.9直线的相交 第二课时 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 739.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 06:30:53 | ||
图片预览



文档简介
(共20张PPT)
6.9 直线相交(二)
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解垂线的概念,会用符号表示两条直线互相垂直.
2. 会用三角尺或量角器过一已知点,画已知直线的垂线且只有一条直线.
3. 了解垂线段最短的性质,理解点到直线的距离的概念.
通过学习,培养学生学习的兴趣,渗透几何学的思想.
通过亲手操作,体会垂直是相交的一种特殊情况.
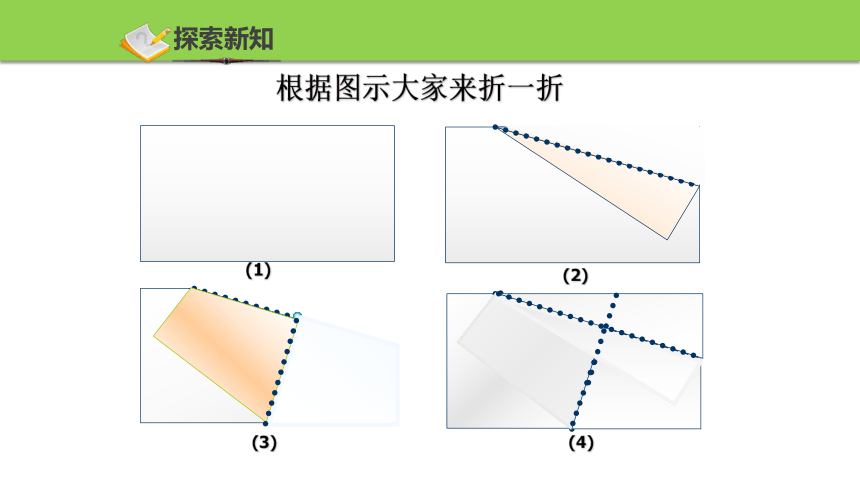
(1)
根据图示大家来折一折
(3)
(2)
(4)
探索新知
讲解新课
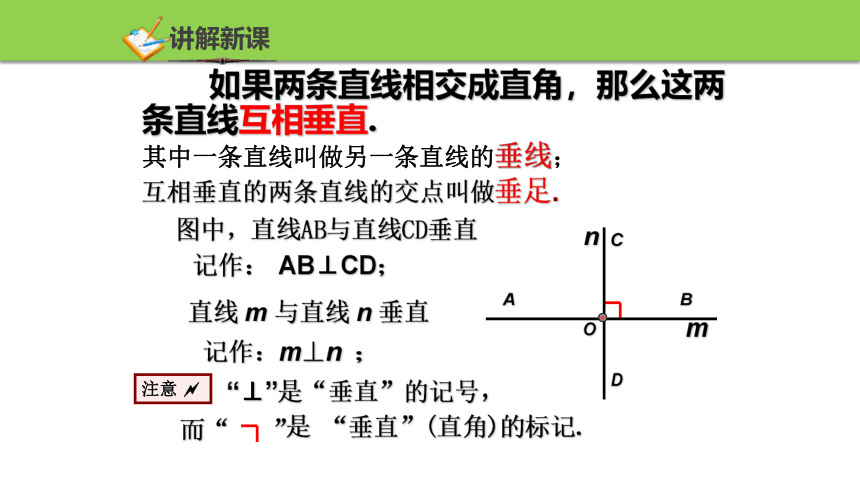
如果两条直线相交成直角,那么这两条直线互相垂直.
O
D
C
B
A
m
n
图中,直线AB与直线CD垂直
记作:
AB⊥CD;
直线 m 与直线 n 垂直
记作:m⊥n ;
互相垂直的两条直线的交点叫做垂足.
注意
“⊥”是“垂直”的记号,
而“ ”
是 “垂直”(直角)的标记.
其中一条直线叫做另一条直线的垂线;
新课讲解
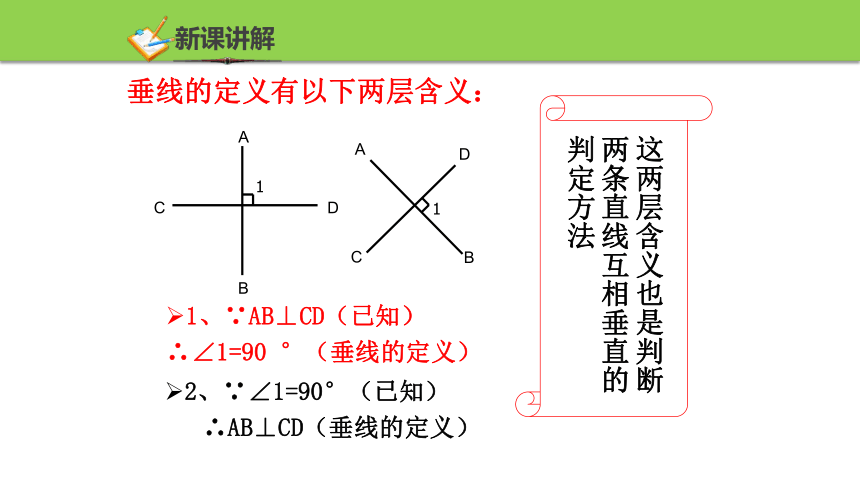
垂线的定义有以下两层含义:
1、∵AB⊥CD(已知)
∴∠1=90 °(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
A
B
C
D
1
A
B
C
D
1
这两层含义也是判断两条直线互相垂直的判定方法
0 1 2 3 4 5 6 7 8 9 10
新课讲解
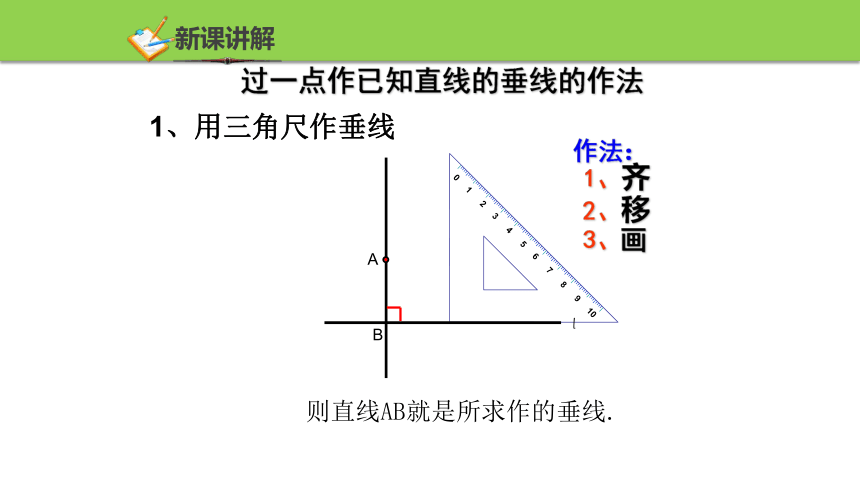
1、用三角尺作垂线
l
则直线AB就是所求作的垂线.
A
作法:
1、齐
2、移
3、画
B
过一点作已知直线的垂线的作法
新课讲解
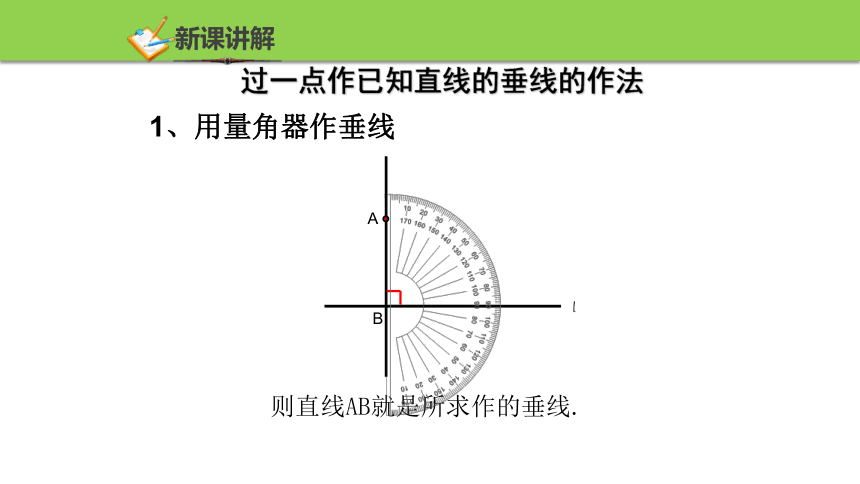
1、用量角器作垂线
l
则直线AB就是所求作的垂线.
A
B
过一点作已知直线的垂线的作法
做一做
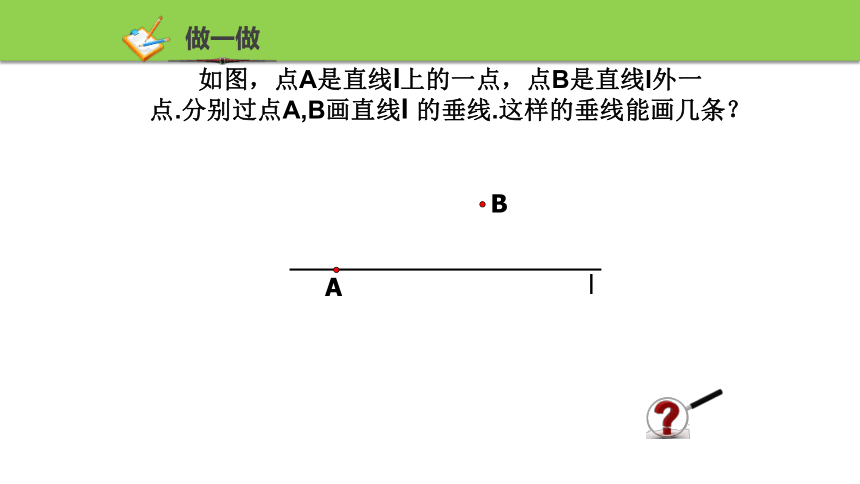
如图,点A是直线l上的一点,点B是直线l外一点.分别过点A,B画直线l 的垂线.这样的垂线能画几条?
B
A
l
新课讲解
垂线的性质:
在同一平面内,过一点有且仅有一条直线垂直于已知直线.
有而且
只有
例题分析
例1
如图直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠COE的度数.
A
B
O
D
C
E
解 ∵OE⊥AB
∴∠AOE=900 ( )
垂直的定义
∵∠AOC=∠BOD=450( )
∴∠COE=∠AOC+∠AOE=1350
对顶角相等
练一练
1、作一条直线l,
l
在l外取一点B,
A
在直线l上取一点A,
试分别过点A、B 用三角尺作直线的垂线.
B
0 1 2 3 4 5 6 7 8 9 10
C
D
则直线AC,直线BD就是所求作的垂线
练一练
2、如图,CD⊥EF,∠1= ∠ 2,则AB ⊥ EF,请说明理由(补全解答过程)
解 ∵ CD⊥EF
∴ ∠1=____( )
∵ ∠2= ∠ 1=____
∴ AB ⊥ EF
( )
两条直线互相垂直的意义
90°
90°
两条直线互相垂直的意义
C
E
1
D
B
A
F
2
合作学习
在直线L上任意选取点A1 , A2 , A3 ,……,B1 , B2 , B3 ,……,分别与点P连成线段P A1 ,P A2 ,P A3 ,……, P B1 ,P B2 ,P B3 ,……,哪个最小?
L
P
A1
o
A2
B3
B2
B1
A3
OP最小
L
P
A1
o
A2
B3
B2
B1
A3
OP是最小距离
垂线段
直线外一点与直线上各点连结的所有线段中,垂线段最短.
“垂线段最短”
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
垂线段的性质
点到直线的距离的概念
垂线段OP的长度,就是点P到直线L的距离.
新课讲解
练一练
(1)一条直线的垂线只能画一条( )
(2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
(3)点到直线的垂线段就是点到直线的距离( )
(4)过一点有且只有一条直线与已知直线垂( )
×
×
1.判断题
√
√
练一练
在下列图形中,线段PQ的长度表示点P到直线 的距离的是( )
P
Q
Q
P
Q
P
Q
P
(A)
(B)
(C)
(D)
C
2.选择题
拓展提高
l
B
1、如图,怎样测量点A 到直线l 的距离?
A
2、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:直线外一点与直线上各点连结的所有线段中,垂线段最短.
拓展提高
3、如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
小结
垂直定义;
垂线的多种画法;
垂直的表示方法;
垂直的性质;
点到直线的距离.
再见!
再见!
6.9 直线相交(二)
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解垂线的概念,会用符号表示两条直线互相垂直.
2. 会用三角尺或量角器过一已知点,画已知直线的垂线且只有一条直线.
3. 了解垂线段最短的性质,理解点到直线的距离的概念.
通过学习,培养学生学习的兴趣,渗透几何学的思想.
通过亲手操作,体会垂直是相交的一种特殊情况.
(1)
根据图示大家来折一折
(3)
(2)
(4)
探索新知
讲解新课
如果两条直线相交成直角,那么这两条直线互相垂直.
O
D
C
B
A
m
n
图中,直线AB与直线CD垂直
记作:
AB⊥CD;
直线 m 与直线 n 垂直
记作:m⊥n ;
互相垂直的两条直线的交点叫做垂足.
注意
“⊥”是“垂直”的记号,
而“ ”
是 “垂直”(直角)的标记.
其中一条直线叫做另一条直线的垂线;
新课讲解
垂线的定义有以下两层含义:
1、∵AB⊥CD(已知)
∴∠1=90 °(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
A
B
C
D
1
A
B
C
D
1
这两层含义也是判断两条直线互相垂直的判定方法
0 1 2 3 4 5 6 7 8 9 10
新课讲解
1、用三角尺作垂线
l
则直线AB就是所求作的垂线.
A
作法:
1、齐
2、移
3、画
B
过一点作已知直线的垂线的作法
新课讲解
1、用量角器作垂线
l
则直线AB就是所求作的垂线.
A
B
过一点作已知直线的垂线的作法
做一做
如图,点A是直线l上的一点,点B是直线l外一点.分别过点A,B画直线l 的垂线.这样的垂线能画几条?
B
A
l
新课讲解
垂线的性质:
在同一平面内,过一点有且仅有一条直线垂直于已知直线.
有而且
只有
例题分析
例1
如图直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠COE的度数.
A
B
O
D
C
E
解 ∵OE⊥AB
∴∠AOE=900 ( )
垂直的定义
∵∠AOC=∠BOD=450( )
∴∠COE=∠AOC+∠AOE=1350
对顶角相等
练一练
1、作一条直线l,
l
在l外取一点B,
A
在直线l上取一点A,
试分别过点A、B 用三角尺作直线的垂线.
B
0 1 2 3 4 5 6 7 8 9 10
C
D
则直线AC,直线BD就是所求作的垂线
练一练
2、如图,CD⊥EF,∠1= ∠ 2,则AB ⊥ EF,请说明理由(补全解答过程)
解 ∵ CD⊥EF
∴ ∠1=____( )
∵ ∠2= ∠ 1=____
∴ AB ⊥ EF
( )
两条直线互相垂直的意义
90°
90°
两条直线互相垂直的意义
C
E
1
D
B
A
F
2
合作学习
在直线L上任意选取点A1 , A2 , A3 ,……,B1 , B2 , B3 ,……,分别与点P连成线段P A1 ,P A2 ,P A3 ,……, P B1 ,P B2 ,P B3 ,……,哪个最小?
L
P
A1
o
A2
B3
B2
B1
A3
OP最小
L
P
A1
o
A2
B3
B2
B1
A3
OP是最小距离
垂线段
直线外一点与直线上各点连结的所有线段中,垂线段最短.
“垂线段最短”
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
垂线段的性质
点到直线的距离的概念
垂线段OP的长度,就是点P到直线L的距离.
新课讲解
练一练
(1)一条直线的垂线只能画一条( )
(2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
(3)点到直线的垂线段就是点到直线的距离( )
(4)过一点有且只有一条直线与已知直线垂( )
×
×
1.判断题
√
√
练一练
在下列图形中,线段PQ的长度表示点P到直线 的距离的是( )
P
Q
Q
P
Q
P
Q
P
(A)
(B)
(C)
(D)
C
2.选择题
拓展提高
l
B
1、如图,怎样测量点A 到直线l 的距离?
A
2、如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由.
张庄
∟
理由:直线外一点与直线上各点连结的所有线段中,垂线段最短.
拓展提高
3、如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。
C
∟
垂线段最短
小结
垂直定义;
垂线的多种画法;
垂直的表示方法;
垂直的性质;
点到直线的距离.
再见!
再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
