浙教版数学七年级上册 6.8余角和补角 课件(共20张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 6.8余角和补角 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 651.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
6.8 余角和补角
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解补角和余角的概念.
2.理解等角的余角相等,等角的补角相等.
3.了解角在解决实际问题中的一些简单应用.
能根据互为补角、互为余角的重要特征解决几何中的一些简单问题.
学会运用类比联想的思维方法思考,并初步学会用代数的方法解决几何问题.
引入新课
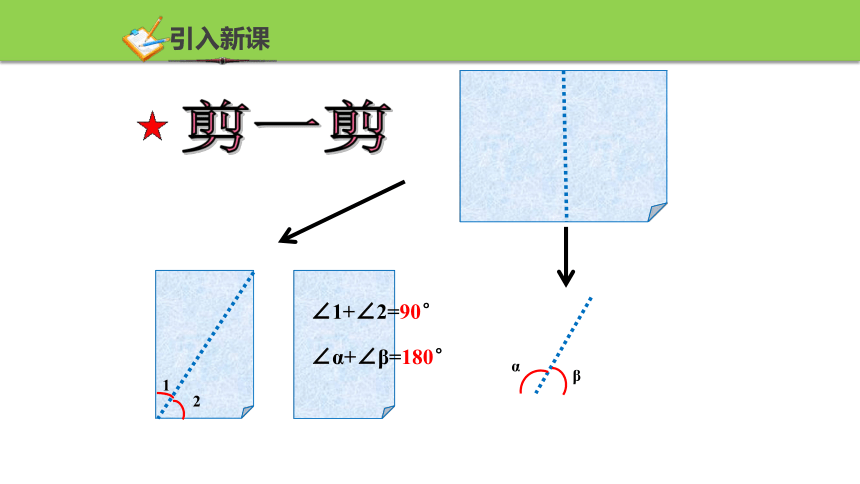
剪一剪
1
2
α
β
∠1+∠2=90°
∠α+∠β=180°
讲解新课
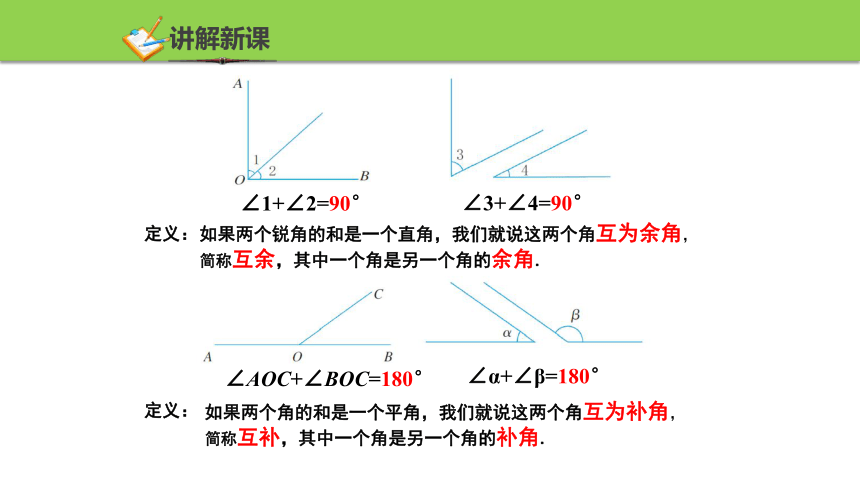
∠1+∠2=90°
∠3+∠4=90°
∠AOC+∠BOC=180°
∠α+∠β=180°
如果两个锐角的和是一个直角,我们就说这两个角互为余角, 简称互余,其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,
简称互补,其中一个角是另一个角的补角.
定义:
定义:
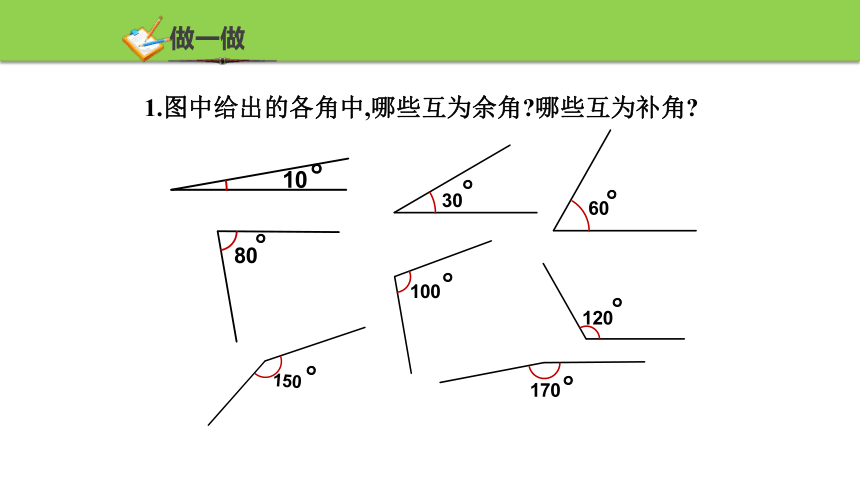
1.图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
做一做
做一做
2.如图,吊桥与铅垂方向所成的角∠α=30°.若要把吊桥放平,则吊桥需沿什么方向转动?转动多少度的角?
30°
做一做
3.填空:
(1)∠α的余角=90°-_______.
(2)的余角=_______-∠ β.
当∠α=∠β时,就有∠α的余角与∠β的余角相等
新课讲解
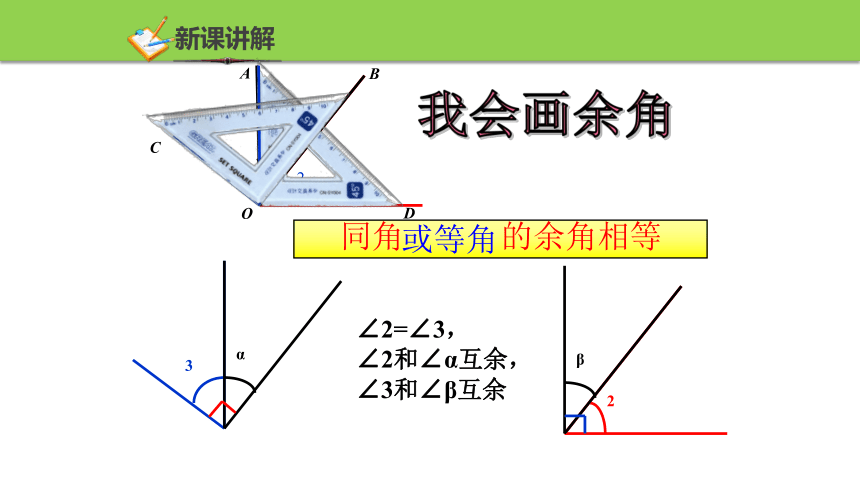
∠2=∠3,
∠2和∠α互余,
∠3和∠β互余
C
D
2
3
1
O
A
B
3
2
β
α
同角 的余角相等
或等角
我会画余角
新课讲解
1
∠2=∠3,∠2和∠α互补,∠3和∠β互补
C
D
2
3
O
A
B
α
β
同角 的补角相等 .
或等角
2
3
我会画补角
例题分析
例1 如图∠AOC = 90°,∠BOD = 90°则∠1与∠2是什么关系?
∠1=∠2
A
O
B
C
D
1
2
解
∴∠1+∠BOD=90°
∠2+∠BOD=90°
∴∠1=∠2
∵∠AOB =∠COD =90°
(同角的余角相等)
练一练
4.如图,直线CD经过点O,且OC平分∠AOB.试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
解:∠AOD=∠BOD
∵∠AOD与∠AOC互补, ∠BOD与∠BOC互补
∴∠AOD=180°-∠AOC
∠BOD=180°-∠BOC
又∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC=∠BOC
例题分析
例2 已知一个角的补角是这个角的余角的4倍,求这个角的度数.
解
设这个角是x °
则它的余角是(90-x) °,补角是(180-x)°
由题意得:
(180-x )°= 4 (90-x)°
解得:x =60
答:这个角的度数是60 °.
练一练
5.已知两个角互为补角,它们的差为30 °,求这两个角的度数.
随 堂 作 业
拓展提高
6.判断:
(1)互余的两个角必定都是锐角.
(2)一个角的补角必定是钝角.
(3)两个角互补,那么这两个角中,
必定一个是锐角,另一个是钝角.
拓展提高
∠α ∠α的余角 ∠α的补角
5° 85° 175°
32° 58° 148°
45° 45° 135°
77° 13° 103°
62°23′ 27°37′ 117°37′
x 90°-x 180°-x
90°-β β β+90°
8.∠1=120°, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
拓展提高
30°
9.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90°
则∠BOC = ,
∠COD = .
拓展提高
A
O
B
E
D
C
∠DOE
∠AOE
小结
互余的角 互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
1+ 2=90°
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
再见!
再见!
6.8 余角和补角
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解补角和余角的概念.
2.理解等角的余角相等,等角的补角相等.
3.了解角在解决实际问题中的一些简单应用.
能根据互为补角、互为余角的重要特征解决几何中的一些简单问题.
学会运用类比联想的思维方法思考,并初步学会用代数的方法解决几何问题.
引入新课
剪一剪
1
2
α
β
∠1+∠2=90°
∠α+∠β=180°
讲解新课
∠1+∠2=90°
∠3+∠4=90°
∠AOC+∠BOC=180°
∠α+∠β=180°
如果两个锐角的和是一个直角,我们就说这两个角互为余角, 简称互余,其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,
简称互补,其中一个角是另一个角的补角.
定义:
定义:
1.图中给出的各角中,哪些互为余角 哪些互为补角
°
°
°
°
°
°
°
°
做一做
做一做
2.如图,吊桥与铅垂方向所成的角∠α=30°.若要把吊桥放平,则吊桥需沿什么方向转动?转动多少度的角?
30°
做一做
3.填空:
(1)∠α的余角=90°-_______.
(2)的余角=_______-∠ β.
当∠α=∠β时,就有∠α的余角与∠β的余角相等
新课讲解
∠2=∠3,
∠2和∠α互余,
∠3和∠β互余
C
D
2
3
1
O
A
B
3
2
β
α
同角 的余角相等
或等角
我会画余角
新课讲解
1
∠2=∠3,∠2和∠α互补,∠3和∠β互补
C
D
2
3
O
A
B
α
β
同角 的补角相等 .
或等角
2
3
我会画补角
例题分析
例1 如图∠AOC = 90°,∠BOD = 90°则∠1与∠2是什么关系?
∠1=∠2
A
O
B
C
D
1
2
解
∴∠1+∠BOD=90°
∠2+∠BOD=90°
∴∠1=∠2
∵∠AOB =∠COD =90°
(同角的余角相等)
练一练
4.如图,直线CD经过点O,且OC平分∠AOB.试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
解:∠AOD=∠BOD
∵∠AOD与∠AOC互补, ∠BOD与∠BOC互补
∴∠AOD=180°-∠AOC
∠BOD=180°-∠BOC
又∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC=∠BOC
例题分析
例2 已知一个角的补角是这个角的余角的4倍,求这个角的度数.
解
设这个角是x °
则它的余角是(90-x) °,补角是(180-x)°
由题意得:
(180-x )°= 4 (90-x)°
解得:x =60
答:这个角的度数是60 °.
练一练
5.已知两个角互为补角,它们的差为30 °,求这两个角的度数.
随 堂 作 业
拓展提高
6.判断:
(1)互余的两个角必定都是锐角.
(2)一个角的补角必定是钝角.
(3)两个角互补,那么这两个角中,
必定一个是锐角,另一个是钝角.
拓展提高
∠α ∠α的余角 ∠α的补角
5° 85° 175°
32° 58° 148°
45° 45° 135°
77° 13° 103°
62°23′ 27°37′ 117°37′
x 90°-x 180°-x
90°-β β β+90°
8.∠1=120°, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
拓展提高
30°
9.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90°
则∠BOC = ,
∠COD = .
拓展提高
A
O
B
E
D
C
∠DOE
∠AOE
小结
互余的角 互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
1+ 2=90°
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
再见!
再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
