浙教版数学七年级上册 6.4 线段的和差 课件 (共23张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 6.4 线段的和差 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 525.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 20:21:12 | ||
图片预览






文档简介
(共22张PPT)
6.4 线段的和差
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解线段和、差的概念.
2.会画两条线段的和差.
3.理解线段的中点的概念,会利用刻度尺画线段的中点.
通过线段的和、差、倍、分等计算,初步养成简单的判断和推理能力.
体会数形结合的思想,感受几何的魅力.
知识回顾
a
C
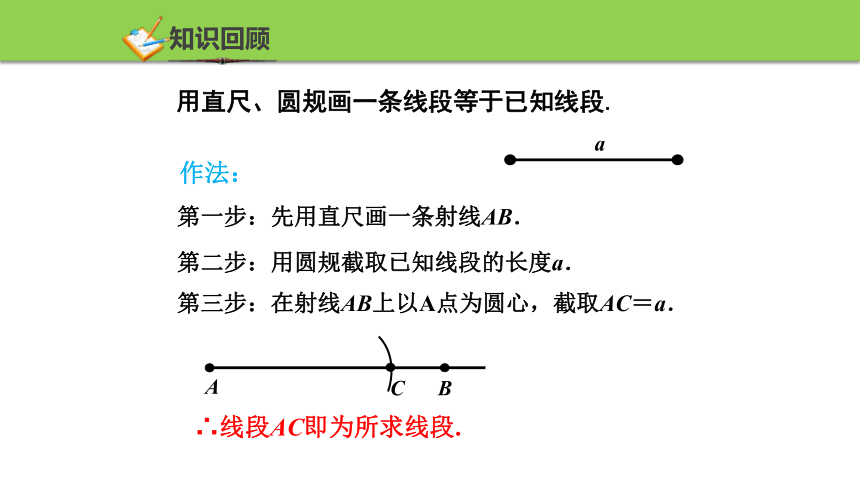
∴线段AC即为所求线段.
第一步:先用直尺画一条射线AB.
第二步:用圆规截取已知线段的长度a.
第三步:在射线AB上以A点为圆心,截取AC=a.
A
B
用直尺、圆规画一条线段等于已知线段.
作法:
新课引入
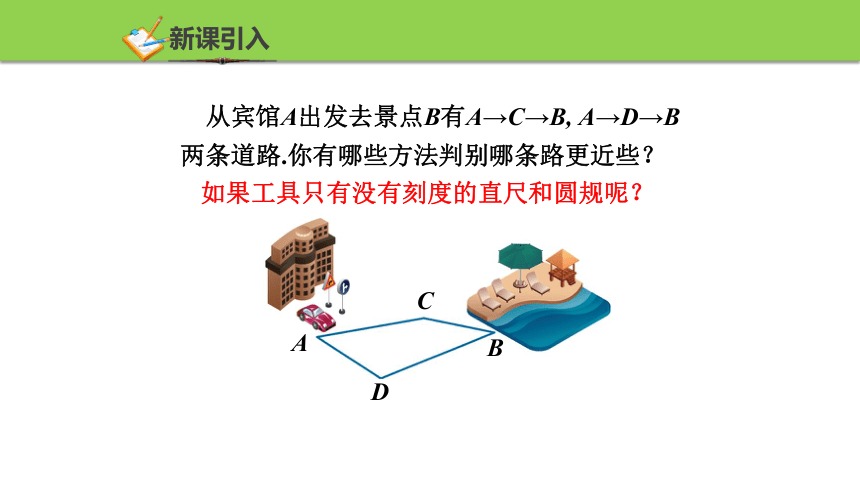
从宾馆A出发去景点B有A→C→B, A→D→B两条道路.你有哪些方法判别哪条路更近些?
如果工具只有没有刻度的直尺和圆规呢?
A
B
C
D
新课讲解
如图,已知线段a=1.5cm,b=2.5cm,c=4cm.
a
b
c
a,b,c三条线段之间的长度有什么关系?
∵ 1.5+2.5=4
线段c的长度是线段a与b的长度的和,我们就说线段c是线段a与b的和,
记作:c=a+b
新课讲解
如图,已知线段a=1.5cm,b=2.5cm,c=4cm.
a
b
c
a,b,c三条线段之间的长度有什么关系?
∵ 4-2.5=1.5
线段a的长度是线段c与b的长度的差,我们就说线段a是线段c与b的差,
记作:a=c-b
两条线段的和或差,仍是一条线段.
练一练
练习:如图,C是线段AB上的一点.请完成下面的填空.
C
B
A
D
AB+BC = ______
AC
AD-CD=______
AC
BC=_____-AB
AC
CD
= BD-______
例题讲解
例1
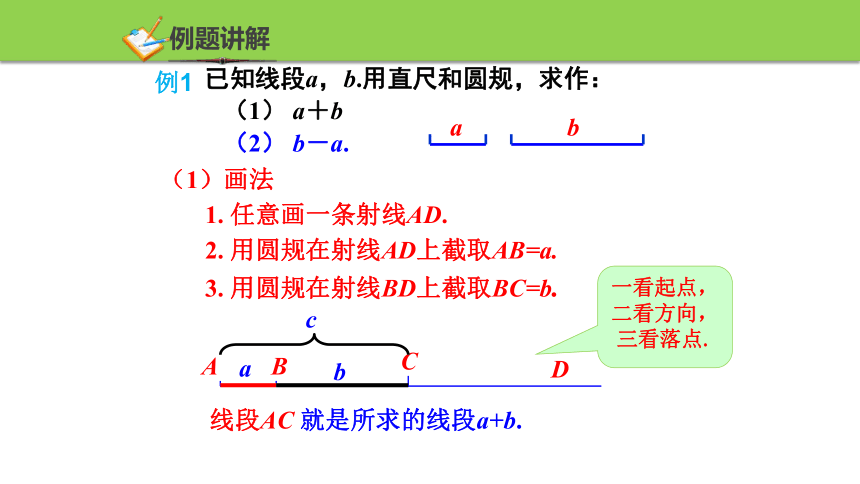
已知线段a,b.用直尺和圆规,求作:
(1) a+b
(2) b-a.
a
b
b
(1)画法
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC 就是所求的线段a+b.
c
一看起点,二看方向,
三看落点.
例题讲解
例1
已知线段a,b.用直尺和圆规,求作:
(1) a+b
(2) b-a.
b
(2)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=b.
3. 用圆规在射线AB上截取AB=a.
a
A
D
B
C
线段BC 就是所求的线段b-a.
a
b
练一练
练习:已知:如图,直线l上有A、B、C三点,且线段AB=8cm,线段BC=5cm,求线段AC的长.
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
l
A
B
C
l
A
B
C
新课讲解
A
B
C
观察下列步骤,并回答问题
(1)拿出一张白纸,对折这张白纸.
(2)把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
点C把线段AB分成相等的两条线段
AC和BC,点C叫做线段AB的中点.
点C具有什么特殊的位置?
请你给它起一个名字,并描述这一位置的特征.
定义
练一练
练习:用刻度尺画线段AB的中点.
B
A
例题讲解
例2 如图,P是线段AE的中点,点C,D把线段AE三等分.已知线段CP的长为1.5 cm,求线段AE的长.
练一练
练习:1.如果AC=4,求AB、BC.
A
B
C
解:∵点B是线段AC的中点,
∴AB=BC= AC.
∵AC=4,
∴AB=BC= ×4=2.
(线段中点定义)
(已知)
(已知)
练一练
2.如图,已知C是线段AB的中点,点D是线段AC的中点.
请完成下列填空.
(1) AB = BC .
(2) AD = AC .
(3) BD = AD .
2
1
2
3
随 堂 作 业
拓展提高
1.已知线段AB=a,延长BA至点C,使
AC= AB.D为线段BC的中点.
(1) 求CD的长.
(2) 若AD=3cm,求a的值.
1
2
1
2
a
a
3
4
a
3
4
a
1
4
a
拓展提高
2.若点P在线段AB上,E、F分别是AP和BP的中点.
(1)若AP=8,BP=6,求线段EF的长;
A
B
P
E
F
4
3
8
6
拓展提高
A
B
P
E
F
a
b
1
2
a
1
2
b
从特殊到一般
2.若点P在线段AB上,E、F分别是AP和BP的中点.
(2)若线段AP=a,BP=b,求线段EF的长.
拓展提高
A
B
P
E
F
a
b
1
2
a
1
2
b
(3)若点P在线段AB的延长线上, E、F分别是AP和BP的中点. 线段AP=a,BP=b,
线段EF的长有变化吗? 请你通过计算说明.
小结
2.画两条线段的和差.
1.线段的和差概念.
3.线段的中点的概念.
4.用刻度尺画线段的中点.
5.线段和、差、倍、分的计算.
再见!
再见!
6.4 线段的和差
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1. 了解线段和、差的概念.
2.会画两条线段的和差.
3.理解线段的中点的概念,会利用刻度尺画线段的中点.
通过线段的和、差、倍、分等计算,初步养成简单的判断和推理能力.
体会数形结合的思想,感受几何的魅力.
知识回顾
a
C
∴线段AC即为所求线段.
第一步:先用直尺画一条射线AB.
第二步:用圆规截取已知线段的长度a.
第三步:在射线AB上以A点为圆心,截取AC=a.
A
B
用直尺、圆规画一条线段等于已知线段.
作法:
新课引入
从宾馆A出发去景点B有A→C→B, A→D→B两条道路.你有哪些方法判别哪条路更近些?
如果工具只有没有刻度的直尺和圆规呢?
A
B
C
D
新课讲解
如图,已知线段a=1.5cm,b=2.5cm,c=4cm.
a
b
c
a,b,c三条线段之间的长度有什么关系?
∵ 1.5+2.5=4
线段c的长度是线段a与b的长度的和,我们就说线段c是线段a与b的和,
记作:c=a+b
新课讲解
如图,已知线段a=1.5cm,b=2.5cm,c=4cm.
a
b
c
a,b,c三条线段之间的长度有什么关系?
∵ 4-2.5=1.5
线段a的长度是线段c与b的长度的差,我们就说线段a是线段c与b的差,
记作:a=c-b
两条线段的和或差,仍是一条线段.
练一练
练习:如图,C是线段AB上的一点.请完成下面的填空.
C
B
A
D
AB+BC = ______
AC
AD-CD=______
AC
BC=_____-AB
AC
CD
= BD-______
例题讲解
例1
已知线段a,b.用直尺和圆规,求作:
(1) a+b
(2) b-a.
a
b
b
(1)画法
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC 就是所求的线段a+b.
c
一看起点,二看方向,
三看落点.
例题讲解
例1
已知线段a,b.用直尺和圆规,求作:
(1) a+b
(2) b-a.
b
(2)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=b.
3. 用圆规在射线AB上截取AB=a.
a
A
D
B
C
线段BC 就是所求的线段b-a.
a
b
练一练
练习:已知:如图,直线l上有A、B、C三点,且线段AB=8cm,线段BC=5cm,求线段AC的长.
AC=AB+BC
=8+5=13cm
AC=AB-BC
=8-5=3cm
l
A
B
C
l
A
B
C
新课讲解
A
B
C
观察下列步骤,并回答问题
(1)拿出一张白纸,对折这张白纸.
(2)把白纸展开铺平,发现在边AB上有个折痕点C,请问AC和BC相等吗?
点C把线段AB分成相等的两条线段
AC和BC,点C叫做线段AB的中点.
点C具有什么特殊的位置?
请你给它起一个名字,并描述这一位置的特征.
定义
练一练
练习:用刻度尺画线段AB的中点.
B
A
例题讲解
例2 如图,P是线段AE的中点,点C,D把线段AE三等分.已知线段CP的长为1.5 cm,求线段AE的长.
练一练
练习:1.如果AC=4,求AB、BC.
A
B
C
解:∵点B是线段AC的中点,
∴AB=BC= AC.
∵AC=4,
∴AB=BC= ×4=2.
(线段中点定义)
(已知)
(已知)
练一练
2.如图,已知C是线段AB的中点,点D是线段AC的中点.
请完成下列填空.
(1) AB = BC .
(2) AD = AC .
(3) BD = AD .
2
1
2
3
随 堂 作 业
拓展提高
1.已知线段AB=a,延长BA至点C,使
AC= AB.D为线段BC的中点.
(1) 求CD的长.
(2) 若AD=3cm,求a的值.
1
2
1
2
a
a
3
4
a
3
4
a
1
4
a
拓展提高
2.若点P在线段AB上,E、F分别是AP和BP的中点.
(1)若AP=8,BP=6,求线段EF的长;
A
B
P
E
F
4
3
8
6
拓展提高
A
B
P
E
F
a
b
1
2
a
1
2
b
从特殊到一般
2.若点P在线段AB上,E、F分别是AP和BP的中点.
(2)若线段AP=a,BP=b,求线段EF的长.
拓展提高
A
B
P
E
F
a
b
1
2
a
1
2
b
(3)若点P在线段AB的延长线上, E、F分别是AP和BP的中点. 线段AP=a,BP=b,
线段EF的长有变化吗? 请你通过计算说明.
小结
2.画两条线段的和差.
1.线段的和差概念.
3.线段的中点的概念.
4.用刻度尺画线段的中点.
5.线段和、差、倍、分的计算.
再见!
再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
