浙教版七年级上册5.2等式的基本性质 课件(共25张PPT)
文档属性
| 名称 | 浙教版七年级上册5.2等式的基本性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 659.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 23:07:41 | ||
图片预览




文档简介
(共25张PPT)
5.2 等式的基本性质
义务教育课程标准实验教科书
浙教版《数学》七年级上册
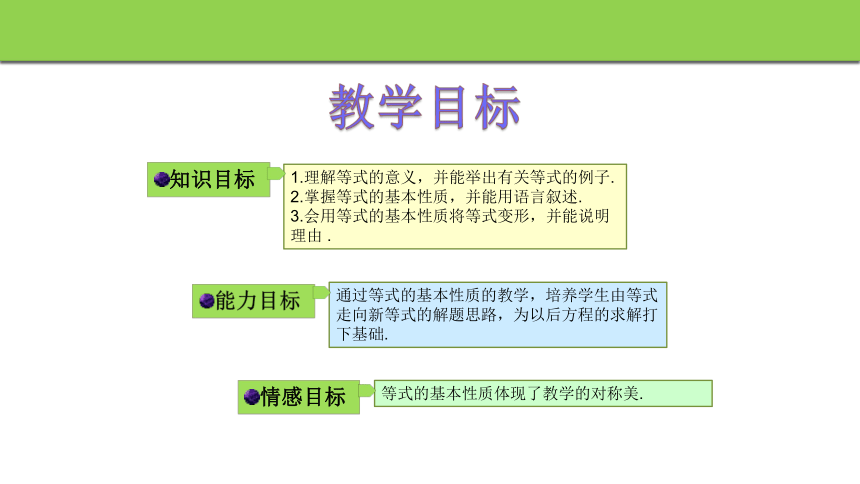
教学目标
知识目标
1.理解等式的意义,并能举出有关等式的例子.
2.掌握等式的基本性质,并能用语言叙述.
3.会用等式的基本性质将等式变形,并能说明理由 .
情感目标
等式的基本性质体现了教学的对称美.
能力目标
通过等式的基本性质的教学,培养学生由等式走向新等式的解题思路,为以后方程的求解打下基础.
1.什么是等式?
像这样用等号“=”表示相等关系的式子叫等式.
知识回顾
A.3个 B.4个 C.5个 D.6个
2.下列式子中是等式的有( ).
C
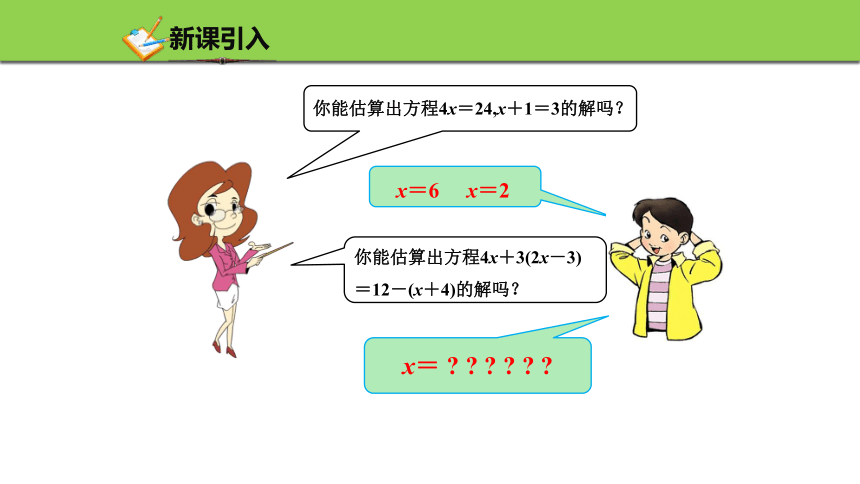
x=6
x=2
你能估算出方程4x=24,x+1=3的解吗?
你能估算出方程4x+3(2x-3)
=12-(x+4)的解吗?
x=
新课引入
a
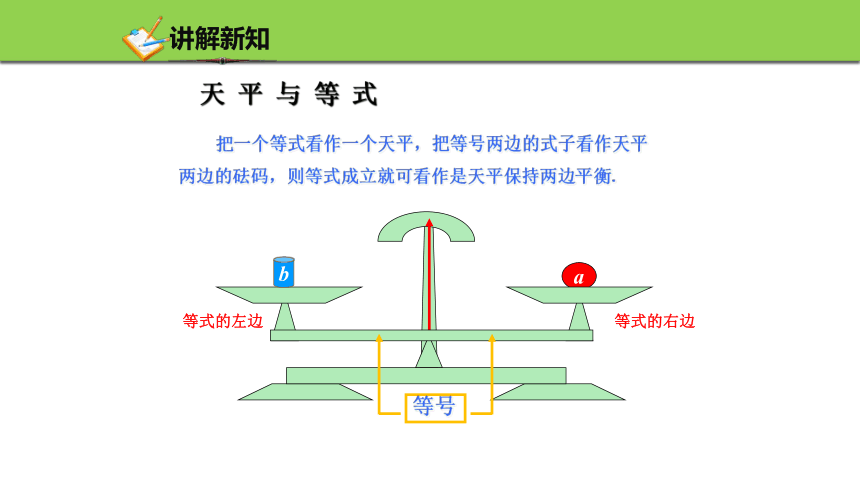
天 平 与 等 式
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
等式的左边
等式的右边
等号
b
讲解新知
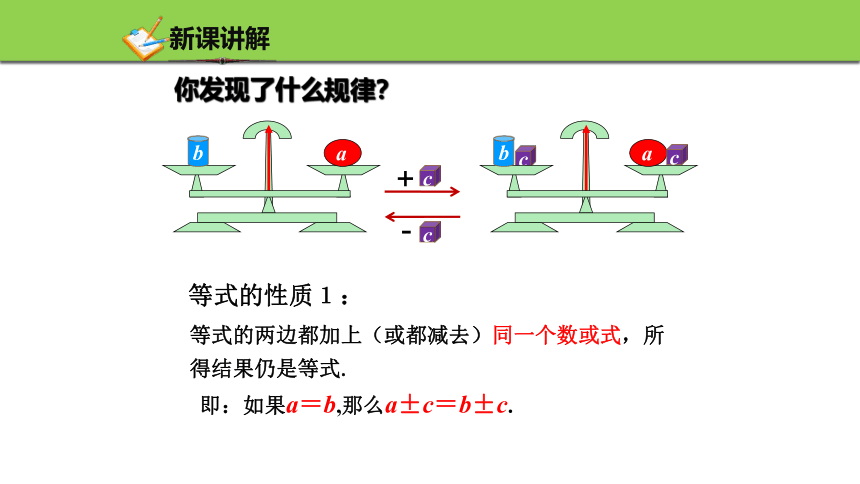
你发现了什么规律?
c
a
b
a
b
c
等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
等式的性质1:
即:如果a=b,那么a±c=b±c.
+
c
-
c
新课讲解
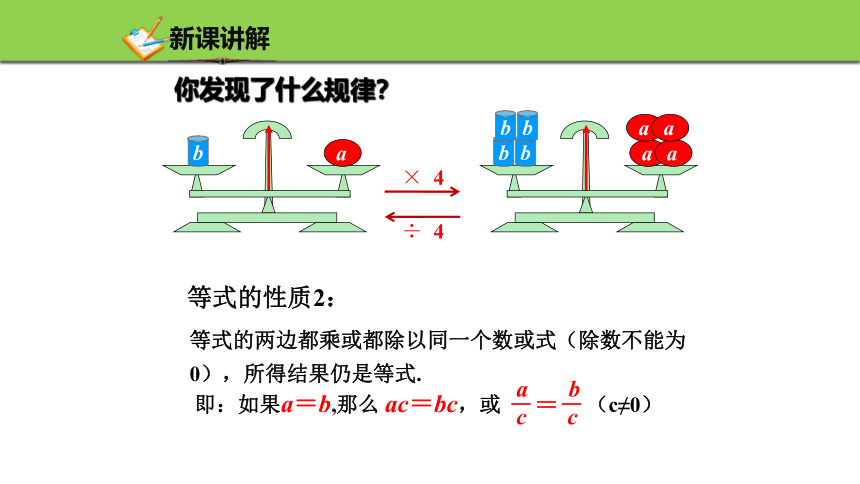
你发现了什么规律?
a
b
a
b
等式的性质2:
× 4
÷ 4
等式的两边都乘或都除以同一个数或式(除数不能为0),所得结果仍是等式.
b
a
b
b
a
a
新课讲解
即:如果a=b,那么 ac=bc,或 (c≠0)
a b
c c
-=-
1.下列变形符合等式性质的( )
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=1,那么3x=1-2
C.如果-2x=5,那么x=5+2
D
D.如果--x=1,那么x=-3
1
3
做一做
D
2.依据等式性质进行变形,用得不正确的是( ).
A.如果x+y=5,那么x=5-y
B.如果x+y=5,那么x+y-5=0
C.如果x+y=5,那么-(x+y)=-
1
2
5
2
D.如果x+y=5,那么 =-
x+y
a
5
a
做一做
3.下列说法错误的有( ).
做一做
A.2个 B.3个 C.4个 D.5个
B
4.填空.
(1)如果-x=0.5,那么2×-x=_________.
根据 _________________________________.
(2) 如果x-3=2,那么x-3+3=_________,
根据_________________________________.
(3) 如果4x=-12y,那么x=_______,
根据__________________________________ .
(4) 如果-0.2x=6,那么x=_______,
根据____________________________________ .
1
2
1
2
2×0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除-0.2或乘-5
做一做
注意
(1)等式两边都要参加运算,且是同一种运算.
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能都除以0,即0不能作除数或分母.
新课讲解
例1 已知2x-5y=0,且y≠0,判断下列等式是否成立,并说明理由.
解:
(1)成立,理由如下:
已知2x-5y=0,
两边都加上5y,得
2x-5y+5y=0+5y
∴2x=5y
(等式的性质1)
(2)成立,理由如下:
由(1)知2x=5y,而y≠0,
两边都除以2y,得
(等式的性质2)
例题讲解
求方程的解,就是通过对原方程的一系列变形(两边同加减、乘除),最终把方程化为 “x = a(a为已知数)的形式.
等式的性质是方程变形的依据.
新课讲解
例2 利用等式的性质解下列方程:
(1)5x=50+4x
方程的两边都减去4x,得5x-4x=50+4x-4x
合并同类项,得 x=50
检验:把x=50带入方程得:
左边=250 ;右边=250
∵左边=右边
∴x=50是原方程的解.
(等式的性质1)
例题讲解
解:(1)
例2 利用等式的性质解下列方程:
(1)5x=50+4x
检验:
例题讲解
(2) 8 -2x=9-4x
解:(2)
方程的两边都加上4x,得 8-2x+4x=9-4x+4x
合并同类项,得 8+2x=9
两边都减去8,得 2x=1
两边都除以2,得 x=0.5
把x=0.5代入原方程,
左边=8-2×0.5=7 右边=9-4×0.5=7
∵左边=右边
∴x=0.5是原方程的解
(等式的性质2)
(等式的性质1)
(等式的性质1)
(1)先利用等式性质1把方程变形为左边只含有未知数,右边只含有常数的形式.
(2)再利用等式性质2把方程变形为x =?的形式.
解方程的基本思路
新课讲解
5.利用等式的性质解下列方程
x=150
x=-0.8
x=8
做一做
随 堂 检 测
6.已知x+3=1,下列等式成立吗?根据什么?
等式性质2,在等式两边同时乘(-2)
等式性质1,在等式两边同减x
等式性质2,在等式两边同时除以3
成立
成立
成立
等式性质1,在等式两边同减3
成立
拓展提高
7.在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:
3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a (等式两边同时减去b)
3=7 (等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来.
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
拓展提高
8. 已知 x=1 是方程 的解,求a.
拓展提高
小结
等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
1.等式的性质1:
即:如果a=b,那么a±c=b±c.
2.等式的性质2:
等式的两边都乘或都除以同一个数或式(除数不能为0),所得结果仍是等式.
即:如果a=b,那么 ac=bc,或-=- (c≠0)
a b
c c
小结
(1)先利用等式性质1把方程变形为左边只含有未知数,右边只含有常数的形式.
(2)再利用等式性质2把方程变形为x =?的形式.
3.解方程的基本思路
再见!
再见!
5.2 等式的基本性质
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
1.理解等式的意义,并能举出有关等式的例子.
2.掌握等式的基本性质,并能用语言叙述.
3.会用等式的基本性质将等式变形,并能说明理由 .
情感目标
等式的基本性质体现了教学的对称美.
能力目标
通过等式的基本性质的教学,培养学生由等式走向新等式的解题思路,为以后方程的求解打下基础.
1.什么是等式?
像这样用等号“=”表示相等关系的式子叫等式.
知识回顾
A.3个 B.4个 C.5个 D.6个
2.下列式子中是等式的有( ).
C
x=6
x=2
你能估算出方程4x=24,x+1=3的解吗?
你能估算出方程4x+3(2x-3)
=12-(x+4)的解吗?
x=
新课引入
a
天 平 与 等 式
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡.
等式的左边
等式的右边
等号
b
讲解新知
你发现了什么规律?
c
a
b
a
b
c
等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
等式的性质1:
即:如果a=b,那么a±c=b±c.
+
c
-
c
新课讲解
你发现了什么规律?
a
b
a
b
等式的性质2:
× 4
÷ 4
等式的两边都乘或都除以同一个数或式(除数不能为0),所得结果仍是等式.
b
a
b
b
a
a
新课讲解
即:如果a=b,那么 ac=bc,或 (c≠0)
a b
c c
-=-
1.下列变形符合等式性质的( )
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=1,那么3x=1-2
C.如果-2x=5,那么x=5+2
D
D.如果--x=1,那么x=-3
1
3
做一做
D
2.依据等式性质进行变形,用得不正确的是( ).
A.如果x+y=5,那么x=5-y
B.如果x+y=5,那么x+y-5=0
C.如果x+y=5,那么-(x+y)=-
1
2
5
2
D.如果x+y=5,那么 =-
x+y
a
5
a
做一做
3.下列说法错误的有( ).
做一做
A.2个 B.3个 C.4个 D.5个
B
4.填空.
(1)如果-x=0.5,那么2×-x=_________.
根据 _________________________________.
(2) 如果x-3=2,那么x-3+3=_________,
根据_________________________________.
(3) 如果4x=-12y,那么x=_______,
根据__________________________________ .
(4) 如果-0.2x=6,那么x=_______,
根据____________________________________ .
1
2
1
2
2×0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除-0.2或乘-5
做一做
注意
(1)等式两边都要参加运算,且是同一种运算.
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能都除以0,即0不能作除数或分母.
新课讲解
例1 已知2x-5y=0,且y≠0,判断下列等式是否成立,并说明理由.
解:
(1)成立,理由如下:
已知2x-5y=0,
两边都加上5y,得
2x-5y+5y=0+5y
∴2x=5y
(等式的性质1)
(2)成立,理由如下:
由(1)知2x=5y,而y≠0,
两边都除以2y,得
(等式的性质2)
例题讲解
求方程的解,就是通过对原方程的一系列变形(两边同加减、乘除),最终把方程化为 “x = a(a为已知数)的形式.
等式的性质是方程变形的依据.
新课讲解
例2 利用等式的性质解下列方程:
(1)5x=50+4x
方程的两边都减去4x,得5x-4x=50+4x-4x
合并同类项,得 x=50
检验:把x=50带入方程得:
左边=250 ;右边=250
∵左边=右边
∴x=50是原方程的解.
(等式的性质1)
例题讲解
解:(1)
例2 利用等式的性质解下列方程:
(1)5x=50+4x
检验:
例题讲解
(2) 8 -2x=9-4x
解:(2)
方程的两边都加上4x,得 8-2x+4x=9-4x+4x
合并同类项,得 8+2x=9
两边都减去8,得 2x=1
两边都除以2,得 x=0.5
把x=0.5代入原方程,
左边=8-2×0.5=7 右边=9-4×0.5=7
∵左边=右边
∴x=0.5是原方程的解
(等式的性质2)
(等式的性质1)
(等式的性质1)
(1)先利用等式性质1把方程变形为左边只含有未知数,右边只含有常数的形式.
(2)再利用等式性质2把方程变形为x =?的形式.
解方程的基本思路
新课讲解
5.利用等式的性质解下列方程
x=150
x=-0.8
x=8
做一做
随 堂 检 测
6.已知x+3=1,下列等式成立吗?根据什么?
等式性质2,在等式两边同时乘(-2)
等式性质1,在等式两边同减x
等式性质2,在等式两边同时除以3
成立
成立
成立
等式性质1,在等式两边同减3
成立
拓展提高
7.在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:
3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a (等式两边同时减去b)
3=7 (等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来.
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
拓展提高
8. 已知 x=1 是方程 的解,求a.
拓展提高
小结
等式的两边都加上(或都减去)同一个数或式,所得结果仍是等式.
1.等式的性质1:
即:如果a=b,那么a±c=b±c.
2.等式的性质2:
等式的两边都乘或都除以同一个数或式(除数不能为0),所得结果仍是等式.
即:如果a=b,那么 ac=bc,或-=- (c≠0)
a b
c c
小结
(1)先利用等式性质1把方程变形为左边只含有未知数,右边只含有常数的形式.
(2)再利用等式性质2把方程变形为x =?的形式.
3.解方程的基本思路
再见!
再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
