2.3有理数的乘法 第二课时 课件(共26张PPT) 浙教版数学七年级上
文档属性
| 名称 | 2.3有理数的乘法 第二课时 课件(共26张PPT) 浙教版数学七年级上 |  | |
| 格式 | pptx | ||
| 文件大小 | 609.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 12:33:21 | ||
图片预览







文档简介
(共26张PPT)
2.3 有理数的乘法(二)
义务教育课程标准实验教科书
浙教版《数学》七年级上册
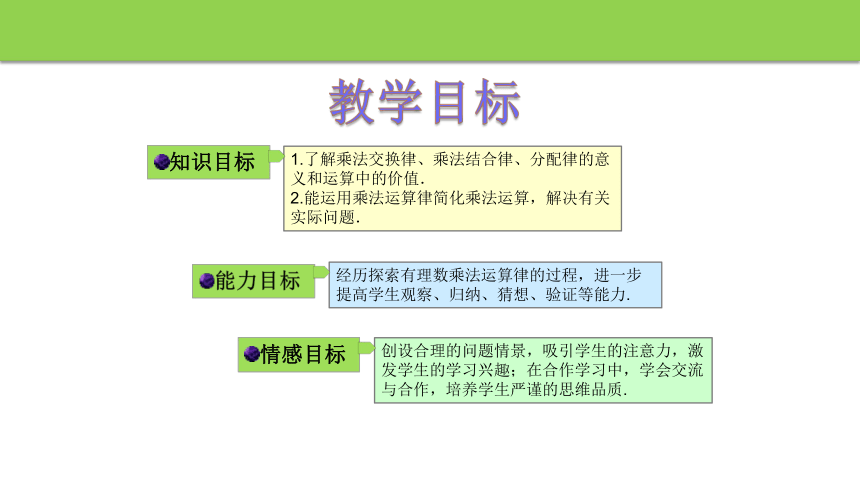
教学目标
知识目标
能力目标
情感目标
1.了解乘法交换律、乘法结合律、分配律的意义和运算中的价值.
2.能运用乘法运算律简化乘法运算,解决有关实际问题.
经历探索有理数乘法运算律的过程,进一步提高学生观察、归纳、猜想、验证等能力.
创设合理的问题情景,吸引学生的注意力,激发学生的学习兴趣;在合作学习中,学会交流与合作,培养学生严谨的思维品质.
1.有理数的乘法法则:
任何数与0相乘,积为0.
知识回顾
两数相乘,同号得正,异号得负,并把绝对值相乘.
2.多个不为0的有理数相乘,积的符号怎样确定?
当负因数有奇数个时,积的符号为负;
当负因数有偶数个时,积的符号为正.
积的符号由负因数的个数决定.
只要有一个因数为0,积就为0.
a×b = b×a
(a×b)×c = a×(b×c)
a×(b+c) = a×b+a×c
乘法交换律:
乘法结合律:
乘法分配律:
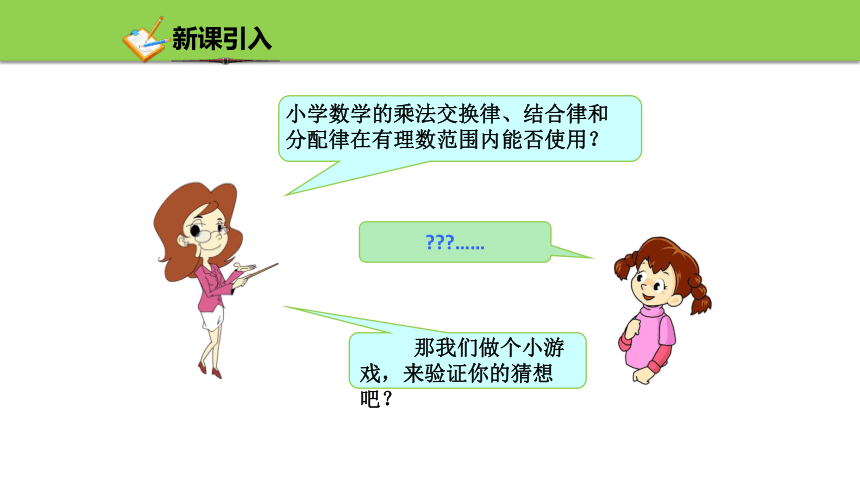
新课引入
在小学我们学过一些乘法的交换律、乘法的结合律以及分配律,你能给大家介绍一下?
……
小学数学的乘法交换律、结合律和分配律在有理数范围内能否使用?
那我们做个小游戏,来验证你的猜想吧?
新课引入
小
游
戏
任选两个有理数(至少有一个为负),分别填入 □和○内,并比较两个结果:
□×○=_________和 ○×□=________
3 ×(-4) = -12
(-4) ×3 = -12
3 ×(-4) = (-4) ×3
比如:
你得到了什么结论?
1
按下列要求探索:
□=3 , ○=-4
新课讲解
小
游
戏
1
在有理数运算中,乘法的交换律依然成立.
两个数相乘,交换因数的位置,积不变.
a×b=b×a
乘法交换律:
新课讲解
小
游
戏
任选三个有理数(至少有一个为负),分别填入□、○和◇中,并比较计算结果:
(□×○)×◇=______
和□×(○×◇)=______
比如:
2
按下列要求探索:
□=3,○= -4,◇=-5
新课讲解
小
游
戏
2
在有理数运算中,乘法的结合律依然成立.
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
(a×b)×c=a×(b×c)
乘法结合律:
新课讲解
任选三个有理数(至少有一个为负),分别填入□、○和◇中,并比较计算结果:
◇×(□+○)=______和◇×□+◇×○=______
小
游
戏
3
按下列要求探索:
比如:
新课讲解
□=3,○= -4,◇=-5
小
游
戏
3
在有理数运算中,乘法的分配律依然成立.
一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
分配律:
a×(b+c)=a×b+a×c
新课讲解
1. 下列各式用了乘法分配律的是( ).
做一做
B
例1 用简便方法计算
例题讲解
(1)
5
6
(-12)×(-37)×-
解:
原式 = +( )
=
=
=
乘法运算时,
第一步做什么?
乘法交换律
乘法结合律
5
6
37×12×-
5
6
37×(12×-)
37×10
370
2. 计算.
做一做
(--)×(- ) ×
2
3
7
5
-
( -- )×
9
14
3
2
(2)
1
2
2
3
4
5
-30×(---+-)
例1 用简便方法计算
例题讲解
解:原式 =
括号内的式子可以看成哪几个数的和?
+
(-30)×
(-30)×
+
(-30)×
=
-15+20-24
= -19
乘法分配律
注意:
1.不要漏掉符号
2.不要漏乘
1
2
-
2
3
(--)
4
5
-
3. 计算.
做一做
(-24)×( - + - )
1
3
3
4
1
6
5
8
例1 用简便方法计算
例题讲解
(3)
4.99×(-12)
解:原式 =
( )×(-12)
= 5 ×(-12)- 0.01×(-12)
乘法分配律
= -60+0.12
=-59.88
5-0.01
4.99与哪个整数比较接近?可以看成哪两个数的和?
4. 计算.
做一做
7-×30
13
15
做一做
5. 下列运算过程有错误的个数是 ( )
①9-×17=(10--)×17=170--;
②-8×(-3)×(-125)=-(8×125×3);
③(63-4-)×3=63-4-×3;
④(-0.25)×(--)×4×(-7)
=-(0.25×4)×(-×7)
A. 1个 B. 2个 C. 3个 D. 4个
32
33
1
33
17
33
1
3
1
3
1
3
1
3
A
解:
60 ×
=60×1-60× -60 × -60 ×
=60-30-15-12
=3
答:够借,还多3个篮球.
(根据什么?)
乘法分配律
例题讲解
1
2
1
4
1
5
(1------)
例2 某校体育器材室共有60个篮球.一天课外活动,有三个班级分别计划借篮球总数的 , 和 .请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,缺几个篮球?
1
2
1
4
1
5
- - -
1
2
-
1
5
-
1
4
-
6. 填空:
绝对值不大于2011的所有整数的
和是________,积是________.
做一做
0
0
小结
a×b=b×a
乘法交换律:
(a×b)×c=a×(b×c)
乘法结合律:
1.乘法运算律
a×(b+c)=a×b+a×c
乘法分配律:
2.利用有理数的乘法运算律进行简便运算.
3.运用有理数的乘法运算律解决实际问题.
随 堂 检 测
思考
如果两个数的乘积为负数,那么这两个数中有几个负数?
如果3个数的乘积为负数,那么这3个数中有几个负数?
4个数呢?
1个
1个或3个
1个或3个或5个
5个数呢?
6个数呢?
你发现了什么规律
1个或3个或5个
1个或3个
合作学习
如果2015个数的乘积为负数,那么这2015个数中,负数的个数有多少种可能?
1个或3个或5个……或2015个.
共1008种可能
根据你得出的规律探索:
如果n个数的乘积为负数,那么这n个数中,负数的个数有多少种可能?
当n为奇数时,
当n为偶数时,
合作学习
共 种可能
n+1
2
共 种可能
n
2
-
再见!
再见!
2.3 有理数的乘法(二)
义务教育课程标准实验教科书
浙教版《数学》七年级上册
教学目标
知识目标
能力目标
情感目标
1.了解乘法交换律、乘法结合律、分配律的意义和运算中的价值.
2.能运用乘法运算律简化乘法运算,解决有关实际问题.
经历探索有理数乘法运算律的过程,进一步提高学生观察、归纳、猜想、验证等能力.
创设合理的问题情景,吸引学生的注意力,激发学生的学习兴趣;在合作学习中,学会交流与合作,培养学生严谨的思维品质.
1.有理数的乘法法则:
任何数与0相乘,积为0.
知识回顾
两数相乘,同号得正,异号得负,并把绝对值相乘.
2.多个不为0的有理数相乘,积的符号怎样确定?
当负因数有奇数个时,积的符号为负;
当负因数有偶数个时,积的符号为正.
积的符号由负因数的个数决定.
只要有一个因数为0,积就为0.
a×b = b×a
(a×b)×c = a×(b×c)
a×(b+c) = a×b+a×c
乘法交换律:
乘法结合律:
乘法分配律:
新课引入
在小学我们学过一些乘法的交换律、乘法的结合律以及分配律,你能给大家介绍一下?
……
小学数学的乘法交换律、结合律和分配律在有理数范围内能否使用?
那我们做个小游戏,来验证你的猜想吧?
新课引入
小
游
戏
任选两个有理数(至少有一个为负),分别填入 □和○内,并比较两个结果:
□×○=_________和 ○×□=________
3 ×(-4) = -12
(-4) ×3 = -12
3 ×(-4) = (-4) ×3
比如:
你得到了什么结论?
1
按下列要求探索:
□=3 , ○=-4
新课讲解
小
游
戏
1
在有理数运算中,乘法的交换律依然成立.
两个数相乘,交换因数的位置,积不变.
a×b=b×a
乘法交换律:
新课讲解
小
游
戏
任选三个有理数(至少有一个为负),分别填入□、○和◇中,并比较计算结果:
(□×○)×◇=______
和□×(○×◇)=______
比如:
2
按下列要求探索:
□=3,○= -4,◇=-5
新课讲解
小
游
戏
2
在有理数运算中,乘法的结合律依然成立.
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
(a×b)×c=a×(b×c)
乘法结合律:
新课讲解
任选三个有理数(至少有一个为负),分别填入□、○和◇中,并比较计算结果:
◇×(□+○)=______和◇×□+◇×○=______
小
游
戏
3
按下列要求探索:
比如:
新课讲解
□=3,○= -4,◇=-5
小
游
戏
3
在有理数运算中,乘法的分配律依然成立.
一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
分配律:
a×(b+c)=a×b+a×c
新课讲解
1. 下列各式用了乘法分配律的是( ).
做一做
B
例1 用简便方法计算
例题讲解
(1)
5
6
(-12)×(-37)×-
解:
原式 = +( )
=
=
=
乘法运算时,
第一步做什么?
乘法交换律
乘法结合律
5
6
37×12×-
5
6
37×(12×-)
37×10
370
2. 计算.
做一做
(--)×(- ) ×
2
3
7
5
-
( -- )×
9
14
3
2
(2)
1
2
2
3
4
5
-30×(---+-)
例1 用简便方法计算
例题讲解
解:原式 =
括号内的式子可以看成哪几个数的和?
+
(-30)×
(-30)×
+
(-30)×
=
-15+20-24
= -19
乘法分配律
注意:
1.不要漏掉符号
2.不要漏乘
1
2
-
2
3
(--)
4
5
-
3. 计算.
做一做
(-24)×( - + - )
1
3
3
4
1
6
5
8
例1 用简便方法计算
例题讲解
(3)
4.99×(-12)
解:原式 =
( )×(-12)
= 5 ×(-12)- 0.01×(-12)
乘法分配律
= -60+0.12
=-59.88
5-0.01
4.99与哪个整数比较接近?可以看成哪两个数的和?
4. 计算.
做一做
7-×30
13
15
做一做
5. 下列运算过程有错误的个数是 ( )
①9-×17=(10--)×17=170--;
②-8×(-3)×(-125)=-(8×125×3);
③(63-4-)×3=63-4-×3;
④(-0.25)×(--)×4×(-7)
=-(0.25×4)×(-×7)
A. 1个 B. 2个 C. 3个 D. 4个
32
33
1
33
17
33
1
3
1
3
1
3
1
3
A
解:
60 ×
=60×1-60× -60 × -60 ×
=60-30-15-12
=3
答:够借,还多3个篮球.
(根据什么?)
乘法分配律
例题讲解
1
2
1
4
1
5
(1------)
例2 某校体育器材室共有60个篮球.一天课外活动,有三个班级分别计划借篮球总数的 , 和 .请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,缺几个篮球?
1
2
1
4
1
5
- - -
1
2
-
1
5
-
1
4
-
6. 填空:
绝对值不大于2011的所有整数的
和是________,积是________.
做一做
0
0
小结
a×b=b×a
乘法交换律:
(a×b)×c=a×(b×c)
乘法结合律:
1.乘法运算律
a×(b+c)=a×b+a×c
乘法分配律:
2.利用有理数的乘法运算律进行简便运算.
3.运用有理数的乘法运算律解决实际问题.
随 堂 检 测
思考
如果两个数的乘积为负数,那么这两个数中有几个负数?
如果3个数的乘积为负数,那么这3个数中有几个负数?
4个数呢?
1个
1个或3个
1个或3个或5个
5个数呢?
6个数呢?
你发现了什么规律
1个或3个或5个
1个或3个
合作学习
如果2015个数的乘积为负数,那么这2015个数中,负数的个数有多少种可能?
1个或3个或5个……或2015个.
共1008种可能
根据你得出的规律探索:
如果n个数的乘积为负数,那么这n个数中,负数的个数有多少种可能?
当n为奇数时,
当n为偶数时,
合作学习
共 种可能
n+1
2
共 种可能
n
2
-
再见!
再见!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
