1.2二次函数的图象 第二课时 课件(共14张PPT)浙教版数学九年级上
文档属性
| 名称 | 1.2二次函数的图象 第二课时 课件(共14张PPT)浙教版数学九年级上 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
1.2二次函数的图象
(2)
义务教育课程标准实验教科书
浙教版《数学》九年级上册
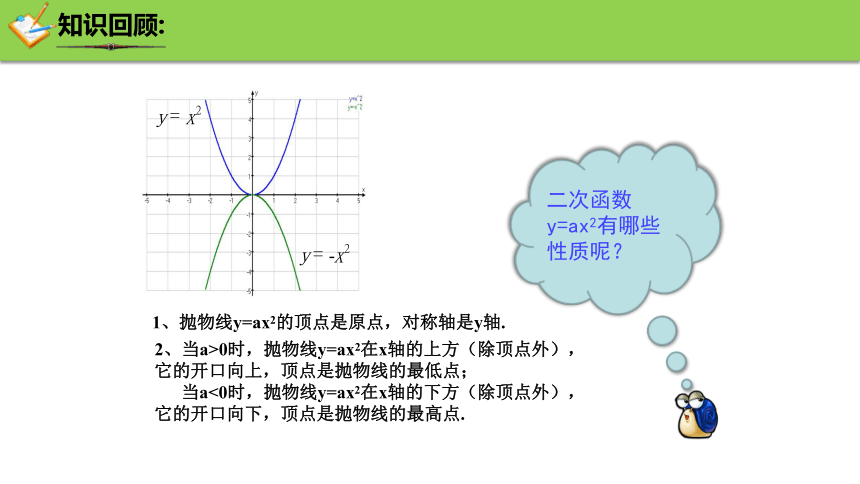
知识回顾:
1、抛物线y=ax2的顶点是原点,对称轴是y轴.
2、当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
二次函数y=ax2有哪些性质呢?
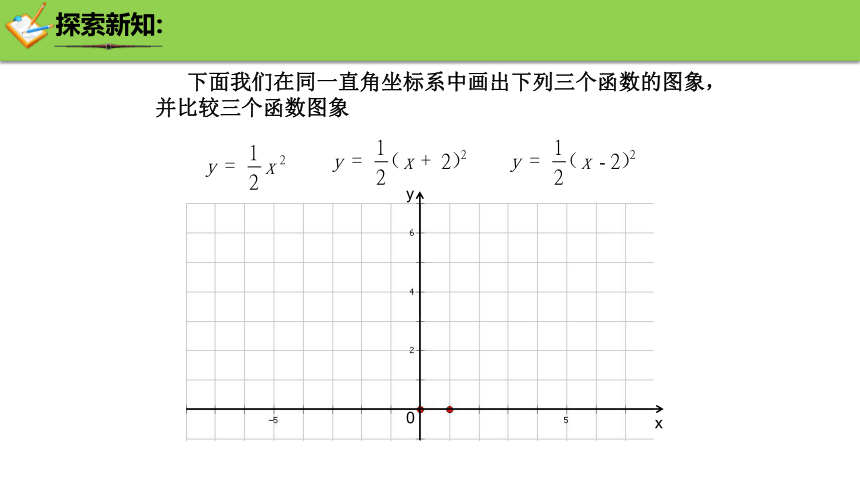
下面我们在同一直角坐标系中画出下列三个函数的图象,并比较三个函数图象
探索新知:
0
x
y
0
x
y
3.函数y=a(x-m)2的顶点坐标是(m,0),对称轴是直线x=m.
讲解新知:
X=-2
X=2
1.函数y=a(x-m)2(a≠0)的图象与函数y=ax2的图象只是位置不同;
2.它由y=ax2的图象向左(当m<0时)或向右(当m>0时)平移|m|个单位得到;
|-2|
|2|
(-2,0)
(2,0)
·
·
X=0
·
(0,0)
x
0
y
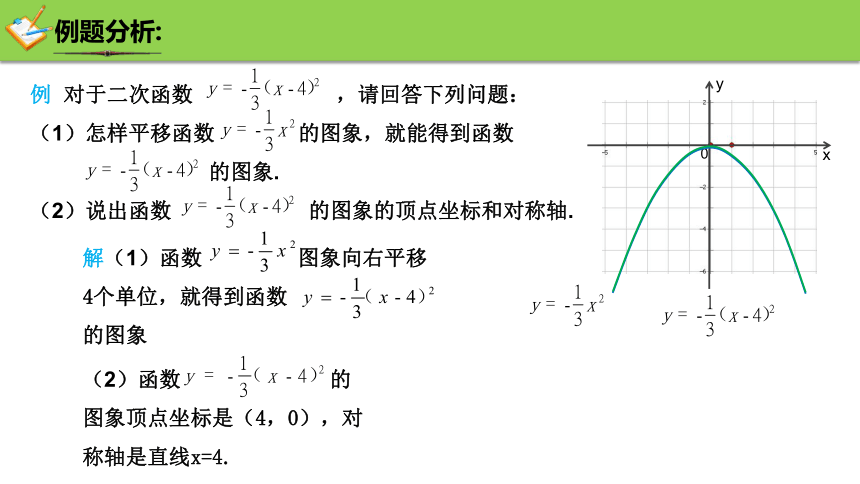
例题分析:
例 对于二次函数 ,请回答下列问题:
(1)怎样平移函数 的图象,就能得到函数
的图象.
(2)说出函数 的图象的顶点坐标和对称轴.
解(1)函数 图象向右平移4个单位,就得到函数 的图象
(2)函数 的图象顶点坐标是(4,0),对称轴是直线x=4.
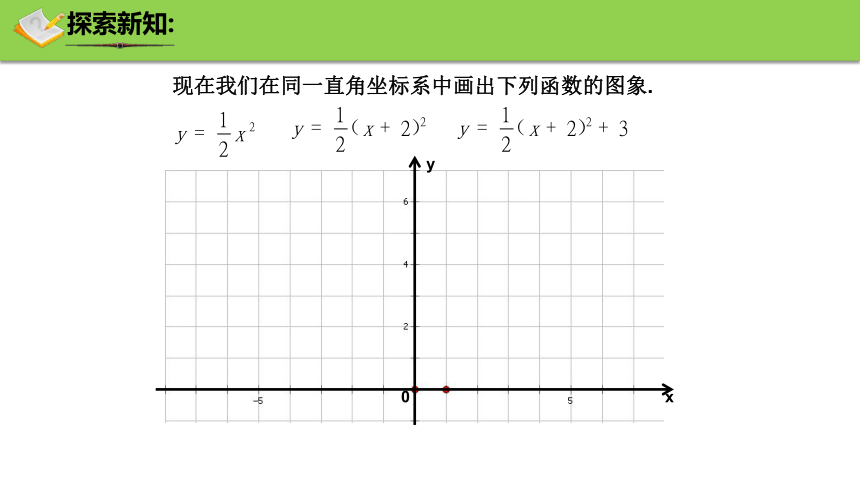
现在我们在同一直角坐标系中画出下列函数的图象.
x
y
0
探索新知:
x
0
y
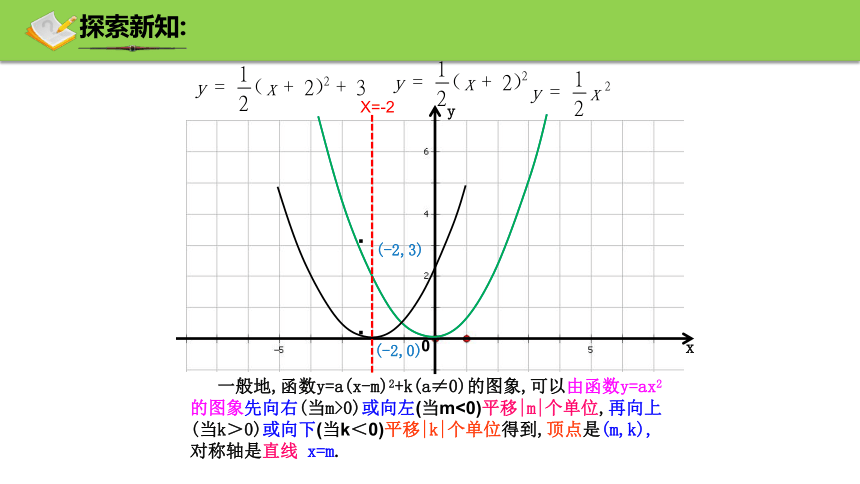
一般地,函数y=a(x-m)2+k(a≠0)的图象,可以由函数y=ax2的图象先向右(当m>0)或向左(当m<0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位得到,顶点是(m,k),对称轴是直线 x=m.
·
(-2,0)
·
(-2,3)
X=-2
探索新知:
填写下表:
二次函数 图象的对称轴 图象的顶点坐标
x=-2
x=-2
x=0,即y轴
(0,0)
(-2,0)
(-2,3)
做一做
练一练
1.填空:
(1)函数y=2(x+1) 2的图象,可以由抛物线________向________平移1个单位得到.
(2)函数y=- (x-7) 2的图象,可以由抛物线________向_______平移1个单位得到.
(3)函数y=3 (x-2) 2+ 的图象,可以由抛物线________向右平移2个单位,再向________平移 个单位得到.
2.说出下列函数图象的开口方向、对称轴和顶点坐标.
(1)
(2)
(3)
(4)
拓展提高
1.如果抛物线 的顶点坐标是(-1,5)
则 ____, ____,
它的对称轴是____________
2.如果一条抛物线的形状与 的形状相同,且顶点坐标是(4,-2),求函数关系式.
1
5
直线x=1
3、已知二次函数 的图象如图所示,
则函数
的图象只可能是( )
D
拓展提高
拓展提高
4.如图,将抛物线 向右平移1个单位得到抛物线 ,回答下列问题:
(1)求抛物线的顶点坐标.
(2)求阴影部分的面积S.
x
0
y
小结
1. 函数y=a(x-m)2(a≠0)的图象与函数y=ax2的图象形状大小一样,只是位置不同可由y=ax2的图象向左(当m<0时)或向右(当m>0时)平移|m|个单位得到,函数y=a(x-m)2的顶点坐标是(m,0),对称轴是直线x=m.
2. 函数y=a(x-m)2+k(a≠0)的图象,可以由函数y=ax2的图象先向右(当m>0)或向左(当m<0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位得到,顶点是(m,k),对称轴是直线 x=m.
再见!
再见!
1.2二次函数的图象
(2)
义务教育课程标准实验教科书
浙教版《数学》九年级上册
知识回顾:
1、抛物线y=ax2的顶点是原点,对称轴是y轴.
2、当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
二次函数y=ax2有哪些性质呢?
下面我们在同一直角坐标系中画出下列三个函数的图象,并比较三个函数图象
探索新知:
0
x
y
0
x
y
3.函数y=a(x-m)2的顶点坐标是(m,0),对称轴是直线x=m.
讲解新知:
X=-2
X=2
1.函数y=a(x-m)2(a≠0)的图象与函数y=ax2的图象只是位置不同;
2.它由y=ax2的图象向左(当m<0时)或向右(当m>0时)平移|m|个单位得到;
|-2|
|2|
(-2,0)
(2,0)
·
·
X=0
·
(0,0)
x
0
y
例题分析:
例 对于二次函数 ,请回答下列问题:
(1)怎样平移函数 的图象,就能得到函数
的图象.
(2)说出函数 的图象的顶点坐标和对称轴.
解(1)函数 图象向右平移4个单位,就得到函数 的图象
(2)函数 的图象顶点坐标是(4,0),对称轴是直线x=4.
现在我们在同一直角坐标系中画出下列函数的图象.
x
y
0
探索新知:
x
0
y
一般地,函数y=a(x-m)2+k(a≠0)的图象,可以由函数y=ax2的图象先向右(当m>0)或向左(当m<0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位得到,顶点是(m,k),对称轴是直线 x=m.
·
(-2,0)
·
(-2,3)
X=-2
探索新知:
填写下表:
二次函数 图象的对称轴 图象的顶点坐标
x=-2
x=-2
x=0,即y轴
(0,0)
(-2,0)
(-2,3)
做一做
练一练
1.填空:
(1)函数y=2(x+1) 2的图象,可以由抛物线________向________平移1个单位得到.
(2)函数y=- (x-7) 2的图象,可以由抛物线________向_______平移1个单位得到.
(3)函数y=3 (x-2) 2+ 的图象,可以由抛物线________向右平移2个单位,再向________平移 个单位得到.
2.说出下列函数图象的开口方向、对称轴和顶点坐标.
(1)
(2)
(3)
(4)
拓展提高
1.如果抛物线 的顶点坐标是(-1,5)
则 ____, ____,
它的对称轴是____________
2.如果一条抛物线的形状与 的形状相同,且顶点坐标是(4,-2),求函数关系式.
1
5
直线x=1
3、已知二次函数 的图象如图所示,
则函数
的图象只可能是( )
D
拓展提高
拓展提高
4.如图,将抛物线 向右平移1个单位得到抛物线 ,回答下列问题:
(1)求抛物线的顶点坐标.
(2)求阴影部分的面积S.
x
0
y
小结
1. 函数y=a(x-m)2(a≠0)的图象与函数y=ax2的图象形状大小一样,只是位置不同可由y=ax2的图象向左(当m<0时)或向右(当m>0时)平移|m|个单位得到,函数y=a(x-m)2的顶点坐标是(m,0),对称轴是直线x=m.
2. 函数y=a(x-m)2+k(a≠0)的图象,可以由函数y=ax2的图象先向右(当m>0)或向左(当m<0)平移|m|个单位,再向上(当k>0)或向下(当k<0)平移|k|个单位得到,顶点是(m,k),对称轴是直线 x=m.
再见!
再见!
同课章节目录
