1.3二次函数的性质 课件(共18张PPT)浙教版数学九年级上
文档属性
| 名称 | 1.3二次函数的性质 课件(共18张PPT)浙教版数学九年级上 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 10:45:37 | ||
图片预览


文档简介
(共18张PPT)
1.3二次函数的性质
义务教育课程标准实验教科书
浙教版《数学》九年级上册
导入新课
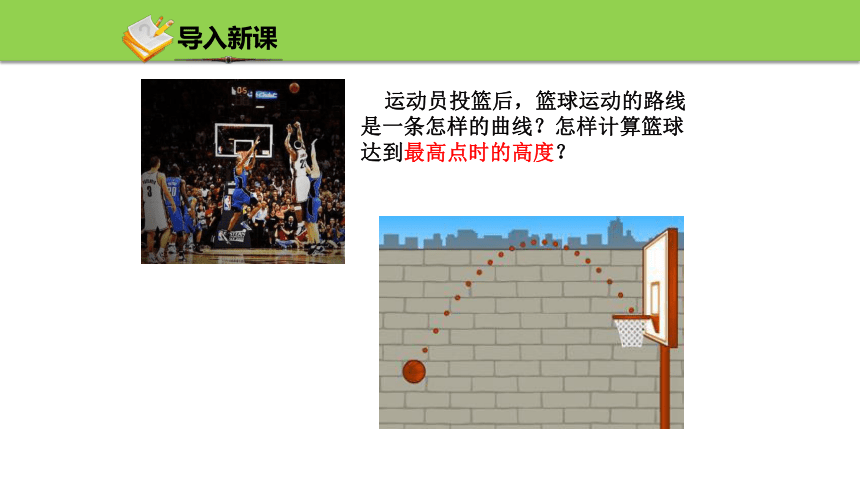
运动员投篮后,篮球运动的路线是一条怎样的曲线?怎样计算篮球达到最高点时的高度?
探索新知
0
x
y
y=2x +4x-6
y= x -3x
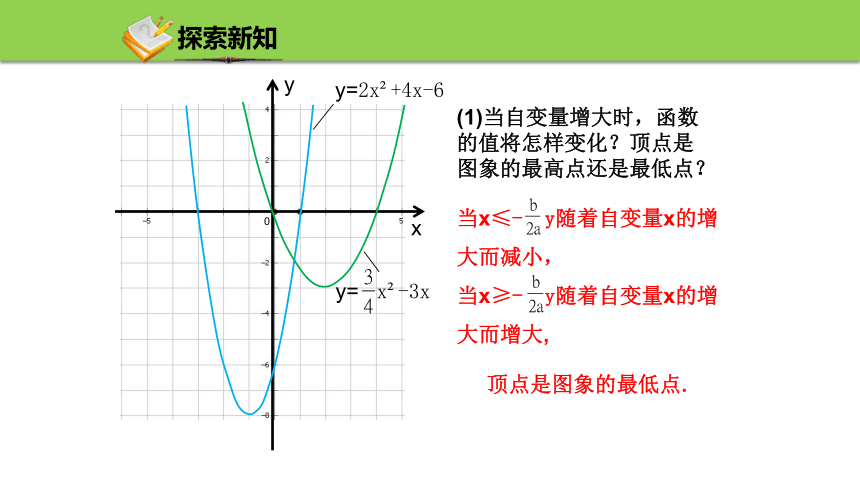
(1)当自变量增大时,函数的值将怎样变化?顶点是图象的最高点还是最低点?
当x≤- y随着自变量x的增大而减小,
当x≥- y随着自变量x的增大而增大,
顶点是图象的最低点.
0
x
y
探索新知
y=- x +2x-
y=- x + x-6
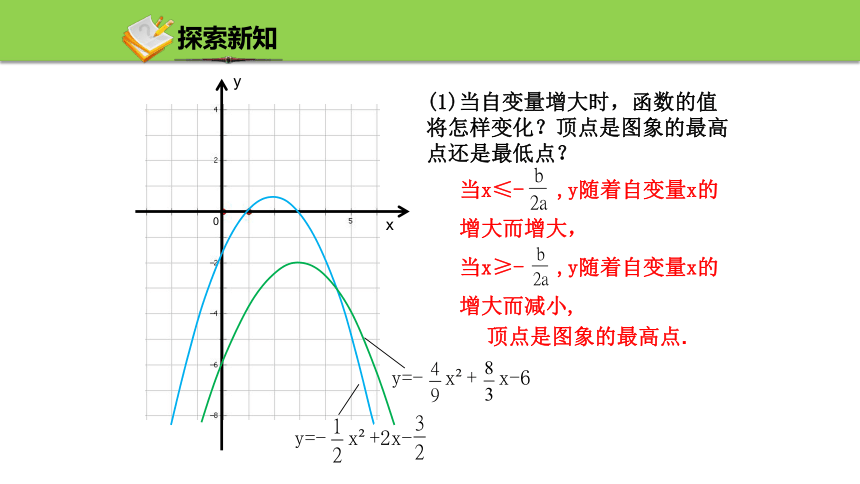
(1)当自变量增大时,函数的值将怎样变化?顶点是图象的最高点还是最低点?
当x≤- ,y随着自变量x的增大而增大,
当x≥- ,y随着自变量x的增大而减小,
顶点是图象的最高点.
0
x
y
y=2x +4x-6
y= x -3x
0
x
y
y=- x +2x-
y=- x + x-6
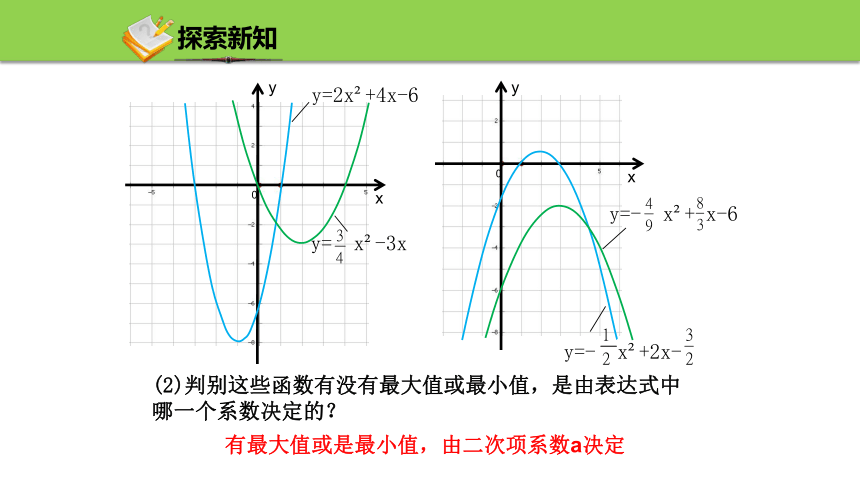
(2)判别这些函数有没有最大值或最小值,是由表达式中哪一个系数决定的?
有最大值或是最小值,由二次项系数a决定
探索新知
y
x
0
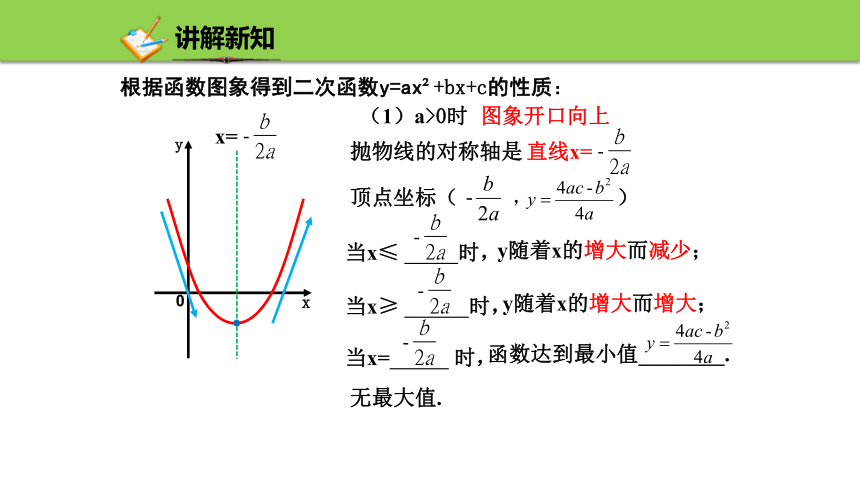
根据函数图象得到二次函数y=ax +bx+c的性质:
(1)a>0时
图象开口向上
抛物线的对称轴是
直线x=
当x≤ 时,
y随着x的增大而减少;
当x≥ 时,
y随着x的增大而增大;
当x= 时,
函数达到最小值________.
无最大值.
讲解新知
顶点坐标( , )
x=
0
y
x
(2)a<0时
图象开口向下
抛物线的对称轴是
直线x=
当x≤ 时,
y随着x的增大而增大;
当x≥ 时,
y随着x的增大而减小;
当x= 时,
函数达到最大值________.
无最小值.
讲解新知
顶点坐标( , )
根据函数图象得到二次函数y=ax +bx+c的性质:
y
x
0
y
x
0
y
x
0
讲解新知
图象与坐标轴的交点
① b -4ac>0
② b -4ac=0
③ b -4ac<0
(a>0)
求交点:
与x轴交点,令y=0 得 ax +bx+c=0
与y轴交点,令x=0 得 y=c
二次函数y=ax2+bx+c的图象
和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的个数由什么决定的?
讲解新知
图象与坐标轴的交点
b -4ac>0
b -4ac=0
b -4ac<0
(a<0)
0
y
x
0
y
x
0
y
x
求交点:
与x轴交点,令y=0 得 ax +bx+c=0
与y轴交点,令x=0 得 y=c
二次函数y=ax2+bx+c的图象
和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
例题分析:
例 已知函数
(1) 求函数图象的顶点坐标、对称轴,以及图象与坐标轴的交点坐标,并画出函数的大致图象.
解 (1)∵a=- ,b=-7,c=
∴
顶点坐标是(-7,32)
由x=0,得y= ,所以图象与y轴的交点是(0, )
对称轴是直线x=-7
由y=0,得 ,
所以图象与x轴的交点是(-15,0 ), (1,0 ).
x
y
0
10
-10
-20
-10
10
20
30
(-7,32)
(-15,0)
(1,0)
(0, )
解得
例题分析:
例 已知函数
(2) 自变量x在什么范围内时,y随x的增大而增大?何时y随x的增大而减小?并求出函数的最大值或最小值.
(2)由图象可知,
当x≤-7时,y随x的增大而增大;
当x≥-7时,y随x的增大而减小;
当x=-7时,函数y有最大值32.
解
x
y
0
10
-10
-20
-10
10
20
30
(-7,32)
(-15,0)
(1,0)
(0, )
想一想:
ax +bx+c=0
y=ax +bx+c
方程
函数
有什么关系?
与
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.
练一练
1.已知函数
(1)求函数图象的顶点坐标、对称轴和与坐标轴交点的坐标,并画出函数的大致图象.
(2)记当 时对应的函数
值分别为
试比较 的大小.
练一练
2.求下列函数的最大值(或最小值)和对应的自变量的值.
1、二次函数y=ax2+bx+c(a≠0)的图象如图所示,
则a、b、c的符号为
y
x
o
2、二次函数y=x2 -4x+3 的对称轴是
3、一抛物线y=-2x2的形状和开口方向相同,顶点为
(1,- 4),则它的函数解析式为
4、抛物线y=x2-5x+4 与坐标轴的交点个数为( )
(A)0个 (B)1个 (C)2个 (D)3个
5、说出下列抛物线与x轴的交点的个数:
⑴ y=2x2-x-1 ⑵ y=4x2+4x+1 ⑶ y=3x2+2x+5
a<0
c>0
b>0
直线x=2
y=-2(x –1)2 -4
C
拓展提高
2个
1个
0个
拓展提高
6.篮球运动员投篮后,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为直线x=2.5.求:
(1)球运动路线的函数表达式和自变量的取值范围.
(2)球在运动中离地面的最大高度.
x
y
0
3.05m
2.25m
4m
小结
一般地,二次函数y=ax +bx+c(a≠0)有以下性质:
条件
图象
增减性
最大(小)值
a>0
a<0
b -4ac>0
b -4ac=0
b -4ac<0
x
0
y
当x≥ 时,
当x≤ 时,
y随着x的增大而减少;
y随着x的增大而增大;
当x≥ 时,
当x≤ 时,
y随着x的增大而增大;
y随着x的增大而减小;
当x= 时,
y达到最小值:
无最大值.
当x= 时,
y达到最大值:
无最小值.
0
y
x
0
y
x
0
y
x
x
0
y
x
0
y
再见!
再见!
1.3二次函数的性质
义务教育课程标准实验教科书
浙教版《数学》九年级上册
导入新课
运动员投篮后,篮球运动的路线是一条怎样的曲线?怎样计算篮球达到最高点时的高度?
探索新知
0
x
y
y=2x +4x-6
y= x -3x
(1)当自变量增大时,函数的值将怎样变化?顶点是图象的最高点还是最低点?
当x≤- y随着自变量x的增大而减小,
当x≥- y随着自变量x的增大而增大,
顶点是图象的最低点.
0
x
y
探索新知
y=- x +2x-
y=- x + x-6
(1)当自变量增大时,函数的值将怎样变化?顶点是图象的最高点还是最低点?
当x≤- ,y随着自变量x的增大而增大,
当x≥- ,y随着自变量x的增大而减小,
顶点是图象的最高点.
0
x
y
y=2x +4x-6
y= x -3x
0
x
y
y=- x +2x-
y=- x + x-6
(2)判别这些函数有没有最大值或最小值,是由表达式中哪一个系数决定的?
有最大值或是最小值,由二次项系数a决定
探索新知
y
x
0
根据函数图象得到二次函数y=ax +bx+c的性质:
(1)a>0时
图象开口向上
抛物线的对称轴是
直线x=
当x≤ 时,
y随着x的增大而减少;
当x≥ 时,
y随着x的增大而增大;
当x= 时,
函数达到最小值________.
无最大值.
讲解新知
顶点坐标( , )
x=
0
y
x
(2)a<0时
图象开口向下
抛物线的对称轴是
直线x=
当x≤ 时,
y随着x的增大而增大;
当x≥ 时,
y随着x的增大而减小;
当x= 时,
函数达到最大值________.
无最小值.
讲解新知
顶点坐标( , )
根据函数图象得到二次函数y=ax +bx+c的性质:
y
x
0
y
x
0
y
x
0
讲解新知
图象与坐标轴的交点
① b -4ac>0
② b -4ac=0
③ b -4ac<0
(a>0)
求交点:
与x轴交点,令y=0 得 ax +bx+c=0
与y轴交点,令x=0 得 y=c
二次函数y=ax2+bx+c的图象
和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的个数由什么决定的?
讲解新知
图象与坐标轴的交点
b -4ac>0
b -4ac=0
b -4ac<0
(a<0)
0
y
x
0
y
x
0
y
x
求交点:
与x轴交点,令y=0 得 ax +bx+c=0
与y轴交点,令x=0 得 y=c
二次函数y=ax2+bx+c的图象
和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
例题分析:
例 已知函数
(1) 求函数图象的顶点坐标、对称轴,以及图象与坐标轴的交点坐标,并画出函数的大致图象.
解 (1)∵a=- ,b=-7,c=
∴
顶点坐标是(-7,32)
由x=0,得y= ,所以图象与y轴的交点是(0, )
对称轴是直线x=-7
由y=0,得 ,
所以图象与x轴的交点是(-15,0 ), (1,0 ).
x
y
0
10
-10
-20
-10
10
20
30
(-7,32)
(-15,0)
(1,0)
(0, )
解得
例题分析:
例 已知函数
(2) 自变量x在什么范围内时,y随x的增大而增大?何时y随x的增大而减小?并求出函数的最大值或最小值.
(2)由图象可知,
当x≤-7时,y随x的增大而增大;
当x≥-7时,y随x的增大而减小;
当x=-7时,函数y有最大值32.
解
x
y
0
10
-10
-20
-10
10
20
30
(-7,32)
(-15,0)
(1,0)
(0, )
想一想:
ax +bx+c=0
y=ax +bx+c
方程
函数
有什么关系?
与
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.
练一练
1.已知函数
(1)求函数图象的顶点坐标、对称轴和与坐标轴交点的坐标,并画出函数的大致图象.
(2)记当 时对应的函数
值分别为
试比较 的大小.
练一练
2.求下列函数的最大值(或最小值)和对应的自变量的值.
1、二次函数y=ax2+bx+c(a≠0)的图象如图所示,
则a、b、c的符号为
y
x
o
2、二次函数y=x2 -4x+3 的对称轴是
3、一抛物线y=-2x2的形状和开口方向相同,顶点为
(1,- 4),则它的函数解析式为
4、抛物线y=x2-5x+4 与坐标轴的交点个数为( )
(A)0个 (B)1个 (C)2个 (D)3个
5、说出下列抛物线与x轴的交点的个数:
⑴ y=2x2-x-1 ⑵ y=4x2+4x+1 ⑶ y=3x2+2x+5
a<0
c>0
b>0
直线x=2
y=-2(x –1)2 -4
C
拓展提高
2个
1个
0个
拓展提高
6.篮球运动员投篮后,球运动的路线为抛物线的一部分(如图),抛物线的对称轴为直线x=2.5.求:
(1)球运动路线的函数表达式和自变量的取值范围.
(2)球在运动中离地面的最大高度.
x
y
0
3.05m
2.25m
4m
小结
一般地,二次函数y=ax +bx+c(a≠0)有以下性质:
条件
图象
增减性
最大(小)值
a>0
a<0
b -4ac>0
b -4ac=0
b -4ac<0
x
0
y
当x≥ 时,
当x≤ 时,
y随着x的增大而减少;
y随着x的增大而增大;
当x≥ 时,
当x≤ 时,
y随着x的增大而增大;
y随着x的增大而减小;
当x= 时,
y达到最小值:
无最大值.
当x= 时,
y达到最大值:
无最小值.
0
y
x
0
y
x
0
y
x
x
0
y
x
0
y
再见!
再见!
同课章节目录
