1.2二次函数的图象 第一课时 课件(共12张PPT)浙教版数学九年级上
文档属性
| 名称 | 1.2二次函数的图象 第一课时 课件(共12张PPT)浙教版数学九年级上 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览


文档简介
(共12张PPT)
1.2二次函数的图像(1)
义务教育课程标准实验教科书
浙教版《数学》九年级上册
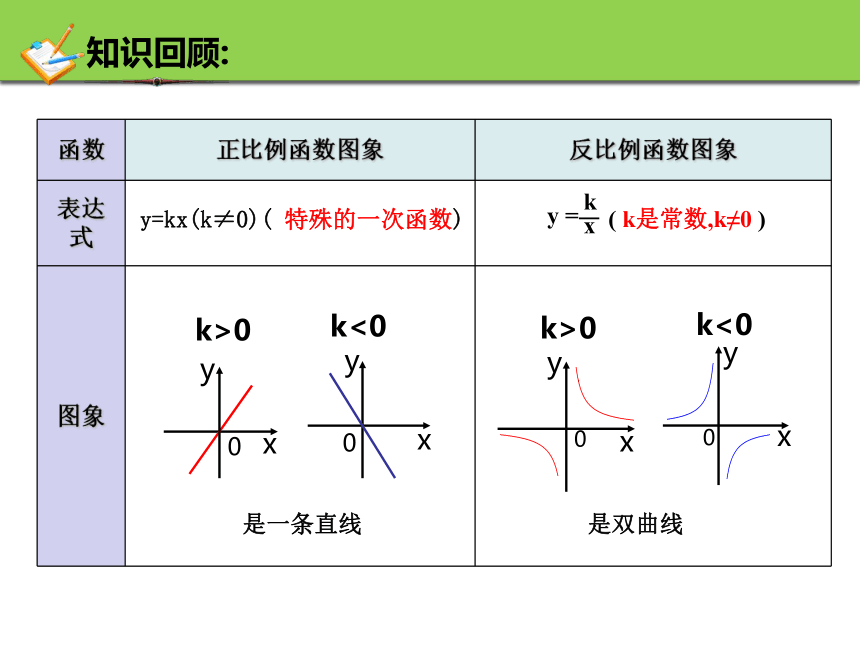
函数 正比例函数图象 反比例函数图象
表达式
图象
y=kx(k≠0)( 特殊的一次函数)
k<0
x
y
0
x
y
0
k>0
k<0
y
x
0
y
0
k>0
x
( k是常数,k≠0 )
y =
x
k
知识回顾:
是一条直线
是双曲线
新课导入:
二次函数的图象又是怎样的呢?
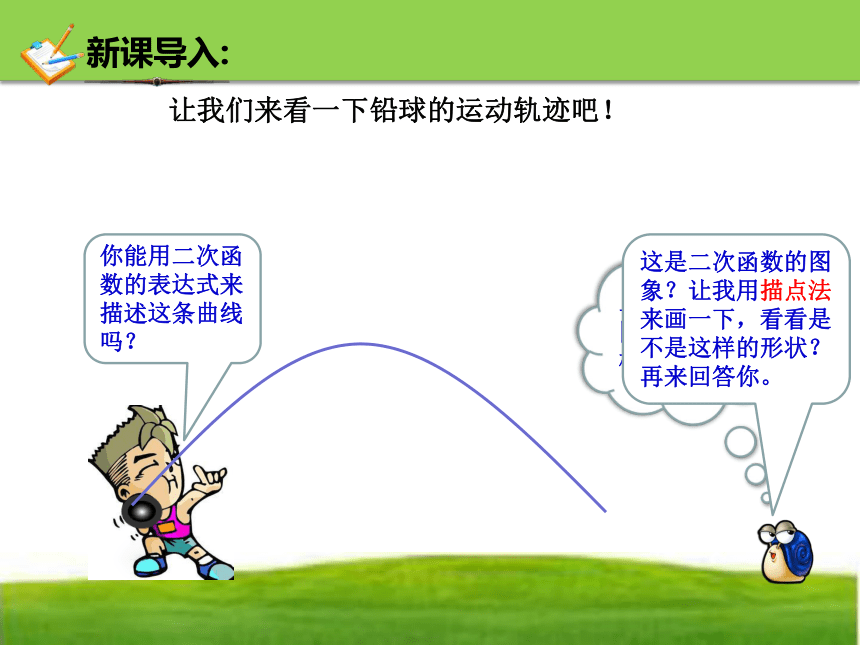
让我们来看一下铅球的运动轨迹吧!
你能用二次函数的表达式来描述这条曲线吗?
这是二次函数的图象?让我用描点法来画一下,看看是不是这样的形状?
再来回答你。
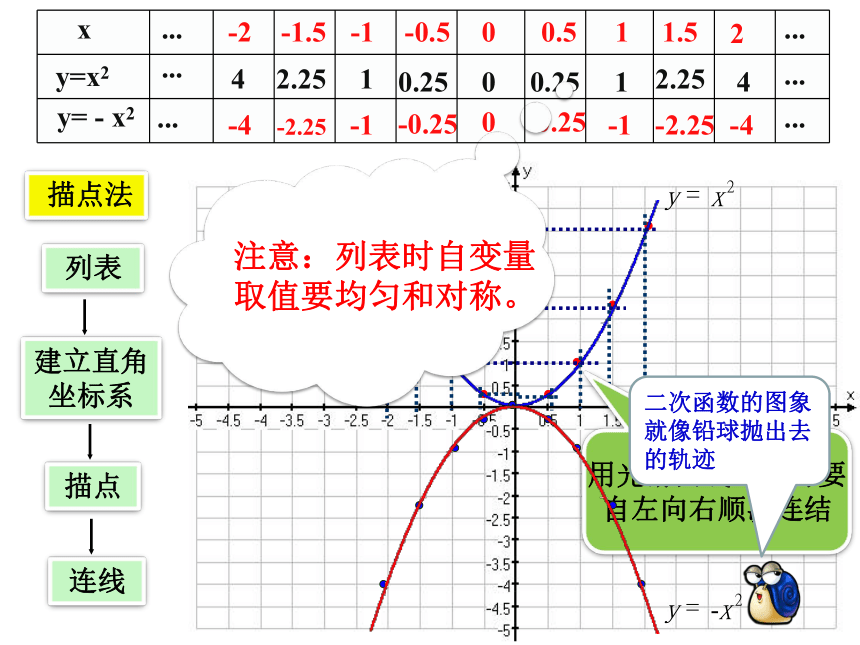
x
y=x2
y= - x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
0
0.25
1
2.25
4
0.25
1
2.25
4
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
二次函数的图象就像铅球抛出去的轨迹
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线.
抛物线关于y轴
对称,y轴就是它的
对称轴.
对称轴与抛物线的交点
叫做抛物线的顶点.
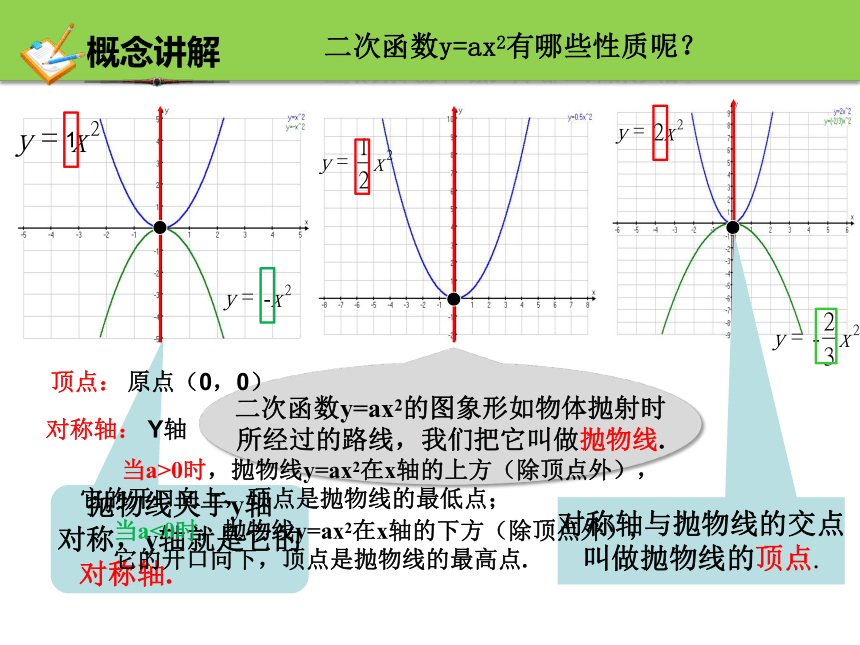
概念讲解
顶点:
对称轴:
原点(0,0)
Y轴
当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
1
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
1.在同一坐标系中画出下列二次函数的图象.
(2,2)
(-2,2)
(2,-2)
(-2,-2)
x
y
0
做一做
例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3). (1)求a的值,并写出这个二次函数的表达式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图象的位置.
例题分析
我会解决这个问题了!
x
y
0
m
n
设y=ax
(m,n)
把x=m,y=n代入y=ax ,
n=am ,解得a=
∴y= x
你太捧了!
例题分析
练一练
1.若抛物线y=ax2 (a ≠ 0),过点(-1,3),则
a的值是 ,对称轴是 ,开口 .
顶点坐标是 ,顶点是抛物线上的 .
抛物线在x轴的 方(除顶点外).
一展身手
1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数表达式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解:(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,
解出a= -2,所求函数表达式为y= -2x2.
(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上.
(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
小结
二次函数的图象:
二次函数的性质:
二次函数y=ax2的图象是一条抛物线.
1、抛物线y=ax2的顶点是原点,对称轴是y轴。
2、当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
再见!
再见!
1.2二次函数的图像(1)
义务教育课程标准实验教科书
浙教版《数学》九年级上册
函数 正比例函数图象 反比例函数图象
表达式
图象
y=kx(k≠0)( 特殊的一次函数)
k<0
x
y
0
x
y
0
k>0
k<0
y
x
0
y
0
k>0
x
( k是常数,k≠0 )
y =
x
k
知识回顾:
是一条直线
是双曲线
新课导入:
二次函数的图象又是怎样的呢?
让我们来看一下铅球的运动轨迹吧!
你能用二次函数的表达式来描述这条曲线吗?
这是二次函数的图象?让我用描点法来画一下,看看是不是这样的形状?
再来回答你。
x
y=x2
y= - x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
0
0.25
1
2.25
4
0.25
1
2.25
4
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
二次函数的图象就像铅球抛出去的轨迹
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线.
抛物线关于y轴
对称,y轴就是它的
对称轴.
对称轴与抛物线的交点
叫做抛物线的顶点.
概念讲解
顶点:
对称轴:
原点(0,0)
Y轴
当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
1
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
1.在同一坐标系中画出下列二次函数的图象.
(2,2)
(-2,2)
(2,-2)
(-2,-2)
x
y
0
做一做
例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3). (1)求a的值,并写出这个二次函数的表达式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图象的位置.
例题分析
我会解决这个问题了!
x
y
0
m
n
设y=ax
(m,n)
把x=m,y=n代入y=ax ,
n=am ,解得a=
∴y= x
你太捧了!
例题分析
练一练
1.若抛物线y=ax2 (a ≠ 0),过点(-1,3),则
a的值是 ,对称轴是 ,开口 .
顶点坐标是 ,顶点是抛物线上的 .
抛物线在x轴的 方(除顶点外).
一展身手
1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数表达式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解:(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,
解出a= -2,所求函数表达式为y= -2x2.
(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上.
(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
小结
二次函数的图象:
二次函数的性质:
二次函数y=ax2的图象是一条抛物线.
1、抛物线y=ax2的顶点是原点,对称轴是y轴。
2、当a>0时,抛物线y=ax2在x轴的上方(除顶点外),
它的开口向上,顶点是抛物线的最低点;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),
它的开口向下,顶点是抛物线的最高点.
再见!
再见!
同课章节目录
