2.6直角三角形(1)课件(共20张PPT) 2023—2024学年浙教版数学八年级上册
文档属性
| 名称 | 2.6直角三角形(1)课件(共20张PPT) 2023—2024学年浙教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 10:39:40 | ||
图片预览




文档简介
(共20张PPT)
2.6直角三角形 (1)
浙教版 八年级上
1.认识直角三角形
2.掌握直角三角形的两个锐角互余的性质定理
3.掌握“直角三角形斜边上的中线等于斜边的一半”的性质!
学习目标
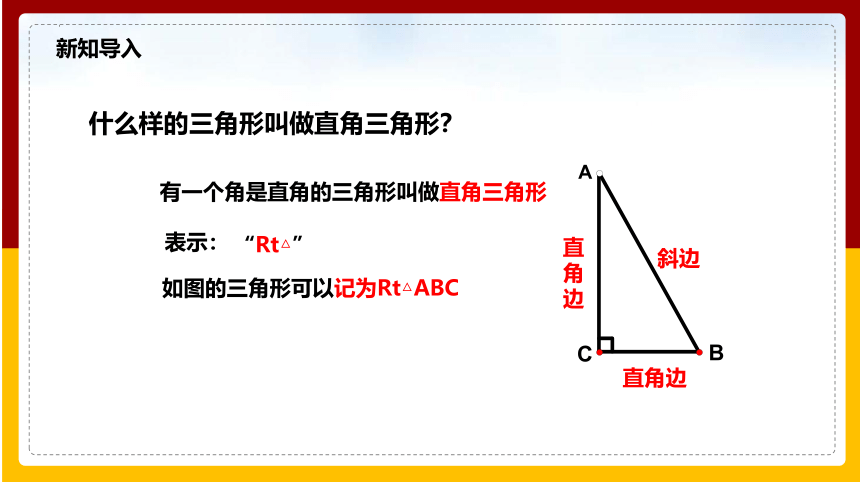
新知导入
什么样的三角形叫做直角三角形?
有一个角是直角的三角形叫做直角三角形
表示:
“Rt△”
如图的三角形可以记为Rt△ABC
斜边
直
角
边
直角边
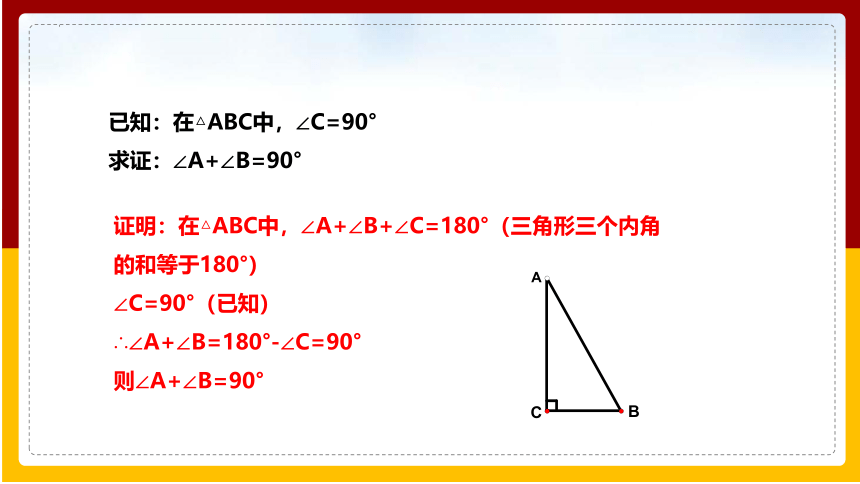
已知:在△ABC中,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°)
∠C=90°(已知)
∴∠A+∠B=180°-∠C=90°
则∠A+∠B=90°
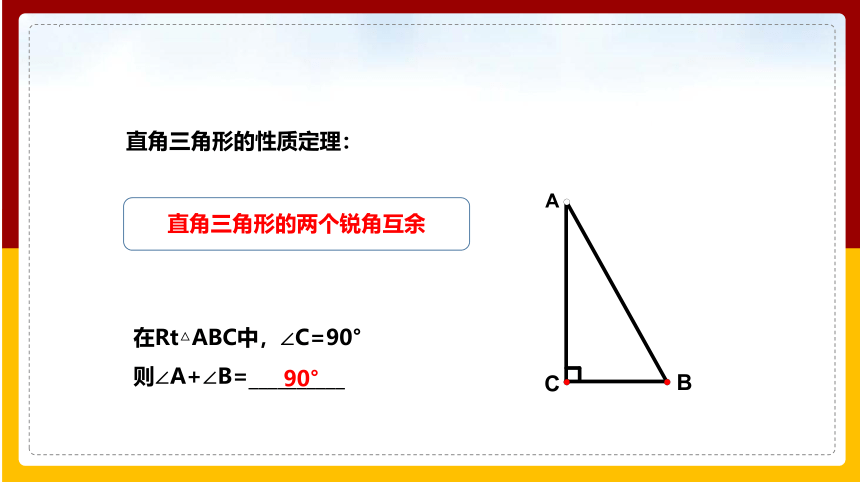
直角三角形的两个锐角互余
直角三角形的性质定理:
在Rt△ABC中,∠C=90°
则∠A+∠B=__________
90°
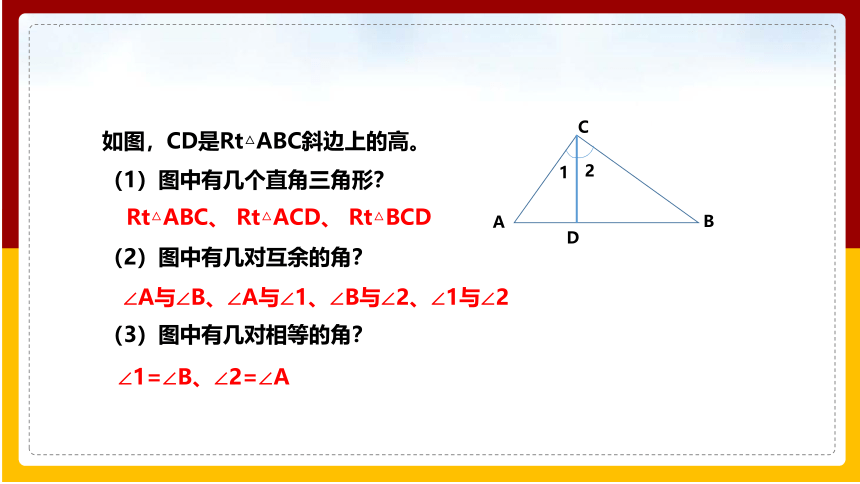
如图,CD是Rt△ABC斜边上的高。
(1)图中有几个直角三角形?
(2)图中有几对互余的角?
(3)图中有几对相等的角?
Rt△ABC、 Rt△ACD、 Rt△BCD
∠A与∠B、∠A与∠1、∠B与∠2、∠1与∠2
∠1=∠B、∠2=∠A
C
A
D
B
1
2
已知直角三角形两个锐角的度数之比为3:2,求这两个锐角的度数.
解:设这两个锐角的度数为3x,2x
则3x+2x=90°
解得x=18°
∴这两个锐角的度数为54°,36°。
【做一做】
任意画一个直角三角形,作出斜边上的中线,并利用圆规比较中线与斜边的一半的长短,你发现了什么?
再画几个直角三角形试一试,你的发现相同吗?
猜想:直角三角形斜边上的中线等于斜边的一半.
B
A
C
D
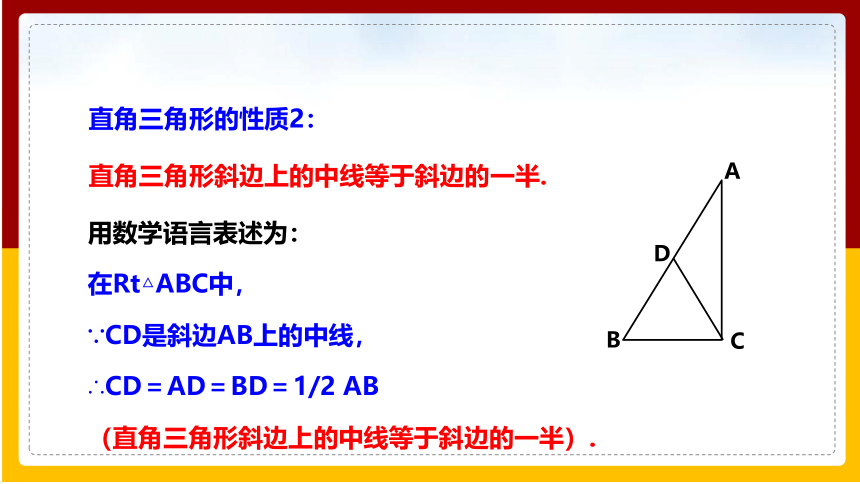
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半.
用数学语言表述为:
在Rt△ABC中,
∵CD是斜边AB上的中线,
∴CD=AD=BD=1/2 AB
(直角三角形斜边上的中线等于斜边的一半).
B
A
C
D
新知讲解
例1 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B.已知AB=200m,问这名滑雪运动员的高度下降了多少米?
解:如图,作Rt△ABC的斜边上的中线CD,
则CD=AD=0.5AB=0.5×200=100(m)(直角三角形斜边上的中线等于斜边的一半).
∵∠B=30 ,
∴∠A=90 -∠B=90 -30 =60
(直角三角形的两个锐角互余) .
A
B
C
D
∴△ADC是等边三角形
(有一个角是60°的等腰三角形是等边三角形).
∴ AC=AD=100(m).
答:这名滑雪运动员的高度下降了100m.
A
B
C
D
从例1的结果,你能得到什么结论?
在直角三角形中,30°角所对的直角边等于斜边的一半
B
A
C
直角三角形性质定理:
课堂练习
1.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
D
2.如图,在Rt△ACB中,∠ACB=90°,CD为AB边上的中线,
∠A=30°. 若CD=6,则BC的长度为( )
A.2 B.4 C.6 D.8
C
3.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
证明:∵∠ACB=90°,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B.
证明:在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
3.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(2)若AF平分∠CAB分别交CD,BC于E,F,求证:∠CEF=∠CFE.
4.在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,猜一猜MN与BD的位置关系,再证明你的结论.
解:MN与BD的位置关系是MN垂
直且平分BD,
证明:连结BM,DM,如答图,
∵∠ABC=90°,∠ADC=90°,
M为AC中点,
∴BM=DM,
∵N为BD中点,
∴MN⊥BD,BN=DN,
即MN与BD的位置关系是MN垂直且平分BD.
课堂总结
直角三角形的性质:
1、直角三角形的两个锐角互余
2、直角三角形斜边上的中线等于斜边的一半
3、在直角三角形中,30°角所对的直角边等于斜边的一半
4、等腰直角三角形的两个锐角都是45°
本节课你学到了什么?
2.6直角三角形 (1)
浙教版 八年级上
1.认识直角三角形
2.掌握直角三角形的两个锐角互余的性质定理
3.掌握“直角三角形斜边上的中线等于斜边的一半”的性质!
学习目标
新知导入
什么样的三角形叫做直角三角形?
有一个角是直角的三角形叫做直角三角形
表示:
“Rt△”
如图的三角形可以记为Rt△ABC
斜边
直
角
边
直角边
已知:在△ABC中,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°)
∠C=90°(已知)
∴∠A+∠B=180°-∠C=90°
则∠A+∠B=90°
直角三角形的两个锐角互余
直角三角形的性质定理:
在Rt△ABC中,∠C=90°
则∠A+∠B=__________
90°
如图,CD是Rt△ABC斜边上的高。
(1)图中有几个直角三角形?
(2)图中有几对互余的角?
(3)图中有几对相等的角?
Rt△ABC、 Rt△ACD、 Rt△BCD
∠A与∠B、∠A与∠1、∠B与∠2、∠1与∠2
∠1=∠B、∠2=∠A
C
A
D
B
1
2
已知直角三角形两个锐角的度数之比为3:2,求这两个锐角的度数.
解:设这两个锐角的度数为3x,2x
则3x+2x=90°
解得x=18°
∴这两个锐角的度数为54°,36°。
【做一做】
任意画一个直角三角形,作出斜边上的中线,并利用圆规比较中线与斜边的一半的长短,你发现了什么?
再画几个直角三角形试一试,你的发现相同吗?
猜想:直角三角形斜边上的中线等于斜边的一半.
B
A
C
D
直角三角形的性质2:
直角三角形斜边上的中线等于斜边的一半.
用数学语言表述为:
在Rt△ABC中,
∵CD是斜边AB上的中线,
∴CD=AD=BD=1/2 AB
(直角三角形斜边上的中线等于斜边的一半).
B
A
C
D
新知讲解
例1 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B.已知AB=200m,问这名滑雪运动员的高度下降了多少米?
解:如图,作Rt△ABC的斜边上的中线CD,
则CD=AD=0.5AB=0.5×200=100(m)(直角三角形斜边上的中线等于斜边的一半).
∵∠B=30 ,
∴∠A=90 -∠B=90 -30 =60
(直角三角形的两个锐角互余) .
A
B
C
D
∴△ADC是等边三角形
(有一个角是60°的等腰三角形是等边三角形).
∴ AC=AD=100(m).
答:这名滑雪运动员的高度下降了100m.
A
B
C
D
从例1的结果,你能得到什么结论?
在直角三角形中,30°角所对的直角边等于斜边的一半
B
A
C
直角三角形性质定理:
课堂练习
1.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km
C.0.9 km D.1.2 km
D
2.如图,在Rt△ACB中,∠ACB=90°,CD为AB边上的中线,
∠A=30°. 若CD=6,则BC的长度为( )
A.2 B.4 C.6 D.8
C
3.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(1)求证:∠ACD=∠B;
证明:∵∠ACB=90°,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B.
证明:在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,
又∵∠CEF=∠AED,∴∠CEF=∠CFE.
3.如图,在△ACB中,∠ACB=90°,CD⊥AB于D.
(2)若AF平分∠CAB分别交CD,BC于E,F,求证:∠CEF=∠CFE.
4.在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,猜一猜MN与BD的位置关系,再证明你的结论.
解:MN与BD的位置关系是MN垂
直且平分BD,
证明:连结BM,DM,如答图,
∵∠ABC=90°,∠ADC=90°,
M为AC中点,
∴BM=DM,
∵N为BD中点,
∴MN⊥BD,BN=DN,
即MN与BD的位置关系是MN垂直且平分BD.
课堂总结
直角三角形的性质:
1、直角三角形的两个锐角互余
2、直角三角形斜边上的中线等于斜边的一半
3、在直角三角形中,30°角所对的直角边等于斜边的一半
4、等腰直角三角形的两个锐角都是45°
本节课你学到了什么?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
