第4章 图形与坐标 单元精选精练(含解析)
文档属性
| 名称 | 第4章 图形与坐标 单元精选精练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 567.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-09 17:44:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第4章 图形与坐标 单元精选精练 2023-2024学年浙教版八年级数学上册 (含解析)
一、单选题
1.(2023春·湖南株洲·八年级统考期末)小军参加团体操表演,他的位置用数对表示是,如果这时的方队是一个正方形,参加团体操表演的至少有( )人.
A.80 B.64 C.24 D.11
2.(2021春·重庆万州·八年级统考期末)已知点P(m﹣1,4)与点Q(2,n﹣2)关于x轴对称,则mn的值为( )
A.9 B.﹣9 C.﹣ D.
3.(2021秋·福建三明·八年级统考期末)已知点M(3,﹣2),N(3,﹣1),则线段MN与x轴( )
A.垂直 B.平行 C.相交 D.不垂直
4.(2023秋·辽宁锦州·八年级统考期末)如图,若点E的坐标为,点G的坐标为,则点F的坐标为( )
A. B. C. D.
5.(2022秋·浙江温州·八年级统考期末)下列选项中各坐标对应的点,落在如图所示平面直角坐标系阴影区域内的是( )
A. B. C. D.
6.(2023春·湖南益阳·八年级统考期末)下列在具体情境中不能确定平面内位置的是( )
A.东经,北纬 B.电影院某放映厅7排3号
C.益阳大道 D.万达广场北偏东方向,2千米处
7.(2023秋·广西贺州·八年级统考期末)在平面直角坐标系中,将点向右平移2个单位长度后,那么平移后对应的点的坐标是( )
A. B. C. D.
二、填空题
8.(2023秋·浙江湖州·八年级统考期末)如果用表示4排5号,那么6排3号可表示成 .
9.(2023秋·湖南长沙·八年级长沙市开福区青竹湖湘一外国语学校校考期末)在平面直角坐标系中,点到轴的距离为4,则的值为 .
10.(2023春·湖南株洲·八年级株洲市景弘中学校考期末)已知点关于x轴的对称点为,则 .
11.(2023春·山东青岛·八年级统考期末)如图,在平面直角坐标系中,轴上有一点,点第1次向上平移2个单位至点,接着又向左平移2个单位至点,然后再向上平移2个单位至点,向左平移2个单位至点,照此规律平移下去,点平移至点时,点的坐标是 .
三、解答题
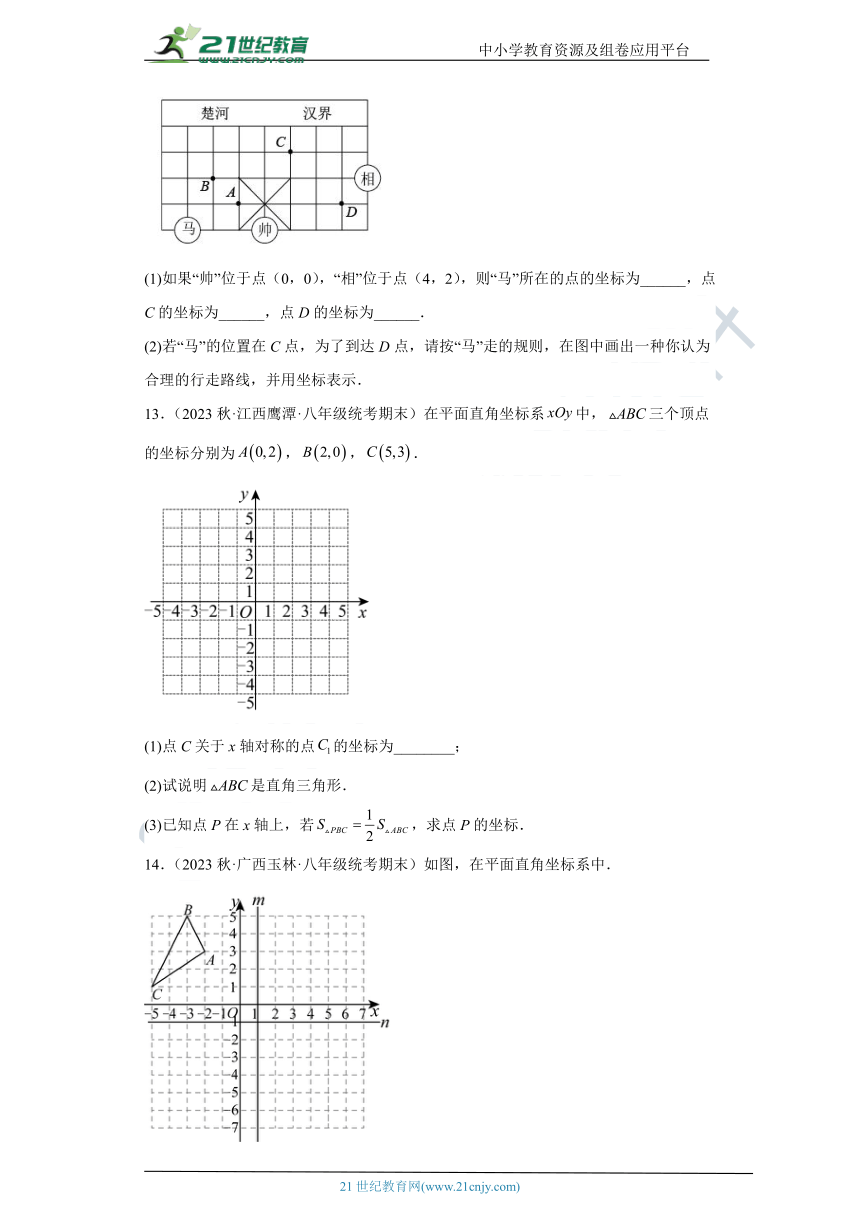
12.(2023秋·甘肃兰州·八年级校联考期末)中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走例如:图中“马”所在的位置可以直接走到点A、B处.
(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,在图中画出一种你认为合理的行走路线,并用坐标表示.
13.(2023秋·江西鹰潭·八年级统考期末)在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)点C关于x轴对称的点的坐标为________;
(2)试说明是直角三角形.
(3)已知点P在x轴上,若,求点P的坐标.
14.(2023秋·广西玉林·八年级统考期末)如图,在平面直角坐标系中.
(1)分别画出关于直线(直线上各点的横坐标都是1)对称的和关于直线(直线上各点的纵坐标都是)对称的;
(2)若上有一点,则关于直线对称后的对应点的坐标为___________,则关于直线对称后的对应点的坐标为___________.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据用有序数对表示位置可进行求解.
【详解】解:由题意得:参加团体操表演的至少有(人),
故选B.
【点睛】本题主要考查平面直角坐标系,熟练掌握利用有序数对表示位置是解题的关键.
2.D
【分析】关于x轴对称横坐标不变,纵坐标变为相反数,直接列出方程解出即可
【详解】解:∵点P(m﹣1,4)与点Q(2,n﹣2)关于x轴对称,
∴m﹣1=2,n﹣2=﹣4,
解得:m=3,n=﹣2,
则mn=3﹣2=.
故选D.
【点睛】考查点关于坐标轴的对称性,基础知识扎实是解题关键
3.A
【分析】根据平面直角坐标系中点的坐标特点,当点的横坐标相同时,线段与y轴平行,与x轴垂直即可解答.
【详解】∵M(3,﹣2),N(3,﹣1),∴横坐标相同,∴MN⊥x轴,故选A.
【点睛】本题考查的是平面直角坐标系中点的坐标规律,熟练掌握与x轴平行,与y轴平行的点的坐标规律是关键.
4.A
【分析】根据题意画出平面直角坐标系即可确定点F的坐标.
【详解】解:根据点E的坐标为,点G的坐标为,画出平面直角坐标系如图,
由坐标系可得点F的坐标为,
故选:A.
【点睛】本题主要考查学生结合图片确定点的坐标的能力,解题的关键是确定坐标原点的位置.
5.A
【分析】分别描出四个选项中点的坐标在坐标系中的位置,然后判断即可.
【详解】解:如图所示,点A(1,2),点B(2,0),点C(0,3),点D(-1,-1),
∴落在阴影区域内的点只有点A(1,2),
故选A.
【点睛】本题主要考查了在坐标系中描点,解题的关键在于能够熟练掌握平面直角坐标系的相关知识.
6.C
【分析】根据确定平面内位置的方法进行判断即可.
【详解】解:A.东经,北纬能确定平面内位置,故选项不符合题意;
B.电影院某放映厅7排3号在具体情境中能确定平面内位置,故选项不符合题意;
C.益阳大道不能确定平面内位置,故选项符合题意;
D.万达广场北偏东方向,2千米处在具体情境中能确定平面内位置,故选项不符合题意.
故选:C.
【点睛】此题考查了平面内位置的确定,熟练掌握平面内位置的确定是解题的关键.
7.A
【分析】根据平移时,点的坐标变化规律“左加右减”进行计算即可解答.
【详解】解:点向右平移2个单位长度后,那么平移后对应的点,
即.
故选:A.
【点睛】本题考查了平移点的坐标变化规律,掌握“左加右减”的性质是解题的关键.
8.
【分析】由“(4,5)表示4排5号”可知,数对中第一个数字表示排,第二个数字表示号,据此即可用数对表示出6排3号.
【详解】解:表示4排5号,则6排3号记作.
故答案为:.
【点睛】此题主要考查了坐标确定位置,关键是根据已知条件确定数对中每个数字所代表的意义.
9.或6
【分析】根据点到轴的距离等于横坐标的绝对值列出方程,然后求解即可.
【详解】解:点到轴的距离为4,
,
解得或6.
故答案为:或6.
【点睛】此题考查的是点的坐标,掌握点的坐标的定义是解决此题的关键.
10.7
【分析】根据关于x轴对称的点横坐标相同,纵坐标互为相反数求出m、n的值即可得到答案.
【详解】解:∵点关于x轴的对称点为,
∴,
∴,
故答案为:7.
【点睛】本题主要考查了坐标与图形变化—轴对称,熟知关于x轴对称的点横坐标相同,纵坐标互为相反数是解题的关键.
11.
【分析】根据题意确定平移规律即可求解.
【详解】解:由题意得:点与点的横坐标相同
点的横坐标比点的横坐标减少:
即点的横坐标为:
∴点的横坐标也为:
而点的纵坐标比点的纵坐标增加:
∴点的纵坐标为:
∴点的坐标是
故答案为:
【点睛】本题考查坐标的规律探索.确定平移规律是解题关键.
12.(1),,
(2)路线见解析,走路线为
【分析】(1)结合图示,确定原点,再根据题意求出点的位置;
(2)结合图示,确定原点,再根据题意求出马走的路线.
【详解】(1)解:∵“帅”位于点(0,0),“相”位于点(4,2),
∴“马”所在的点的坐标为(-3,0),
点C的坐标为(1,3),
点D的坐标为(3,1).
故答案为,,.
(2)解:以 “帅”为(0,0),则“马”走的路线为,
如图:
.
【点睛】本题考查了用有序数对解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置.
13.(1)
(2)是直角三角形,理由见解析
(3)或
【分析】(1)关于x轴对称的两点横坐标相等,纵坐标互为相反数;
(2)利用两点间的距离公式计算出的三边长,利用勾股定理逆定理进行验证即可;
(3)分别表示出即可求出点P的坐标.
【详解】(1)解:由题意得:点的坐标为;
(2)解:∵,,,
∴,
∴是直角三角形;
(3),
设P点坐标为,
∵,
∴,
∴,
∴或,
P点坐标为或.
【点睛】本题综合考查了关于x轴对称的两点的坐标特征、勾股定理的逆定理及三角形的面积表示.熟记相关结论是解题关键.
14.(1)见解析
(2),
【分析】(1)根据轴对称图形的性质即可作出;
(2)根据关于对称轴对称的点与对称轴的距离相等即可求解.
【详解】(1)解:作图如下:
(2)解:若上有一点,
点到直线的距离为,到直线n的距离为,
,,
则关于直线对称后的对应点的坐标为,则关于直线对称后的对应点的坐标为 .
【点睛】本题考查了网格作图、对称点的坐标,关于对称轴对称的点与对称轴的距离相等.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第4章 图形与坐标 单元精选精练 2023-2024学年浙教版八年级数学上册 (含解析)
一、单选题
1.(2023春·湖南株洲·八年级统考期末)小军参加团体操表演,他的位置用数对表示是,如果这时的方队是一个正方形,参加团体操表演的至少有( )人.
A.80 B.64 C.24 D.11
2.(2021春·重庆万州·八年级统考期末)已知点P(m﹣1,4)与点Q(2,n﹣2)关于x轴对称,则mn的值为( )
A.9 B.﹣9 C.﹣ D.
3.(2021秋·福建三明·八年级统考期末)已知点M(3,﹣2),N(3,﹣1),则线段MN与x轴( )
A.垂直 B.平行 C.相交 D.不垂直
4.(2023秋·辽宁锦州·八年级统考期末)如图,若点E的坐标为,点G的坐标为,则点F的坐标为( )
A. B. C. D.
5.(2022秋·浙江温州·八年级统考期末)下列选项中各坐标对应的点,落在如图所示平面直角坐标系阴影区域内的是( )
A. B. C. D.
6.(2023春·湖南益阳·八年级统考期末)下列在具体情境中不能确定平面内位置的是( )
A.东经,北纬 B.电影院某放映厅7排3号
C.益阳大道 D.万达广场北偏东方向,2千米处
7.(2023秋·广西贺州·八年级统考期末)在平面直角坐标系中,将点向右平移2个单位长度后,那么平移后对应的点的坐标是( )
A. B. C. D.
二、填空题
8.(2023秋·浙江湖州·八年级统考期末)如果用表示4排5号,那么6排3号可表示成 .
9.(2023秋·湖南长沙·八年级长沙市开福区青竹湖湘一外国语学校校考期末)在平面直角坐标系中,点到轴的距离为4,则的值为 .
10.(2023春·湖南株洲·八年级株洲市景弘中学校考期末)已知点关于x轴的对称点为,则 .
11.(2023春·山东青岛·八年级统考期末)如图,在平面直角坐标系中,轴上有一点,点第1次向上平移2个单位至点,接着又向左平移2个单位至点,然后再向上平移2个单位至点,向左平移2个单位至点,照此规律平移下去,点平移至点时,点的坐标是 .
三、解答题
12.(2023秋·甘肃兰州·八年级校联考期末)中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走例如:图中“马”所在的位置可以直接走到点A、B处.
(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为______,点C的坐标为______,点D的坐标为______.
(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,在图中画出一种你认为合理的行走路线,并用坐标表示.
13.(2023秋·江西鹰潭·八年级统考期末)在平面直角坐标系中,三个顶点的坐标分别为,,.
(1)点C关于x轴对称的点的坐标为________;
(2)试说明是直角三角形.
(3)已知点P在x轴上,若,求点P的坐标.
14.(2023秋·广西玉林·八年级统考期末)如图,在平面直角坐标系中.
(1)分别画出关于直线(直线上各点的横坐标都是1)对称的和关于直线(直线上各点的纵坐标都是)对称的;
(2)若上有一点,则关于直线对称后的对应点的坐标为___________,则关于直线对称后的对应点的坐标为___________.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.B
【分析】根据用有序数对表示位置可进行求解.
【详解】解:由题意得:参加团体操表演的至少有(人),
故选B.
【点睛】本题主要考查平面直角坐标系,熟练掌握利用有序数对表示位置是解题的关键.
2.D
【分析】关于x轴对称横坐标不变,纵坐标变为相反数,直接列出方程解出即可
【详解】解:∵点P(m﹣1,4)与点Q(2,n﹣2)关于x轴对称,
∴m﹣1=2,n﹣2=﹣4,
解得:m=3,n=﹣2,
则mn=3﹣2=.
故选D.
【点睛】考查点关于坐标轴的对称性,基础知识扎实是解题关键
3.A
【分析】根据平面直角坐标系中点的坐标特点,当点的横坐标相同时,线段与y轴平行,与x轴垂直即可解答.
【详解】∵M(3,﹣2),N(3,﹣1),∴横坐标相同,∴MN⊥x轴,故选A.
【点睛】本题考查的是平面直角坐标系中点的坐标规律,熟练掌握与x轴平行,与y轴平行的点的坐标规律是关键.
4.A
【分析】根据题意画出平面直角坐标系即可确定点F的坐标.
【详解】解:根据点E的坐标为,点G的坐标为,画出平面直角坐标系如图,
由坐标系可得点F的坐标为,
故选:A.
【点睛】本题主要考查学生结合图片确定点的坐标的能力,解题的关键是确定坐标原点的位置.
5.A
【分析】分别描出四个选项中点的坐标在坐标系中的位置,然后判断即可.
【详解】解:如图所示,点A(1,2),点B(2,0),点C(0,3),点D(-1,-1),
∴落在阴影区域内的点只有点A(1,2),
故选A.
【点睛】本题主要考查了在坐标系中描点,解题的关键在于能够熟练掌握平面直角坐标系的相关知识.
6.C
【分析】根据确定平面内位置的方法进行判断即可.
【详解】解:A.东经,北纬能确定平面内位置,故选项不符合题意;
B.电影院某放映厅7排3号在具体情境中能确定平面内位置,故选项不符合题意;
C.益阳大道不能确定平面内位置,故选项符合题意;
D.万达广场北偏东方向,2千米处在具体情境中能确定平面内位置,故选项不符合题意.
故选:C.
【点睛】此题考查了平面内位置的确定,熟练掌握平面内位置的确定是解题的关键.
7.A
【分析】根据平移时,点的坐标变化规律“左加右减”进行计算即可解答.
【详解】解:点向右平移2个单位长度后,那么平移后对应的点,
即.
故选:A.
【点睛】本题考查了平移点的坐标变化规律,掌握“左加右减”的性质是解题的关键.
8.
【分析】由“(4,5)表示4排5号”可知,数对中第一个数字表示排,第二个数字表示号,据此即可用数对表示出6排3号.
【详解】解:表示4排5号,则6排3号记作.
故答案为:.
【点睛】此题主要考查了坐标确定位置,关键是根据已知条件确定数对中每个数字所代表的意义.
9.或6
【分析】根据点到轴的距离等于横坐标的绝对值列出方程,然后求解即可.
【详解】解:点到轴的距离为4,
,
解得或6.
故答案为:或6.
【点睛】此题考查的是点的坐标,掌握点的坐标的定义是解决此题的关键.
10.7
【分析】根据关于x轴对称的点横坐标相同,纵坐标互为相反数求出m、n的值即可得到答案.
【详解】解:∵点关于x轴的对称点为,
∴,
∴,
故答案为:7.
【点睛】本题主要考查了坐标与图形变化—轴对称,熟知关于x轴对称的点横坐标相同,纵坐标互为相反数是解题的关键.
11.
【分析】根据题意确定平移规律即可求解.
【详解】解:由题意得:点与点的横坐标相同
点的横坐标比点的横坐标减少:
即点的横坐标为:
∴点的横坐标也为:
而点的纵坐标比点的纵坐标增加:
∴点的纵坐标为:
∴点的坐标是
故答案为:
【点睛】本题考查坐标的规律探索.确定平移规律是解题关键.
12.(1),,
(2)路线见解析,走路线为
【分析】(1)结合图示,确定原点,再根据题意求出点的位置;
(2)结合图示,确定原点,再根据题意求出马走的路线.
【详解】(1)解:∵“帅”位于点(0,0),“相”位于点(4,2),
∴“马”所在的点的坐标为(-3,0),
点C的坐标为(1,3),
点D的坐标为(3,1).
故答案为,,.
(2)解:以 “帅”为(0,0),则“马”走的路线为,
如图:
.
【点睛】本题考查了用有序数对解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置.
13.(1)
(2)是直角三角形,理由见解析
(3)或
【分析】(1)关于x轴对称的两点横坐标相等,纵坐标互为相反数;
(2)利用两点间的距离公式计算出的三边长,利用勾股定理逆定理进行验证即可;
(3)分别表示出即可求出点P的坐标.
【详解】(1)解:由题意得:点的坐标为;
(2)解:∵,,,
∴,
∴是直角三角形;
(3),
设P点坐标为,
∵,
∴,
∴,
∴或,
P点坐标为或.
【点睛】本题综合考查了关于x轴对称的两点的坐标特征、勾股定理的逆定理及三角形的面积表示.熟记相关结论是解题关键.
14.(1)见解析
(2),
【分析】(1)根据轴对称图形的性质即可作出;
(2)根据关于对称轴对称的点与对称轴的距离相等即可求解.
【详解】(1)解:作图如下:
(2)解:若上有一点,
点到直线的距离为,到直线n的距离为,
,,
则关于直线对称后的对应点的坐标为,则关于直线对称后的对应点的坐标为 .
【点睛】本题考查了网格作图、对称点的坐标,关于对称轴对称的点与对称轴的距离相等.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
